№282. Диденко И. С., Гераськин В. В. Кристаллофизика

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Лабораторная 5

ИНДИЦИРОВАНИЕ КРИСТАЛЛОВ СРЕДНЕЙ И НИЗШЕЙ КАТЕГОРИЙ

5.1. Цель работы

Освоение методов определения индексов плоскостей и направле- ний в кристаллах средней и низшей категорий.

5.2. Теоретическое введение

При индицировании некубических кристаллов необходимо учи- тывать расположение координатных осей (стандартная кристалло- графическая установка) и соотношение единичных параметров по этим осям.

5.2.1. Индицирование кристаллов тетрагональной сингонии

В тетрагональной сингонии за ось Z принимается ось 4 или 4 (единственное единичное направление), за Х и Y – две прямые, сов- падающие с горизонтальными осями симметрии 2 или нормалями к вертикальным плоскостям симметрии, или вдоль ребер кристалла (при отсутствии осей 2 и m). Таким образом, α = β = γ = 90°. Единич- ные параметры по осям Х и Y равны друг другу, так как эти оси яв- ляются симметрично равными, и не равны единичному параметру по оси Z, т.е. a = b ≠ c. Единичная грань отсекает одинаковые отрезки по осям X и Y, а по оси Z отрезок им не равный. При выполнении этих требований несколькими гранями за единичную грань принимается наиболее развитая из них грань.

Гномостереографическая проекция единичной грани тетрагональ ного кристалла обязательно находится на стереографической

ции вертикальной плоскости, делящей угол XOY пополам, за исклю- чением точки, где проектируется грань, отсекающая по всем трем осям отрезки одинаковой длины (рис. 5.1). На рис. 5.1 представлена единичная грань и проекции граней тетрагонального кристалла в случае, когда с < а = b.

61

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

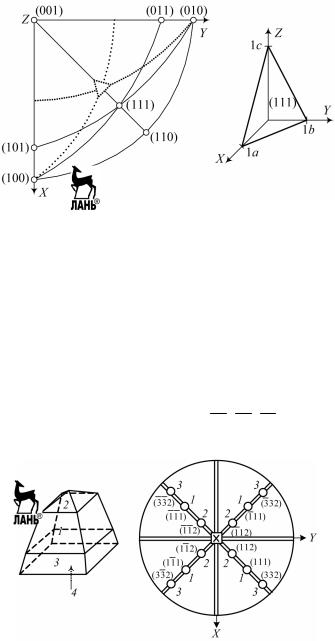
Рис. 5.1. К индицированию кристаллов тетрагональной сингонии

На рис. 5.2 представлен многогранник тетрагональной сингонии. Ес- ли за единичную грань принять наиболее развитую грань 1 (тетраго- нальная пирамида) и если она отсекает по координатным осям отрезки 30, 30 и 40 мм, то соотношение единичных параметров a : b : c = 3 : 3 : 4. Если грань другой тетрагональной пирамиды (грань 2) отсекает по осям

шение к целым числам, получим индексы Миллера граней 2: {112}. Если грань третьей тетрагональной пирамиды (грань 3) отсекает по

осям отрезки 25, 25 и 50 мм, то h : k : l = 3 : 3 : 4 . Таким образом,

25 25 50

грани 3 имеют индексы {332}.

Рис. 5.2. Многогранник тетрагональной сингонии, проекции его граней и элементов симметрии

62

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Если единичная грань отсутствует, то вследствие того, что в тет- рагональной сингонии a = b, при индицировании для нахождения

5.2.2.Индицирование кристаллов ромбической сингонии

За кристаллографические оси в кристаллах ромбической сингонии принимаются три единичных направления, которые совпадают с осями симметрии 2 или нормалями к плоскостям симметрии. Обычно за ось Z принимается ось наиболее развитой зоны; с другой стороны, кристалл желательно устанавливать так, чтобы имелась единичная грань.

У ромбических кристаллов α = β = γ = 90° и a ≠ b ≠ c. Следова- тельно, единичная грань отсекает по всем трем осям отрезки различ- ной длины и ее гномостереографическая проекция находится внутри круга проекций, но только не на месте стереографических проекций плоскостей, делящих пополам двугранные углы между координат- ными плоскостями (рис. 5.3). На рис. 5.3 представлена единичная грань и проекции граней ромбического кристалла в случае, когда

а < b < c.

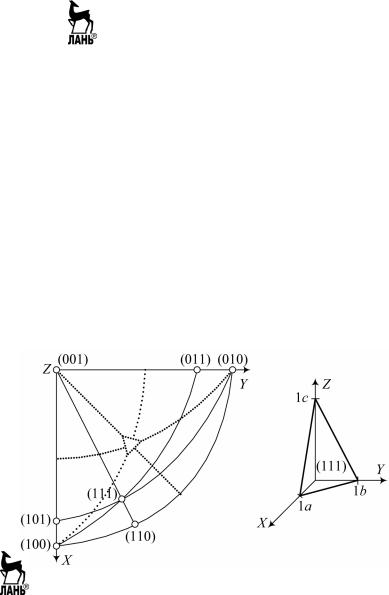
Рис. 5.3. К индицированию кристаллов ромбической сингонии

На рис. 5.4 представлен многогранник ромбической сингонии. Примем за единичную грань – 1 (ромбическая пирамида), так как она

63

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

отсекает отрезки по всем трем координатным осям и больше по пло- щади, чем грань 2, удовлетворяющая тому же условию. Единичная грань отсекает по осям координат отрезки 30, 40 и 50 мм, тогда соот- ношение единичных параметров a : b : c = 3 : 4 : 5. Если грань другой ромбической пирамиды – грань 2 – отсекает по осям отрезки 30, 40 и

дексы {112}.

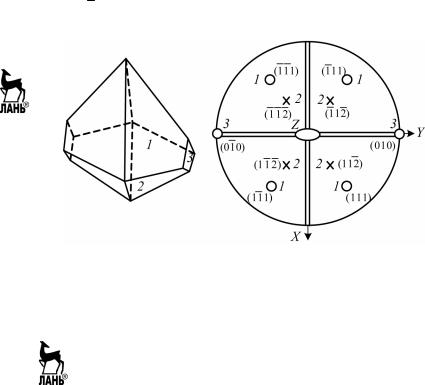
Рис. 5.4. Многогранник ромбической сингонии, проекции его граней и элементов симметрии

5.2.3.Индицирование кристаллов моноклинной

итриклинной сингоний

моноклинных кристаллов за ось Y (горизонтальная ось) прини- ось симметрии 2 (или направление нормали к плоскости сим- метрии). За ось Z выбирается ось наиболее развитой зоны (Z – верти- кальная ось). Ось X параллельна действительным или возможным ребрам кристалла и выбирается так, что плоскость ХОZ перпендику- лярна оси Y, и, таким образом, β ≠ α = γ = 90°. Единичные параметры не равны по всем трем осям (a ≠ b ≠ c), и индицирование проводится аналогично индицированию граней кристаллов ромбической синго-

нии с учетом того, что β ≠ 90°.

У кристаллов триклинной сингонии координатные оси выбирают- ся параллельно ребрам кристалла. Ось Z располагается вертикально, а углы между координатными осями не равны 90°. Единичные пара-

64

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

метры не равны по всем трем осям, и индицирование граней кри- сталлов проводится аналогично индицированию кристаллов ромби- ческой сингонии с учетом того, что α ≠ β ≠ γ ≠ 90°.

5.2.4.Индицирование кристаллов тригональной

игексагональной сингоний

Главное отличие гексагональной и тригональной сингоний рас- смотренных выше состоит в том, что кристаллографические оси X и Y не расположены под углом 90° друг к другу. Индицирование кри- сталлов гексагональной и тригональной сингоний проводится в гек- сагональной установке кристаллографической системы координат: a = b ≠ c, α = β = 90°, γ = 120°. Таким образом, кристаллографические оси X и Y расположены под 120° друг к другу.

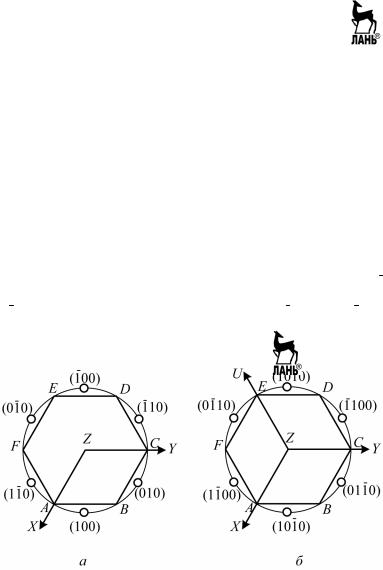
Проиндицируем грани гексагональной призмы (рис. 5.5, а). Тре- тий индекс у всех граней равен нулю, так как они параллельны оси Z. Грани АВ и DE параллельны оси Y, т.е. для них индекс k = 0; грани ВС и EF параллельны оси X, т.е. для них индекс h = 0; грани CD и FA отсекают одинаковые отрезки на осях X и Y в их отрицательных либо положительных направлениях. Все шесть граней принадлежат одной простой форме – гексагональной призме, однако обладают разными

наборами индексов в символе: грани AB (100), BC (010) , DE (100) ,

EF (010) – два «ноля» и «единица», а грани CD (110) , FA (110) – две

«единицы» и «ноль».

Рис. 5.5. Индицирование гексагональных и тригональных кристаллов

65

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Для удобства формально вводится четвертая ось координат – ось U. Она лежит в плоскости осей X и Y; (XOU) = (YOU) = 120° (рис. 5.5, б). Появляется четвертый индекс – i, соответствующий оси U, который записывается в символе на третьем месте. Таким образом, для кри- сталлов гексагональной и тригональной сингоний (в гексагональной установке) символ состоит из четырех цифр hkil). При такой «че- тырехиндексной» записи грани гексагональной призмы (рис. 5.5, б) будут иметь символы, состоящие из двух нолей и двух единиц: AB

(1010), BC (0110), СD (1100), DE (1010), EF (0110), FA (1100).

Оси координат X, Y и U лежат в одной плоскости, следовательно, не являются независимыми. Соответствующие индексы h, k и i – за- висимы и связаны соотношением

Таким образом, сумма первых трех индексов грани кристалла гек- сагональной или тригональной сингонии равна нулю. Отсюда следу- ет, что нет необходимости искать каждый из первых трех индексов: достаточно определить два любых, а третий вычислить.

Чтобы перейти от «четырехиндексной» записи к «трехиндексной»,

достаточно удалить из символа третий индекс i: (0110) → (010). Что-

бы перейти от «трехиндексной записи к «четырехиндексной», необ- ходимо вычислить индекс i, используя формулу (5.1): i = – (h + k).

Тогда (122) → (1232) .

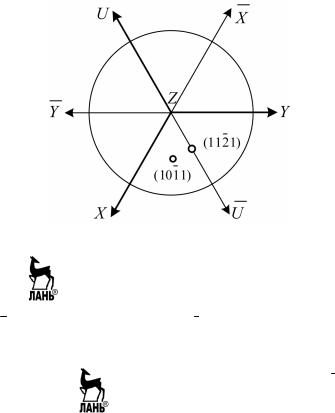
Индексы Миллера единичной грани в гексагональных и триго- нальных кристаллах отличаются от всех остальных сингоний. Благо- даря «четырехиндексной» записи символ единичной грани не может состоять из четырех единиц. Единичная грань в этих сингониях име-

ет две установки (рис. 5.6). Первая – (1121) – отсекает единичные

отрезки по «исходным» осям координат X, Y и Z, а по «вспомога- тельной» оси U отсекает отрезок –0,5а. Эта установка более очевид- на, так как отбросив «дополнительный» индекс i по оси U, получим символ единичной грани (111). Вторая установка единичной грани

имеет символ (1011) и отсекает единичные отрезки по осям X, Z, от-

рицательной части оси U, и параллельна оси Y.

66

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Рис. 5.6. Два возможных положения единичной грани кристаллах гексагональной и тригональной сингоний

Некоторые многогранники, например, гексагональную пирамиду (см. рис. 2.7, в), можно установить двумя способами: с единичной гра-

нью (1121) и с единичной гранью (1011). А, например, тригональная

пирамида (рис. 2.7, а) по правилам расположения элементов симметрии относительно осей координат (см. лабораторную работу 2) может быть

установлена только способом – с единичной гранью (1011).

5.2.5. Определение символов граней кристалла по методу косинусов

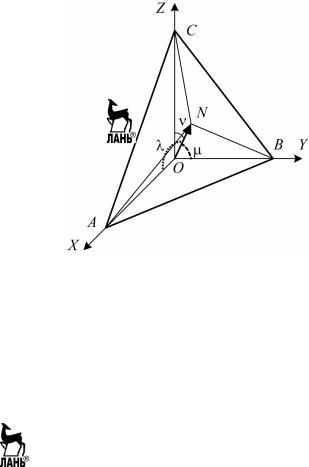
Если известны углы между нормалью к грани N и осями коорди- нат X, Y и Z, то индексы Миллера можно рассчитать по методу коси- нусов. Рассмотрим его на примере ортогональной системы коорди-

нат (рис. 5.7).

Плоскость (грань кристалла) ABC пересекает координатные оси X, Y и Z в точках A, B и C соответственно и отсекает на них отрезки OA, OB и OC. Восстановим нормаль ON к грани ABC из начала координат О. Она составляет с осями координат следующие углы: λ = (AON),

67

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Рис. 5.7. Схема к определению символов граней кристалла по методу косинусов

С другой стороны, отрезки, отсекаемые гранью на осях координат (ребрах кристалла), составляют целое число единичных параметров (осевых единиц) a, b, c:

где r, s, t – целые числа.

Миллера h, k, l относятся как величины, обратные отрез- кам, отсекаемым гранью на координатных осях (отрезки выражены в осевых единицах). С учетом этого получим

Отсюда получаем соотношение между индексами Миллера грани и ее направляющими косинусами:

Для кубической сингонии это выражение выглядит проще, так как a = b = c:

68

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

В гексагональной и тригональной сингониях

a

где ε – угол между координатной осью U и нормалью к грани.

Для кристаллов средней категории это выражение тоже упрощается:

Таким образом, чтобы определить индексы Миллера грани (hkl), необходимо вычислить косинусы углов λ, μ, ν и привести их соот- ношение к взаимно простым целым числам.

5.3. Методика индицирования кристаллов средней и низшей категорий

После установки кристалла выделяем единичную грань (если та- кая имеется) и определяем соотношение единичных параметров по координатным осям. Для определения индекса любой грани необхо- димо определить отрезки, отсекаемые данной гранью по координат- ным осям, выраженные в единичных параметрах, и взять их обратное отношение.

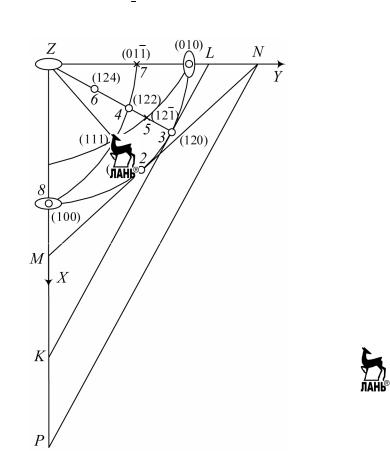
При индицировании граней кристалла любой сингонии, когда нам известны величины α, β, γ и соотношение между a, b, c, представле- ние о символах граней нетрудно составить по их проекциям. На рис. 5.8 изображены гномостереографические проекции нескольких гра- ней кристалла ромбической сингонии. За кристаллографические оси приняты оси симметрии второго порядка. Примем за единичную грань 1, ее символ (111). Грань 2 имеет символ (110) так как она так же как и единичная грань пересекает плоскость проекций по линии, параллельной касательной к кругу проекций МN. Грани 3, 4, 5 и 6 пересекают плоскость проекций по линиям параллельным KL. Если касательную KL перенести параллельно она проходила через точку N (линия NР), то можно оценить первые два индекса верти- кальной грани 3: (120) – из соотношения отрезков ОР и ОМ.

Если нам известно, что грань 8 имеет символ (100), как парал-

лельная двум координатным осям, а грань 7 – символ (011) , то

грань 4 будет иметь символ (122), так как соотношение первых ин- дексов должно быть 1 : 2 (таково соотношение у всех граней 3, 4, 5 и

69

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

6), а второй и третий индекс равны (у всех граней 1, 4, 7 и 8). Если после параллельного переноса грани 3, 4, 5 и 6 будут проходить че- рез точки K и L и при этом отрезок, отсекаемый по оси Z гранью 4, будет в два раза меньше, чем отрезок, отсекаемый гранью 5, и в два раза больше, чем отрезок, отсекаемый по оси Z гранью 6, то индекс

грани 6 – (124), а грани 5 – (121) .

О

Рис. 5.8. Гномостереографические проекции граней ромбического кристалла (симметрия 222). Показана четверть круга проекций

5.4.Порядок выполнения работы

1.Определить элементы симметрии кристаллического многогран- ника и построить их стереографическую проекцию с верхней полу- сферы.

70