№282. Диденко И. С., Гераськин В. В. Кристаллофизика

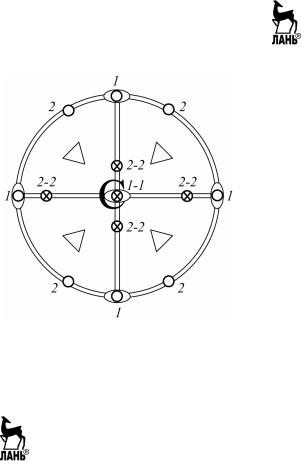
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

го порядка попадает в центр круга проекций, две другие оси L2, яв- ляющиеся горизонтальными направлениями, проектируются на ок- ружности круга проекций. Четыре оси симметрии третьего порядка, одинаково наклоненные к осям L2, проектируются в центрах октан- тов круга проекций.

Из трех взаимно перпендикулярных плоскостей симметрии две являются вертикальными и изображаются в виде двух взаимно пер- пендикулярных диаметров круга проекций, очерченных двойными линиями. Горизонтальная плоскость симметрии изобразится как ок- ружность круга проекций. Наличие центра симметрии показываем буквой С у центра круга проекций (рис. 3.9).

Рис. 3.9. Стереографическая проекция элементов симметрии пирита и гномостереографические проекции его граней

4. Строим гномостереографические проекции граней кристалла. Построение гномостереографических проекций граней кристалла ведется относительно его элементов симметрии. Так как нормали к граням 1 совпадают с осями второго порядка, то проекции этих гра- ней попадут в выходы этих осей. В центре круга проекций располо- жатся проекции двух горизонтальных граней – верхней и нижней: верхнюю обозначаем кружочком, а нижнюю обозначаем крестиком и проставляем около проекций номера соответствующих граней. Про- екции остальных четырех вертикальных граней 1 расположатся на окружности круга проекций также в выходах осей L2 (см. рис. 3.9).

41

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Нормали к граням 2 лежат в плоскостях симметрии, при этом все верхние и нижние грани 2 оказываются связанными горизонтальной плоскостью симметрии.

5. Комбинационный многогранник пирита образован двумя просты- ми формами: гексаэдром (грани 1) и пентагондодекаэдром (грани 2).

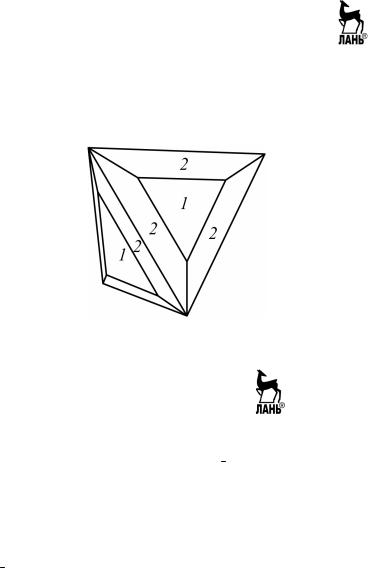
Пример 3.2. Построить стереографическую проекцию элементов симметрии и гномостереографические проекции граней сфалерита ZnS (цинковая обманка), модель которого изображена на рис. 3.10.

Рис. 3.10. Кристалл сфалерита

1. Кристалл сфалерита обладает тремя инверсионными осями чет- вертого порядка, проходящими через середины противоположных ребер, по которым пересекаются грани 2, четырьмя осями третьего порядка, проходящими через середины граней 1 и вершины, в кото- рых сходятся грани 2, а также шестью плоскостями симметрии, рас- положенными так, что каждая из осей L4 служит линией пересече-

ния двух взаимно перпендикулярных плоскостей.

2.Выберем три взаимно ортогональные инверсионные оси чет- вертого порядка в качестве координатных осей.

3.Строим стереографическую проекцию элементов симметрии. Стереографические проекции вертикальной и двух горизонтальных

осей L4 займут положение в центре круга проекций и на окружности

круга проекций соответственно. Проекции четырех осей L3 будут располагаться в центрах четырех октантов круга проекций. Две вер- тикальные плоскости симметрии изображаются в виде диаметров круга проекций, а четыре наклонные плоскости симметрии – в виде дуг, опирающихся на диаметры круга проекций (рис. 3.11).

42

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Рис. 3.11. Стереографическая проекция элементов симметрии кристалла сфалерита и гномостереографические проекции его граней

4.Строим гномостереографические проекции граней сфалерита. Нормали к граням 1 совпадают с выходами осей третьего порядка, при этом верхние и нижние грани чередуются друг с другом. Норма- ли к граням 2 лежат в плоскостях симметрии кристалла, симметрич- но располагаясь вокруг осей L3.

5.Комбинационный многогранник кристалла сфалерита образо- ван двумя простыми формами – тетраэдром (грани 1) и тригонтри- тетраэдром (грани 2).

3.5. Требования к отчету

Отчет о работе должен содержать:

1)класс симметрии модели кристаллического многогранника (за- писанный в учебной и интернациональной символике);

2)правила выбора кристаллографических осей и ориентации мно- гогранника кубической сингонии;

3)стереографическую проекцию всех элементов симметрии модели;

4)гномостереографические проекции граней модели с указанием простых форм.

Литература

Розин К.М., Петраков В.С. Кристаллофизика: Учеб. пособие. –

М.: МИСиС, 2006. – 249 с.

Розин К.М. Практическая кристаллография. – М.: МИСиС, 2005. – 487 с.

43

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Контрольные вопросы

1.Наличие каких элементов симметрии характерно для кристал- лов кубической сингонии?

2.Как выбираются кристаллографические оси в кристаллах куби- ческой сингонии?

3.Где расположены стереографические проекции осей четвертого порядка в кристаллах кубической сингонии?

4.Где расположены стереографические проекции осей третьего порядка в кристаллах кубической сингонии?

5.Какие простые формы кубических кристаллов относятся к ис- ходным?

6.Где расположены гномостереографические проекции граней октаэдра?

7.Где расположены гномостереографические проекции граней гексаэдра?

8.Где расположены гномостереографические проекции граней тетраэдра?

9.Где расположены гномостереографические проекции граней ромбододекаэдра?

10.Где расположены гномостереографические проекции граней пентагондодекаэдра?

44

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Лабораторная работа 4

ИНДИЦИРОВАНИЕ КРИСТАЛЛОВ КУБИЧЕСКОЙ СИНГОНИИ

4.1.Цель работы

1.Освоение метода определения индексов Миллера плоскостей в кристаллах кубической сингонии.

2.Освоение метода определения индексов направлений в кри- сталлах кубической сингонии.

4.2.Теоретическое введение

4.2.1.Индицирование плоскостей (граней кристалла)

Индицирование кристаллов основано на законе рациональности параметров (законе целых чисел) Р.Ж. Гаюи, который показывает, что расположение всех наблюдающихся на кристаллах данного ве- щества граней можно характеризовать некоторыми целыми числами, находящимися между собой в рациональных отношениях.

Закон Гаюи гласит: двойные отношения отрезков, отсекаемых двумя любыми гранями кристалла на трех его пересекающихся реб- рах, равны отношению целых и сравнительно малых чисел.

Если направления трех ребер кристалла принять в качестве коор- динатных осей X, Y и Z (рис. 4.1), то отрезки, отсекаемые на них лю- бой гранью кристалла (ОА1, ОА2, ОВ1 и т.д.), называются парамет-

Рассматриваемые отношения являются отношением целых срав- нительно небольших чисел вследствие того, что ребра кристалла яв- ляются рядами пространственной решетки, а грани кристалла – пло- скими сетками с высокой ретикулярной плотностью.

45

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Рис. 4.1. К закону рациональности параметров

Параметры одной из граней, пересекающей все три оси координат, могут быть приняты за единицы измерения по соответствующим осям и названы единичными параметрами (отрезками) a, b, c, а такая грань – единичной гранью. Тогда положение любой грани кристалла может быть выражено через отрезки pa, qb, rc, где p, q, r – целые положитель- ные или отрицательные числа. Таким образом, в методе параметров (методе Вейса) для определения пространственного положения плоско- сти (грани) используются три параметра p, q, r (параметры Вейса). Они представляют собой измеренные с помощью единичных параметров a, b, c отрезки, отсекаемые данной плоскостью на осях координат.

Абсолютные значения единичных параметров a, b, c не могут быть определены по внешней форме многогранника, но после выбора кон- кретной единичной грани можно определить параметры Вейса p, q, r для любой грани (p, q, r выражены в единичных параметрах a, b, c). Три числа, входящие в тройку параметров, являются взаимно простыми и определяют положение параллельных плоскостей. Обозначение гра- ней кристалла и плоскостей решетки с помощью параметров Вейса является точным и простым, но оказывается неудобным при обозначе- нии граней, параллельных координатным направлениям. Например, грань, перпендикулярная оси Z в кубическом кристалле, имела бы сим- вол ∞ ∞ 1, т.е. пришлось бы привлекать символ «бесконечность».

Современные кристаллографы для описания взаимного располо- жения граней кристалла и плоскостей решетки чаще используются так называемые индексы Миллера. Они представляют собой тройку

46

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Индексы Миллера – величины, обратно пропорциональные от- резкам (выраженным в единичных параметрах а, b, с), которые грань отсекает на трех координатных осях, приведенные к взаимно про- стым целым числам и заключенные в круглые скобки – (hkl).

Индексы грани не отделяются друг от друга никакими знаками, знак «минус» располагается над соответствующим индексом, напри-

мер (110), ( 021 ). Таким образом, индексы Миллера определяют по- ложение параллельных граней (плоскостей структуры), расположен- ных по одну сторону от начала координат.

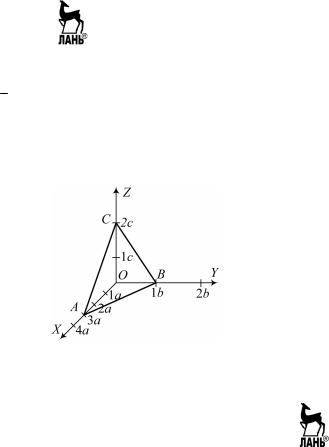
Пример 4.1. Определим индексы Миллера для плоскости АВС на рис. 4.2.

Рис. 4.2. К определению индексов Миллера грани

Для удобства составим табл. 4.1

_______

* При переходе от шага 4 к шагу 5 приводим числа к общему знаменателю и от- брасываем его.

Таким образом, символ грани ABC – (263).

47

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Пример 4.2. Определим символ грани, перпендикулярной оси Z

(рис. 4.3).

Рис. 4.3. К определению индексов Миллера грани, перпендикулярной оси Z

Таблица 4.2

Определение индексов Миллера грани, перпендикулярной оси Z

Таким образом, символ грани – (001).

Итак, для определения символа грани необходимо:

1)определить сингонию кристалла и провести его установку;

2)определить единичные параметры a, b, c, выбрав единичную грань;

3)измерить единичными параметрами отрезки, отсекаемые дан- ной гранью на осях;

4)взять отношение обратных величин этих отрезков и, если нуж- но, преобразовать его в отношение целых взаимно простых чисел.

,что символы всех граней кристалла, принадлежащих к одной простой форме, являются однотипными, т.е. определяются од- ним и тем же набором чисел (индексов) в символе, а символ в этом случае заключается в фигурные скобки. Например, символ каждой из

шести граней куба – (001), (010), (100), (001) , (010) , (100) – содер-

жит два «ноля» и единицу, отличия состоят лишь в смене знаков и перестановке индексов; грани этой простой формы могут быть обо- значены как {100}.

48

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Кроме того, между положением грани и ее индексами можно вы- делить следующие важные закономерности:

1)если грань отсекает по какой-то оси отрезок больший (в еди- ничных параметрах), чем по другой, то индекс грани, соответствую- щей этой оси меньше, чем индекс, соответствующий другой оси (и наоборот);

2)если грань параллельна кристаллографической оси, то индекс грани, соответствующий этой оси, равен нулю;

3)если грань пересекает отрицательный конец оси, то ее параметр по этой оси отрицателен, индекс также отрицательный и над ним ставится знак «минус»;

4)символ грани отражает ее наклон к кристаллографическим осям от- носительно единичной грани, но не отражает расстояние грани от начала координат. Параллельный перенос грани (без пересечения начала коор- динат) равносилен умножению на одно и то же число всех отрезков, от- секаемых гранью на координатных осях, и не влияет на ее символ;

5)Если в индексах двух граней все цифры равны, но имеют различ- ные знаки, это означает, что эти грани параллельны и расположены по

разные стороны от начала координат, например, (123 )

В кубической сингонии координатные оси X, Y, Z направлены вдоль осей четвертого порядка или вдоль осей второго порядка (при отсутст-

вии 4 и 4 ) и углы между ними равны 90°. Единичные параметры равны между собой и поэтому единичная грань в кубических кристаллах отсе- кает на координатных осях равные по длине отрезки. Вследствие этого при индицировании в кубических кристаллах отрезки, отсекаемые на координатных осях, необязательно выражать в осевых единицах, а можно непосредственно находить отношение их величин. Подчеркнем, что такая ситуация характерна только для кубических кристаллов.

Определим местоположение единичной грани. Отметим, что не у всякого кубического кристалла имеется единичная грань. Единичная грань присутствует только у двух простых форм кубической синго- нии – тетраэдра и октаэдра (рис. 4.4 и 4.5), а, например, у куба ее нет.

Однако в кубическом кристалле расположение единичной грани все- гда известно – она перпендикулярна оси третьего порядка; именно так расположенная грань отсекает равные отрезки по трем координатным осям. Следовательно, проекция грани (111) совпадает с проекцией оси L3 в первом октанте круга проекций. Таким образом, даже если у кристалла кубической сингонии нет единичной грани, мы всегда знаем, где была бы ее проекция, если бы у многогранника такая грань присутствовала.

49

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

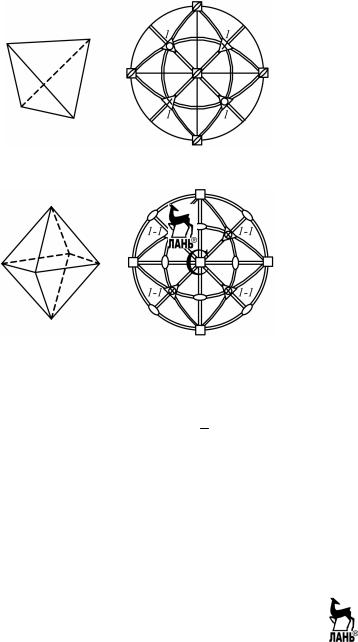
Рис. 4.4. Тетраэдр и проекции его граней и элементов симметрии

Рис. 4.5. Октаэдр и проекции его граней и элементов симметрии

В зависимости от положения граней относительно кристаллографи- ческих осей их символы можно разделить на следующие шесть типов:

1. Единичная грань (см. рис. 4.4 и 4.5). Отрезки, отсекаемые ею на

осях, приняты за единицу. Символы: (111), ( 111 ) и т.д.

2.Грань пересекает одну координатную ось, а двум другим параллельна (в кубической сингонии – грани куба). Символы: (100), (010), (010) и т.д.

3.Грань параллельна одной кристаллографической оси, а по двум другим осям отсекает равное число единичных параметров (в куби- ческой сингонии равные отрезки), грани ромбододекаэдра, (рис. 4.6).

Символы: (110), (101), (011) и т.д.

4.Грань параллельна одной кристаллографической оси, а по двум дру- гим осям отсекает неравные отрезки (в кубической сингонии, например, грани пентагондодекаэдра, рис. 4.7). Символы: (hk0) (h0l), (0kl) и т.д.

5.Грань пересекает три координатные оси, причем по двум из отсекает равное число единичных параметров (в кубической сингонии например, грани тригонтритетраэдра и тетрагонтритетраэдра рис. Символы: (hhl), (hkk) и т.д.

Необходимо различать символы (hhl), где h > l и l > h.

50