№282. Диденко И. С., Гераськин В. В. Кристаллофизика

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

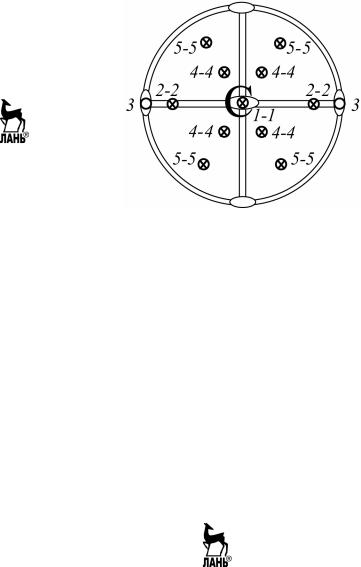
Рис. 2.16. Кристалл серы

1.Рассматриваемый кристалл имеет три оси L2, три плоскости симметрии Р и центр симметрии С. Таким образом, полная совокуп- ность элементов симметрии кристалла 3L23PC (mmm). Кристалл при- надлежит к ромбической сингонии.

2.Координатные оси X, Y, Z совпадают с тремя взаимно перпен- дикулярными осями L2. Ось Z вертикальна.

3.Строим стереографическую проекцию элементов симметрии. Очевидно, что проекция вертикальной оси второго порядка попадает

вцентр круга проекций. Выходы двух других осей L2, являющихся горизонтальными направлениями, проектируются на окружности круга проекций. Из трех взаимно перпендикулярных плоскостей симметрии две являются вертикальными и изображаются в виде двух взаимно перпендикулярных диаметров круга проекций, очерченных двойными линиями. Горизонтальная плоскость симметрии изобра- зится как окружность круга проекций, также очерченная двойной линией. Наличие центра симметрии показываем буквой С в центре круга проекций (рис. 2.17).

4.Строим гномостереографические проекции граней многогран- ника. Построение гномостереографической проекции граней кри- сталла всегда ведется относительно его элементов симметрии. Так как нормали к граням 1 и 3 совпадают с осями второго порядка, сов- падающими с осями координат Z и Y, то проекции этих граней попа- дут на выходы этих осей. В центре круга проекций расположатся проекции двух горизонтальных граней 1 – верхней и нижней; верх- нюю обозначаем кружочком, нижнюю крестиком. Проекции верти- кальных граней 3 расположатся на круге проекций также в выходах

оси L2.

31

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

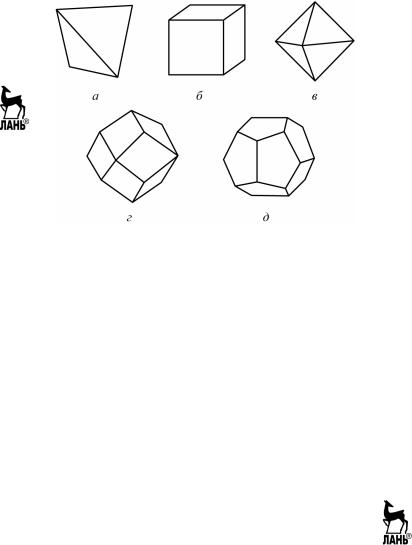
Рис. 2.17. Стереографическая проекция элементов симметрии кристалла серы и гномостереографические проекции его граней

Нормали к граням 2 лежат в плоскости симметрии, при этом верхние и нижние грани 2 оказываются связанными горизонтальной плоскостью симметрии. Проекции граней 4 и 5 находятся внутри круга проекций вне элементов симметрии многогранника.

5. Рассмотрим простые формы. Комбинационный многогранник кристалла серы образован тремя типами простых форм – пинакоида- ми, ромбической призмой и ромбическими дипирамидами. Число про- стых форм равно пяти: два пинакоида (грани 1, 3), ромбическая призма (грани 2), две ромбические дипирамиды (грани 4, 5) (см. рис. 2.16).

2.5. Требования к отчету

Отчет о работе должен содержать:

1)запись класса симметрии модели кристаллического многогран- ника (в учебной и интернациональной символике) и его сингонию;

2)аргументацию выбора кристаллографических осей координат и

3)стереографическую проекцию всех элементов симметрии модели;

4)гномостереографическую проекцию граней кристаллического многогранника с указанием простых форм.

Литература

Розин К.М., Петраков В.С. Кристаллофизика: Учеб. пособие. –

М.: МИСиС, 2006. – 249 с.

32

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Розин К.М. Практическая кристаллография. – М.: МИСиС, 2005. – 487 с.

Контрольные вопросы

1.Объясните принцип построения стереографических проекций направления и плоскости. Как выглядят стереографические проекции направления и плоскости?

2.Где располагаются стереографические проекции направлений: наклонного, вертикального, горизонтального, близкого к вертикаль- ному, близкого к горизонтальному?

3.Как выглядят стереографические проекции плоскостей: на- клонной, вертикальной, горизонтальной?

4.Объясните принцип построения гномостереографической про- екции направления и плоскости.

5.Где располагаются гномостереографические проекции горизон- тальных граней, вертикальных граней, наклонных граней?

6.Как связаны между собой угол между нормалями к граням и yгол между гранями?

7.Что называется пpoстой формой и комбинацией простых форм?

8.Как выбираются кристаллографические оси в кристаллах низ- шей и средней категории? Как они располагаются относительно плоскости чертежа, наблюдателя, элементов симметрии многогран- ника? Каково соотношение между осевыми углами в различных син- гониях?

9.В чем отличие между числом типов простых форм и числом простых форм в комбинации?

33

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Лабораторная работа 3

ПРОЕКТИРОВАНИЕ МОДЕЛЕЙ КРИСТАЛЛИЧЕСКИХ МНОГОГРАННИКОВ КУБИЧЕСКОЙ СИНГОНИИ

3.1. Цель работы

Построение стереографических проекций элементов симметрии моделей кристаллических многогранников кубической сингонии и гномостереографических проекций их граней.

3.2. Теоретическое введение

Простые формы кубической сингонии

Простые формы кубической сингонии характерны только для нее. Ни одна из форм низшей и средней категории, рассмотренных выше, не встречается в кристаллах кубической сингонии. Все 15 простых форм кристаллов кубической сингонии являются закрытыми.

Рассмотрим пять исходных форм, из которых путем усложнения (разбиения граней) могут быть получены остальные простые формы. В названиях этих простых форм указано число граней данного мно- гогранника.

1. Тетраэдр – четыре грани, которые образуют замкнутый объем, форма грани – равносторонний треугольник (в отличие от встречав- шихся ранее ромбического и тетрагонального тетраэдров). Кроме того, все три центральные сечения тетраэдра, перпендикулярные осям L4 , представляют собой квадраты (рис. 3.1, а).

2.Гексаэдр (куб) – шесть граней, их форма – квадрат (рис. 3.1, б).

3.Октаэдр – восемь граней, их форма – равносторонний тре- угольник (рис. 3.1, в).

Следующие два многогранника содержат одинаковое количество граней – 12. Соответственно в названиях обоих простых форм вторая часть – «додекаэдр», а первая часть указывает на форму грани.

4.Ромбододекаэдр – двенадцатигранник, форма грани – ромб

(рис. 3.1, г).

34

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

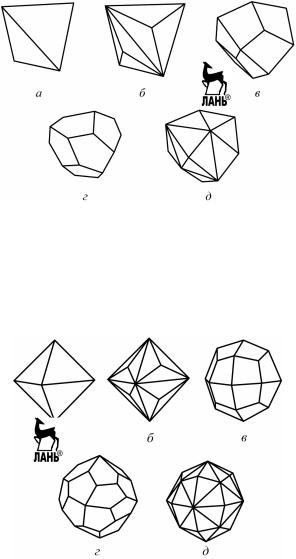
Рис. 3.1. Простые формы кристаллов кубической сингонии: тетраэдр (а); гексаэдр (б); октаэдр (в); ромбододекаэдр (г); пентагондодекаэдр (д)

5.Пентагондодекаэдр – двенадцатигранник, форма грани – пяти- угольник (пентагон) (рис. 3.1, д).

Остальные 10 простых форм кристаллов кубической сингонии мож- но получить из рассмотренных выше. Названия исходной простой фор- мы положены в основу названий производных простых форм.

Если утроить каждую грань тетраэдра, то получим тритетраэдр, т.е. тетраэдр, у которого на месте каждой грани теперь оказалось три. Оказывается, сделать это можно тремя способами и получить соответ- ственно три новые простые формы – двенадцатигранники с различной формой грани, на что указывает первая часть названия (рис. 3.2).

6.Тригонтритетраэдр: форма грани – равнобедренный тре- угольник (рис. 3.2, б).

7.Тетрагонтритетраэдр: форма грани – четырехугольник (рис. 3.2, в).

9. Гексатетраэдр – 24-гранник, форма грани – треугольник (рис. 3.2, д). Аналогично, производными простыми формами от октаэдра (рис. 3.3, а)

являются приведенные ниже.

10. Тригонтриоктаэдр: 24 грани, форма грани – равнобедренный треугольник (рис. 3.3, б).

11. Тетрагонтриоктаэдр: 24 грани, форма грани – четырех- угольник (рис. 3.3, в).

35

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Рис. 3.2. Простые формы кубической сингонии: тетраэдр (а) и его производные – тригонтритетраэдр (б); тетрагонтритетраэдр (в); пентагонтритетраэдр (г); гексатетраэдр (д)

12.Пентагонтриоктаэдр: 24 грани, форма грани – пятиугольник

(рис. 3.3, г).

13.Гексаоктаэдр: 48 граней, форма грани – треугольник (рис. 3.3, д).

Рис. 3.3. Простые формы кубической сингонии: октаэдр (а) и его производные – тригонтриоктаэдр (б); тетрагонтриоктаэдр (в); пентагонтриоктаэдр (г); гексаоктаэдр (д)

Отметим, что гексаоктаэдр обладает наибольшим количеством граней, возможных для простых форм кристаллических многогран- ников; второе название гексаоктаэдра – 48-гранник.

36

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Если на каждой грани куба надстроить четырехгранную пирамид- ку, т.е. из одной грани куба сделать четыре, то получим фигуру, при- веденную ниже.

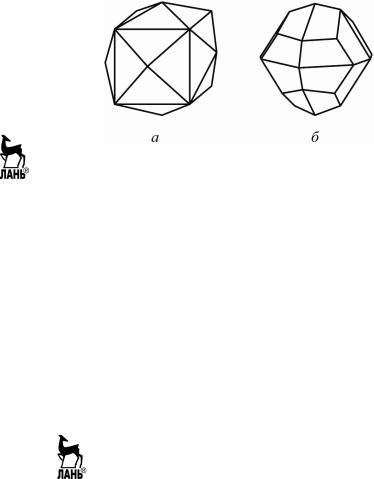
14.Тетрагексаэдр: 24 грани, форма грани – равнобедренный тре- угольник (рис. 3.4, а).

Удваивая каждую грань пентагондодекаэдра, получим фигуру, приведенную ниже

15.Дидодекаэдр: 24 грани, форма грани – четырехугольник (рис. 3.4, б).

Рис. 3.4. Простые формы кубической сингонии: терагексаэдр (а); дидодекаэдр (б)

Отметим, что тетраэдр в кубической сингонии единственный че- тырехгранник, гексаэдр – единственный шестигранник, октаэдр – единственный восьмигранник.

3.3. Методика проектирования моделей кристаллических многогранников кубической сингонии

Характерным признаком кристаллов кубической сингонии явля- ется обязательное наличие четырех осей третьего порядка, которые всегда присутствуют в наборе элементов симметрии многогранника.

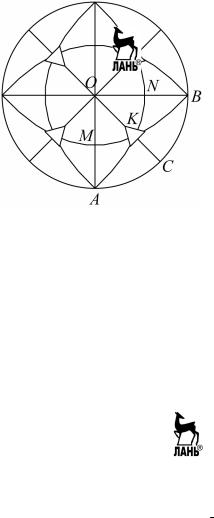
Наличие у кристаллов четырех осей третьего порядка (4L3) позво- ляет быстро и точно строить проекции его осей и плоскостей сим- метрии, в том числе и косо расположенных относительно оси проек- ций. Проводится окружность круга проекций и два взаимно перпен- дикулярных диаметра (рис. 3.5). При этом один из диаметров должен быть направлен на наблюдателя. Под углом 45° к этим диаметрам проводятся еще два диаметра. Затем ножка циркуля ставится на ко- нец одного из первых двух диаметров, а карандаш – на конец пер- пендикулярного диаметра и проводится дуга. Таких дуг нужно про-

37

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

вести четыре. Точки пересечения этих дуг будут проекциями 4L3. Остальные точки пересечения этих дуг, диаметров и окружности - проекции возможных у кристаллов осей симметрия 2-го и 4-го по- рядков. Сами же дуги, окружность и диаметры являются проекциями возможных у кристаллов плоскостей симметрии. Если у кристалла имеются плоскости симметрии, соответствующие каким-то из этих линий, то линии проводятся двойные. Кроме того, эти вспомогатель- ные линии нужны для правильного нанесения проекций граней.

Рис. 3.5. Схема, являющаяся основой для проектирования кубических многогранников

Нужно обратить внимание на то, что плоскости, стереографиче- скими проекциями которых являются линии на рис. 3.5, разбивают поверхность сферы проекций на равные сферические треугольники. Проекции же этих треугольников на круге проекций оказываются неравными. В результате проектирования (лучами зрения) они иска- жаются различно в зависимости от их положения относительно оси проекций. Несмотря на это мы должны видеть, что в результате по- ворота плоскости АСВ вокруг L3, отмеченной буквой K, она совме- щается с плоскостью BNO и с плоскостью ОМА а плоскость ОKС совмещается с плоскостями AKN и ВKМ. В дальнейшем для нас осо- бое значение будет иметь симметричное расположение относительно указанной оси L3 точек А, О и В, дуг KС, KМ и KN, дуг KА, KО и KB, дуг AM, ОN и ВС и дуг МО, NВ и СА.

Оси координат в многогранниках кубической сингонии совмеща- ются или с 3L4, или, в случае их отсутствия, с 3L4 или с 3L2. При

38

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

описании кристаллы кубической сингонии располагаются в про- странстве так, чтобы ось Z была вертикальна. Ось Y располагается слева направо, а ось Х направляется на наблюдателя.

Остальные сведения по методике проектирования кристаллов со- держатся в соответствующем разделе лабораторной работы 2.

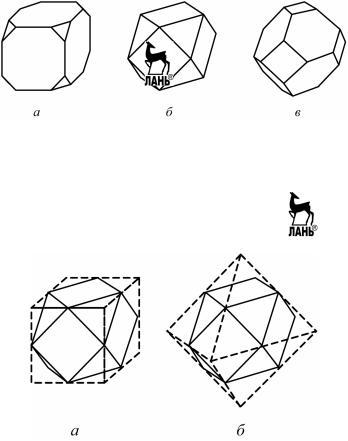
При определении простых форм в кристаллах кубической синго- нии необходимо обращать внимание на число граней данной простой формы, а также мысленно продолжать грани одной простой формы до пересечения их друг с другом (там, где это требуется). Например, на рис. 3.6, а–в представлены многогранники, принадлежащие к классу симметрии m3m, образованные шести- и восьмигранниками.

Рис. 3.6. Три комбинации куба и октаэдра при различном соотношении размеров граней простых форм

В кубической сингонии имеется только один шестигранник – гекса- эдр и один восьмигранник – октаэдр. На рис. 3.7 пунктирными линиями показано, что продолжение квадратных граней до пересечения друг с другом дает гексаэдр, а продолжение треугольных граней дает октаэдр.

Рис. 3.7. Комбинационная форма (сплошная линия) и построение (пунктир), позволяющее видеть простую форму: куб (а); октаэдр (б)

39

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

3.4. Порядок выполнения работы

Для кристаллического многогранника:

1)определить набор элементов симметрии, записать учебный и международный символ точечной группы (класса) симметрии, опре- делить сингонию;

2)выбрать координатные оси и сориентировать многогранник от- носительно круга проекций и наблюдателя;

построить стереографическую проекцию всех элементов сим- метрии;

4)на проекцию элементов симметрии нанести гномостереографи- ческие проекции граней многогранника, обозначая симметрично эк- вивалентные грани (т.е. грани одной простой формы) одинаковыми цифрами;

5)назвать простые формы.

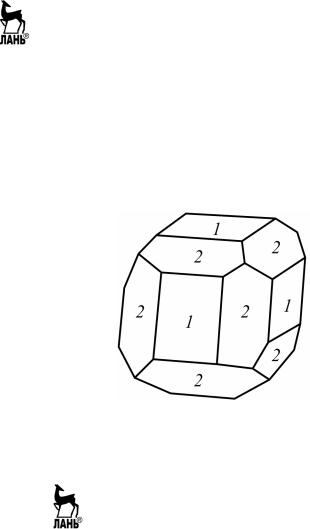
Пример 3.1. Построить стереографическую проекцию элементов симметрии и гномостереографические проекции граней кристалла пирита FeS2, изображенного на рис. 3.8.

Рис. 3.8. Кристалл пирита

1.Кристалл пирита имеет три оси L2, четыре оси L3, три плоскости симметрии Р и центр симметрии С; таким образом, полная совокуп- ность элементов симметрии пирита 4L33L23PC (m3).

2.Выбираем в качестве координатных осей X, Y и Z три взаимно перпендикулярные оси L2.

3.Строим стереографическую проекцию элементов симметрии пирита. Очевидно, что проекция вертикальной оси симметрии второ-

40