
№282. Диденко И. С., Гераськин В. В. Кристаллофизика
.pdf
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
Различают открытые и закрытые простые формы. Закрытые про- стые формы образуют замкнутый объем, открытые – нет.
Рассмотрим простые формы кристаллических многогранников средней и низшей категории (рис. 2.6).
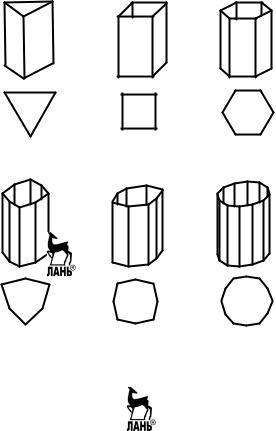
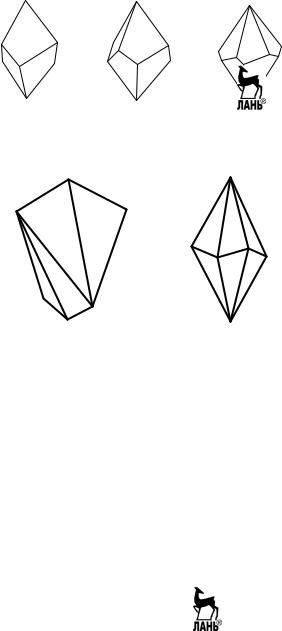
Рис. 2.6. Простые формы кристаллов низшей категории
Моноэдр – одна грань (рис. 2.6, а). Если у кристаллического мно- гогранника имеется неповторяющаяся, единственная, отличающаяся от всех остальных по форме и (или) размеру, грань, то она представ- ляет собой простую форму, называемую «моноэдр». Грань моноэдра не связана с другими гранями элементами симметрии. Пример: грань, лежащая в основании пирамиды.
Пинакоид – две параллельные грани (рис.2.6, б). Диэдр – две непараллельные грани (рис. 2.6, в).
Призма: совокупность граней одинакового размера и формы, пе- ресекающихся по параллельным ребрам (или которые пересекались бы по параллельным ребрам). Призмы в зависимости от формы сече- ния, перпендикулярного ребру, бывают:
–ромбическая (в сечении – ромб) (рис. 2.6, г);
–тригональная (в сечении – равносторонний треугольник) (рис. 2.7, а);
–тетрагональная (в сечении – квадрат) (рис. 2.7, б);
–гексагональная (в сечении – правильный шестиугольник) (рис. 2.7, в). Призмы являются открытыми простыми формами, т.е. граней-
«оснований» у простой формы, называемой призмой, нет. Действи- тельно, призму можно представить себе бесконечную трубу с сечением определенной формы.
21
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
а |
б |
в |
г |
д |
е |
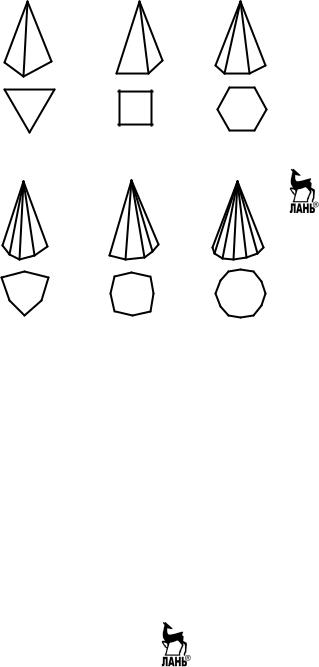
Рис. 2.7. Простые формы кристаллов средней категории: призмы |
||
Пирамида – совокупность |
|
, пересекающихся по ребрам, |
сходящимся в одной точке на |
|
оси симметрии (или которые |
сходились бы в одной точке). |
|
|
Пирамиды, как и призмы, в зависимости от формы сечения, пер- пендикулярного главной оси, бывают ромбическими (рис. 2.6, д), тригональными, тетрагональными и гексагональными (рис. 2.8, а, б, в соответственно).
Так же как и призмы, пирамиды являются открытыми простыми формами, и грань-«основание» пирамиды, как геометрической фигу- ры, не входит в совокупность граней, образующих простую форму «пирамида».
Существуют также дитригональные, дитетрагональные, дигекса- гональные призмы и пирамиды. Приставка «ди» обозначает удвоение числа граней соответствующей простой формы. В этом случае сече- ние пирамиды (или призмы), перпендикулярное ее высоте, представ- ляет собой фигуру, у которой все стороны равны, а соседние углы равны через один (рис. 2.7, г – е и рис. 2.8, г – е).
22
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
а |
б |
в |
г |
д |
е |
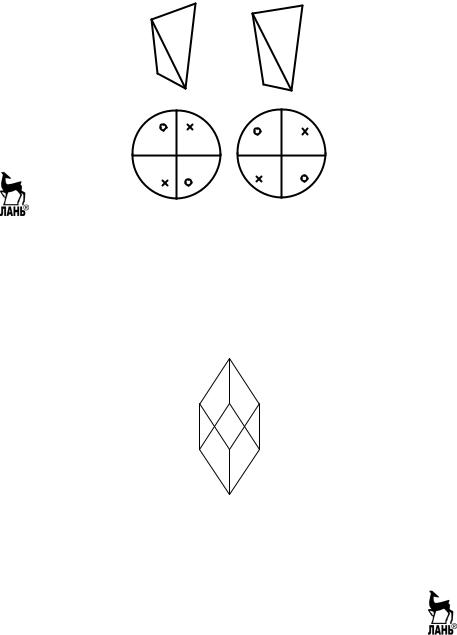
Рис. 2.8. Простые формы средней категории: пирамиды
Дипирамида – фигура, составленная из двух одинаковых пирамид таким образом, что их основания совпадают, например, ромбическая дипирамида (рис. 2.6, е). Дипирамиды представляют собой закрытые простые формы. Отметим существование таких простых форм, как дитригональная дипирамида, дитетрагональная дипирамида, дигек- сагональная дипирамида.
Тетраэдр фигура, имеющая четыре грани, образующие замкну- тый объем. Для не кубических кристаллов различают два вида тетра- эдров: ромбический тетраэдр – соответствует кристаллам низшей категории; центральные сечения, перпендикулярные оси второго по- рядка, представляют собой ромбы; форма грани – косоугольный тре- угольник (все стороны разные) (рис. 2.6, ж); тетрагональный тет- раэдр соответствует кристаллам средней категории; центральное се- чение, перпендикулярное инверсионной оси четвертого порядка представляет собой квадрат; форма – равнобедренный тре- угольник. На рис. 2.9 представлены ромбический и тетрагональный тетраэдры и гномостереографические проекции их граней.
23
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
а |
б |
Рис. 2.9. Ромбический (а) и тетрагональный (б) тетраэдры и гномостереографические проекции их граней
Ромбоэдр – многогранник, который можно получить, если куб вытянуть (или сплюснуть) вдоль одной из осей третьего порядка. При этом грани приобретут форму ромбов (рис. 2.10).
Рис. 2.10. Ромбоэдр
Трапецоэдры – многогранники, грани которых имеют форму тра- пеций. На рис.2.11 представлены тригональный, тетрагональный и гексагональный трапецоэдры.
Скаленоэдры: тетрагональный скаленоэдр можно описать как стую форму, полученную из тетрагонального тетраэдра (рис. 2.12, путем удвоения его граней (каждая грань тетраэдра как бы разломле на на две плоскостью симметрии, нормальной к ней); тригональный скаленоэдр можно аналогично получить из ромбоэдра (рис. 2.12, б).
24
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
а |
б |
в |
|
|
Рис. 2.11. Трапецоэдры: тригональный (а), тетрагональный (б) и гексагональный (в)
а |
б |
Рис. 2.12. Скаленоэдры: тетрагональный (а) и тригональный (б)
2.3. Методика проектирования моделей кристаллических многогранников
До начала проектирования определяется набор элементов симметрии модели кристаллического многогранника. Затем многогранник ориен- тируется (устанавливается) в пространстве. Для этого выбираются кри- сталлографические координатные оси, которые определенным образом располагаются относительно плоскости чертежа и наблюдателя. Поло- жения кристаллографических осей связаны с найденными элементами симметрии: оси координат совпадают либо с осями симметрии, либо с нормалями к плоскостям симметрии, либо с направлениями, параллель- ными ребрам многогранника. Так как при проектировании центр тяже- сти кристалла совмещается с центром сферы проекций, то все элементы симметрии кристалла будут проходить через центр сферы. В эту же точку помещают и начало координат.
Кристаллографическая система координат является правой, т.е. поворот от оси X к Y, от Y к Z и от Z к X происходит против часовой стрелки. Она характеризуется шестью величинами: тремя углами
25
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
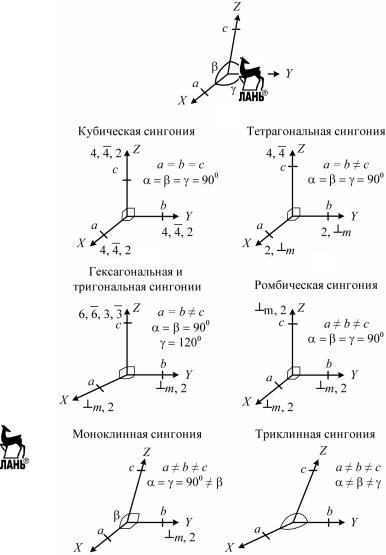
между осями координат (α, β, γ) и единичными параметрами (мас- штабными отрезками) по осям (a, b, c) в соответствии с рис. 2.13, I. Эти шесть величин соответствуют основным трансляциям (парамет- рам) элементарной ячейки кристалла.
I
II |
III |
|
IV |
|
V |
|
|
|
|
|
VII |
VI |
|
|
|
|
|
Рис. 2.13. Кристаллографические системы координат и правила установки кристаллов
26

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
Почти во всех сингониях кристаллографические системы коорди- нат обладают неравными единичными параметрами по осям, а в от- дельных сингониях являются косоугольными. Чтобы это описание было однозначным, существуют правила установки кристаллов, т.е. расположение элементов симметрии, ребер и граней кристаллического многогранника относительно кристаллографических осей XYZ.
Кубическая сингония: a = b = c, α = β = γ = 90°, элементарная ячей- ка – куб. Только здесь кристаллографическая система координат пред- ставляет собой декартову. Оси XYZ параллельны осям симметрии чет- вертого порядка – 3L4, или 3 L4 , если их нет, то 3L2 (рис. 2.13, II).
Тетрагональная сингония: a = b ≠ c, α = β = γ = 90°, элементарная ячейка – призма, в основании которой квадрат. Ось Z параллельна оси высшего L4 или L4 . Оси X и Y лежат в плоскости, пер-
пендикулярной Z, и направлены либо вдоль осей симметрии вто- рого порядка, либо вдоль нормалей к плоскостям симметрии. В от- сутствии этих элементов симметрии оси X и Y ориентируются на грани и ребра кристалла, (т.е. в этом случае необходима дополни- тельная информация) (рис. 2.13, III).
Гексагональная сингония: a = b ≠ c, α = β = 90°, γ = 120°, элемен- тарная ячейка – призма, в основании которой лежит ромб с углом 120° (три такие ячейки составляют шестигранную призму). Ось Z параллельна оси высшего порядка L6, или L6 . Оси X и Y составляют
собой угол 120° и лежат в плоскости, перпендикулярной оси Z. Они направлены либо вдоль нормалей к плоскостям симметрии либо вдоль осей симметрии второго порядка. При наличии обоих элементов симметрии, предпочтение отдается первому варианту, т.е. плоскостям симметрии. В отсутствии этих элементов симметрии оси X и Y ориентируются на грани и ребра кристалла и это дополнитель- но оговаривается (рис. 2.13, IV).
Тригональная сингония: a = b = c, α = β = γ ≠ 90°, элементарная ячей- ка представляет собой ромбоэдр – куб, который вытянули или сплюснули вдоль одной из осей третьего порядка. Оси X, Y и Z выбираются по реб- рам ромбоэдра. Такая система координат называется ромбоэдрической.
Однако для кристаллов тригональной сингонии на практике чаще используют гексагональную установку кристаллографической сис- темы координат. Это возможно, так как элементарный угол поворота оси L3 составляет столько же, что и две операции поворота вокруг оси L6 – 120° (рис. 2.13, IV).
27

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
Ромбическая сингония: a ≠ b ≠ c, α = β = γ = 90°, элементарная ячейка имеет форму «кирпича». Оси X, Y и Z направлены либо вдоль нормалей к плоскостям симметрии, либо вдоль осей симметрии вто- рого порядка (рис. 2.13, V).
Моноклинная сингония: a ≠ b ≠ c, α = γ = 90° ≠ β, элементарная ячейка – параллелепипед, один углов которого не прямой. В кри- сталлах моноклинной сингонии элементами симметрии определяется только одно направление – это ось второго порядка, либо нор- маль к плоскости симметрии. В так называемой стандартной уста- новке вдоль этого направления идет ось Y. Оси X и Z обязательно лежат в плоскости, перпендикулярной оси Y, но их направления не заданы элементами симметрии, и поэтому выбираются вдоль ребер кристалла при условии a < b < c (рис. 2.13, VI).
Триклинная сингония: a ≠ b ≠ c, α ≠ β ≠ γ, элементарная ячейка – параллелепипед, у которого все углы не прямые. Все три оси коор- динат выбираются вдоль ребер кристалла (при условии a < b < c) (рис. 2.13, VII).
При установке кристаллов необходимо также руководствоваться двумя дополнительными положениями:
1)при прочих равных условиях кристалл необходимо устанавли- вать так, чтобы присутствовала единичная грань (см. лабораторную работу 4);
2)удобство проектирования.
Для тригональной и гексагональной сингоний используются не три, а четыре кристаллографические оси. Четвертая горизонтальная ось U нужна того, чтобы грани одной и той же простой формы могли получить одинаковые числовые обозначения (см. лаборатор- ную работу 5).
На рис. 2.14 показаны стереографические проекции кристалло- графических осей координат для кристаллов различных сингоний.
После того как выбраны координатные оси и многогранник со- риентирован, приступают к проектированию в стереографических проекциях найденных элементов симметрии. Проекции распола- гают на круге проекций, который чертится достаточно большим (диаметр 8…10 см). Плоскости симметрии в стереографической проекции изображаются двойными линиями (см. табл. 1.1 лабора- торной работы 1).
28
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
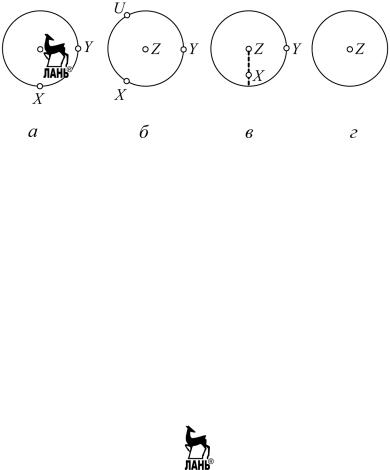
Рис. 2.14. Расположение кристаллографических осей координат на стереографической проекции: для кубической, тетрагональной
и ромбической сингоний (а); для тригональной и гексагональной сингоний (б); для моноклинной сингонии (в); для триклинной сингонии (г)
Стереографическими проекциями осей симметрии являются не кружки и крестики, а соответствующие значки. Выходы горизон- тальных осей, расположенные на окружности круга проекций, со- единяются сплошной линией. Принятые условные обозначения осей симметрии на проекции показаны в табл. 1.2 и 1.3 лабораторной ра- боты 1. В дальнейшем при проектировании граней внутри значков ставятся кружки и крестики (гномостереографические проекции гра- ней). Поэтому не следует рисовать значки слишком мелкими, а также затушевывать их середины.
После того как элементы симметрии многогранника спроектиро- ваны, приступают к проектированию его граней, используя гномо- стереографические проекции. Построение гномостереографических проекций граней кристалла всегда ведется относительно его элемен- тов симметрии, т.е. c учетом взаимного пространственного располо- жения элементов симметрии и нормалей к граням.
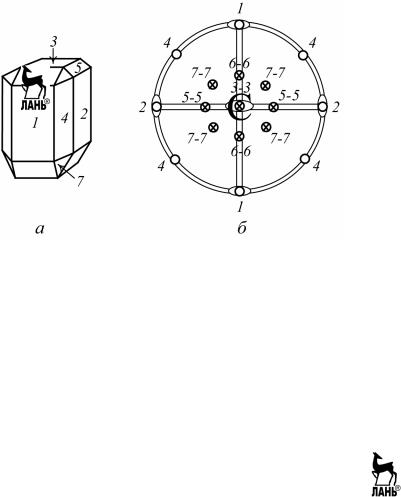
При определении простых форм, входящих в комбинацию, нужно найти число простых форм и назвать простые формы. Число простых форм в комбинации равно числу сортов граней на модели кристалли- ческого многогранника. При подсчете числа простых форм, обра- зующих многогранник, надо отличать это число от числа типов про- стых форм. Например, в кристалле оливина (рис. 2.15, а, б) три типа простых форм – пинакоиды, ромбические призмы и ромбические ди- пирамиды, но семь простых форм – три пинакоида, три ромбические призмы и одна ромбическая дипирамида.
29
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум
Рис. 2.15. Простые формы кристалла оливина: грани 1, 2, 3 – пинакоиды; грани 4, 5, 6 – ромбические призмы; грани 7 – ромбическая дипирамида
2.4.Порядок выполнения работы
1.Определить для кристаллического многогранника набор эле- ментов симметрии. Записать учебный и международный символы точечной группы (класса) симметрии. Определить сингонию.
2.Выбрать координатные оси и сориентировать многогранник от-
носительно круга проекций и наблюдателя (установить кристалл в пространстве).
3.Построить стереографическую проекцию всех элементов сим метрии с верхней полусферы.
4.На проекцию элементов симметрии нанести гномостереографи ческие проекции граней многогранника (с учетом взаимного про- странственного расположения элементов симметрии и нормалей к граням). Обозначить симметрично эквивалентные грани (т.е. грани одной простой формы, одинаковые по форме и величине) одинако- выми цифрами.
5.Назвать простые формы.
Пример 2.1. Построить стереографическую проекцию элементов симметрии и гномостереографическую проекцию граней кристалла серы, изображенного на рисунке 2.16.
30
