Третья минимальная форма.

Доопределим функцию в двух нижних строках таблицы нулём дляи

единицей для 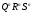. Для этого случая карта Карно показана на рисунке. Её

SnRn	Qn+1
Qn	00	01	11	10
0	0	0	0	1
1	1	0	1	1

единичное покрытие состоит из трёх кубов,

т.е. можно записать: (1.3)

Реализация этого уравнения на элементах И-НЕ может быть получена из следующих преобразований: .

Схема, соответствующая данному уравнению, приведена на рисунке. Уравнения возбуждения внутренних состояний могут быть записаны в виде: ;

Из объединённой карты Карно следует, что при Sⁿ= Rⁿ =1 схема триггера ведёт себя так же, как и в случае, когда

Sⁿ= Rⁿ =0, т.е. сохраняет прежнее состояние. Такой триггер называется Е-триггером, его условное обозначение показано на рисунке:

SnRn		Qn+1
Qn	00	01	11	10
00	11	11	11	11
01	(01)	(01)	(01)	11
11	00	01	00	10
10	(10)	11	(10)	(10)

Временная диаграмма работы Е-триггера приведена на рисунке. Из временной диаграммы следует, что t_n= t_з⁰¹ + t_з¹⁰, т.е. длительность входных сигналов должна быть не менее чем 2t_з^ср; при этом собственная задержка триггера t_зт составляет 4t_з^ср.

Е-триггер может быть реализован на элементах И-ИЛИ-НЕ. Работа этой схемы описывается уравнением :

Уравнения возбуждения имеют вид:

Объединённая карта Карно приведена на рисунке.

SnRn		Qn+1
Qn	00	01	11	10
00	11	01	11	10
01	(01)	(01)	(01)	00
11	00	00	00	00
10	(10)	00	(10)	(10)

Установившиеся значения те же, что и в предыдущем случае, т.е. при Sⁿ= Rⁿ =0 и

Sⁿ= Rⁿ =1 схема сохраняет предыдущее состояние, следовательно это тоже Е-триггер

Четвёртая минимальная форма.

Доопределим функцию Qⁿ⁺¹ в двух нижних строках таблицы: единицей для и нулём для . Тогда получим карту Карно, показанную на рисунке.

SnRn	Qn+1
Qn	00	01	11	10
0	0	0	1	1
1 Рисунок(*)	1	0	0	1

Единичное покрытие этой карты, состоящее из двух кубов, даёт нам следующее уравнение для триггерной схемы:

(1.4)

Реализация этой схемы на элементах И-ИЛИ-НЕ представлена на рисунке. Схема может быть описана посредством следующих уравнений: ;

Составим объединённую карту Карно для полученных уравнений возбуждения.

SnRn		Qn+1
Qn	00	01	11	10
00	11	11	11	11
01	(01)	(01)	00	00
11	00	01	00	00
10	(10)	11	11	(10)

Из анализа карты Карно следует, что такая схема при Sⁿ= Rⁿ =1 не имеет установившихся сочетаний значений и. Кроме того, в схеме возможны состязания сигналов, связанные с тем, что изменение состояния схемы непосредственно влияет на условие прохождения сигнала, вызывающего это изменение. Так, например, появление сигнала Sⁿ=1, когда Qⁿ=0, а =1 вызывает переход в состояние, при котором Qⁿ=0, а =0. При этом нулевое значение запретит дальнейшее действие сигнала Sⁿ.

Для обеспечения устойчивой работы схемы необходимо, чтобы соблюдалось условие =0, но тогда можно записать. ,

т.е. возвращаемся к ранее рассмотренной первой минимальной форме (исключается цепь, показанная на рисунке пунктиром).

Устойчивая работа триггерной схемы, логическое уравнение которой соответствует четвёртой минимальной форме, может быть обеспечена, если во время действия входных сигналов Rⁿ и Sⁿ значения сигналов обратной связи Qⁿ и не будут меняться. Триггерная схема, работа которой характеризуется уравнением (1.4), причём сигналы обратной связи не изменяются во время действия входных сигналов, называетсяJK-триггером. У этого триггера вход J соответствует входу S, а вход K – входу R. Перепишем уравнение (1.4) в новых обозначениях:

(1.5)

Изменение значений сигналов обратной связи в JK-триггере должно происходить после изменения его состояний, т.е. с задержкой на время, не меньшее чем длительность сигналов, вызывавших переход к новому состоянию.

При построении JK-триггеров на потенциальных элементах роль задержки обычно выполняет вспомогательный триггер, который при отсутствии внешних сигналовJиKповторяет (копирует) состояние основного триггера, а в моменты воздействия внешних сигналов сохраняет прежнее состояние. Т.о., потенциальныйJK-триггер представляет собой двухступенчатую триггерную схему, состоящую из двух триггеров – основного или ведущего и вспомогательного или ведомого.

Рассмотрим карту Карно, изображенную на рисунке (*). Эта карта соответствует логическому уравнению JK-триггера с учётом заменыSнаJиRнаK. Из неё следует, что условие переходаJK-триггера из нулевого состояния в единичное может быть выражено в виде:, а условие перехода из единичного состояния в нулевое – в виде.

Поскольку , то вJK-триггере в качестве основной триггерной схемы может быть использованRS-триггер, управляемый по входуRсигналом, а по входуSсигналом, гдеQⁿи- сигналы обратной связи с выходами вспомогательного триггера.

На рисунке приведены логическая структура и условное обозначение асинхронного JK-триггера на потенциальных элементах И-НЕ.

В качестве основного (Т1) и вспомогательного (Т2) триггеров в схеме использованы RS-триггеры на элементах И-НЕ Такая схема носит название триггера с запрещающими связями, поскольку связь между основным и вспомогательным триггером запрещена на время действия единичных значений входных сигналов и. Таблица переходовJK-триггера приведена на рисунке. Из таблицы следует, что основное отличие JK-триггера от

Sn	Rn	Qn+1
0 0 1 1	0 1 0 1	Qn 0 1

RS-триггера состоит в том, что одновременное поступление сигналов

на входы J и K приводит к изменению состояния триггера на противоположное. Таким образом, объединение входов превращает JK-триггер в триггер с одним входом (Т-триггер). На схеме вход Т показан пунктиром .

Временная диаграмма работы JK-триггера используемого в качестве Т-триггера, приведена на рисунке:

Из временной диаграммы следует, что длительность сигналов на входе Т должна удовлетворять условию t_с >= 2t_з^ср.

Задержка переключения основного триггера равна t_зт1=3t_з^ср, а задержка переключения вспомогательного триггера равнаt_зт2=4t_з^ср. Полная задержка переключения триггерной схемыt_зттзависит от длительности сигнала на входе Т и равна:t_зтт =t_с+t_зт2.

Состязания сигналов в логических схемах.

_____Реализация любой логической схемы всегда исходит из ее логического уравнения. На самом деле, логическое уравнение представляет собой идеализированное описание схемы. Идеализация связана с тем, что при логическом описании схем задержки в них не учитываются. Наличие задержек в логических схемах приводит к тому, что в некоторые моменты времени не подтверждаются основные аксиомы алгебры логики

и.

_____Рассмотрим реализацию уравненияна элементах И-НЕ и реализацию уравненияна элементах ИЛИ-НЕ с некоторой фиксированной задержкойt_з^ср.

Из временной диаграммы работы этих двух схем следует, что на их выходе имеется ложный сигнал, длительность которого определяется величиной задержки в элементе инверсии. Подобная ситуация может возникнуть всегда, когда при изменении входных сигналов выходной сигнал остается постоянным (статический риск сбоя). Ситуации, при которых может появиться риск сбоя, носят название состязаний или гонок.

В последовательностных схемах (автоматах), т.е. в схемах, имеющих цепи обратной связи, состязания могут возникать либо между внешними сигналами и сигналами обратной связи, либо только между сигналами обратной связи, изменяемыми под действием внешних сигналов. Такие состязания называются существенными или критическими. Состязания в последовательностных схемах проверяются путем анализа таблицы переходов и уравнений возбуждения.

При этом анализ проводится при следующих предположениях:

1. В каждый момент времени может происходить изменение только одного внешнего сигнала (между внешними сигналами состязаний нет); 2. При переходе от одного устойчивого состояния к другому меняется не более одного выходного сигнала; 3. Если при изменении внешнего входного сигнала состояние схемы меняется, то оно будет изменяться либо как сам внешний сигнал, либо как его инверсия.

Схемы триггеров являются простейшими цифровыми автоматами и относятся к классу последовательностных схем. Поэтому в них возможны состязания сигналов. Схемы триггеров, реализующие первую, вторую и третью минимальные формы, не имеют состязаний, поскольку при любых переходах из одного устойчивого состояния в другое входы не принимают значения вида или.

Анализ схемы триггера, соответствующего четвертой минимальной форме, приведенной в предыдущей лекции, свидетельствует о наличие состязаний. Пусть в исходном состоянии Sⁿ = Rⁿ = 0 ; тогда при измененииRⁿс 0 на 1Qⁿ⁺¹либо будет оставаться постоянным и равным 0, либо будет меняться с 1 на 0, т.е. как. Таким образом, в данном случае состязаний нет. ЕслиRⁿбудет оставаться постоянным, аSⁿменяться с 0 на 1, тобудет либо постоянно, либо меняться с 1 на 0, т.е. в этом случае в элементе возникают состязания.

Возможность появления состязаний, как в комбинационных схемах, так и на входах запоминающих элементов, требует, чтобы были приняты специальные меры для исключения сбоев в аппаратуре. Основным средством, позволяющим исключить влияние состязаний служит введение стробирования. Под стробированием понимается выделение из информационного сигнала той части, которая свободна от ложных сигналов, вызванных гонками.

Всякая комбинационная логическая цепь заканчивается запоминающим элементом, т.е. триггером. Поэтому при построении устройств на потенциальных элементах стробирование вводят на входах триггерных схем.

Синхронные триггеры.

Триггерные схемы, входные сигналы которых стробируются специальными периодическими импульсными сигналами носят название синхронных триггеров.

Процесс стробирования периодическими сигналами называется синхронизацией, а время, равное периоду следования синхросигналов T_cc - тактом. Наряду с защитой от состязаний, введение синхронизации позволяет создать условия для одновременного изменения состояний многих триггерных схем (синхронная работа). Состояние синхронных триггеров обозначаютQⁿ⁺¹. Под индексом n+1 подразумевают период времени, следующий за периодом (тактом) n, в течении которого могло произойти изменение состояния триггера.

Приведем примеры схем синхронных триггеров, построенных на основе рассмотренных ранее асинхронных триггеров. Для построения таких триггеров сигналы Rⁿ иSⁿв уравнении, описывающем работу асинхронного триггера, необходимо заменить на сочетания сигналовCⁿRⁿ иCⁿSⁿсоответственно, гдеCⁿ- сигнал стробирования или синхронизации в момент времени n.

Перепишем уравнение триггера, соответствующего первой минимальной форме, в виде:

Преобразуем это выражение к виду, удобному для реализации триггера на элементах И-НЕ:

Логическая структура и условное обозначение синхронного RS-триггера:

Из временной диаграммы работы этого триггера следует, что время переключения триггера равно:

Для надежной работы схемы необходимо, чтобы длительность переключающего сигнала была больше времени переключения, т.е. длительность синхросигнала t_ccдолжна удовлетворять условиюt_cc>>2t_з^ср.. Общая задержка в рассмотренной схеме составляет:

Для построения схемы синхронного RS-триггера, соответствующей первой минимальной форме, на элементах И-ИЛИ-НЕ выполним преобразования:

Логическая схема и условное обозначение триггера, реализующая последнее уравнение:

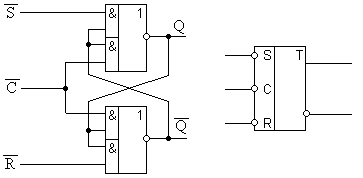
Из временной диаграммы видно, что задержка в таком триггере составляет

.

На входы триггера подаются инверсные значения сигналов. Аналогичным образом могут быть построены синхронные триггеры, соответствующие второй минимальной форме:

Схема триггера, соответствующая данному уравнению, условное обозначение и временная диаграмма его работы:

Поскольку на входы схемы поступают инверсные значения входных сигналов, ее условное обозначение совпадает с условным обозначением предыдущей схемы. Отличие схемы состоит в том, что ее задержка больше задержки предыдущего триггера и составляет:

Более быстродействующая схема может быть построена при реализации уравнения, соответствующего второй минимальной форме, на элементах И-ИЛИ-НЕ. Для этого исходное уравнение следует привести к виду:

Логическая структура, условное обозначение и временная диаграмма работы такого триггера:

Время переключения и задержка триггера равны:

_____Все описанные триггеры относятся к категории синхронных RS-триггеров. Правильная работа таких триггеров обеспечивается при соблюдении условия: CRS=0.

Схемы синхронных триггеров могут иметь несколько синхронных и асинхронных входов R и S. При этом сами входы R и S могут быть соединены конъюнктивно или дизъюнктивно.

_____Наличие стробирования по времени на информационных входах триггера позволяет разделять время его работы на два чередующихся интервала. Первый интервал равен длительности сигнала синхронизации. В течении этого интервала времени может происходить изменение состояния триггера, а следовательно и значений выходных сигналов.

В течение следующего интервала времени состояние триггера и значение его выходных сигналов остаются постоянными. Таким образом, информация заносится в триггер в течение первого интервала, а в течение последующего интервала времени она может быть использована. Это свойство синхронных триггеров в течение определенного промежутка времени сохранять неизменным значение выходных сигналов позволяет строить на их основе триггеры задержки - D-триггеры.

_____Важнейшее свойство D-триггеров в том, что, как только на вход С поступает импульс на выходе Q устанавливается тот же уровень напряжения, который этот момент действует на входе D, т.е. переброс триггера происходит с некоторым отставанием dt относительно смены сигнала на входе D.

Логическое уравнение синхронного D-триггера может быть получено из логического уравнения синхронного RS-триггера путем замены сигнала SнаD, а.

_____Таким образом, синхронные RS-триггеры, схемы которых рассмотрены ранее, могут непосредственно использоваться в качестве-триггеров. Поскольку работа этих триггеров обеспечивается при наличии как сигнала, так и его инверсии, такие триггеры носят название синхронных-триггеров с парафазными входами.

D-триггеры, управляемые только прямым значением сигнала D, могут быть построены как на элементах И-НЕ, так и ИЛИ-НЕ. Преобразуем логическое уравнение, описывающее работу синхронного триггера на элементах И-НЕ путем замены SнаD, ак виду:

(*)

Схема, реализующая это уравнение и ее условное обозначение показаны на рисунке:

Особенность синхронных D-триггеров состоит в том, что изменение информации на входе D во время действия синхросигналов непосредственно отражается на изменении значения выходных сигналов и. В интервале времени между синхросигналами триггер будет сохранять ту информацию, которая присутствовала на входе D в момент окончания действия синхросигнала.

Сигналы информации на ходе D должны охватывать задний фронт (срез) сигналов синхронизации. При этом время перекрытия сигналов C и D должно быть не меньше, чем время переключения триггера.

Логическое уравнение для RS-триггера, используемого в режиме D-триггера, может быть представлено виде:

Полученное уравнение легко реализуется схемой на элементах И-ИЛИ:

После известных преобразований:

или

уравнению будут соответствовать схемы, построенные на элементах И-НЕ; ИЛИ-НЕ:

Для управления этими схемами требуются синхросигналы обеих полярностей, кроме того, эти схемы не имеют инверсного выхода.

Одноступенчатый D-триггер, управляемый двумя полярностями синхросигналов, носит название триггера - "защелки". Все приведенные схемы триггера - "защелки" налагают весьма жесткие требования на фазировку сигналов синхронизации. Для устойчивой работы схем необходимо, чтобы срез сигнала D отставал от фронта сигнала . Если сигналзадержан относительно сигналана время, большее, чем время переключения триггера, то схема может работать неправильно.

Одной из разновидностей D-триггера является DV-триггер, который отличается от D-триггера наличием дополнительного управляющего входа V. Сигнал на этом входе либо разрешает, либо блокирует действие сигнала С. Поэтому, чтобы получить логическое уравнение для DV-триггера, необходимо логическом уравнении D-триггера заменить переменную С логическим произведением CV.

Так, из (*)путем замены С на CV получаем уравнение для DV-триггера на элементах И-НЕ:

Соответствующая схема триггера:

здесь же приведено условное обозначение DV-триггера.

К длительности сигнала V предъявляются те же требования, что и к длительности сигнала D.

В рассмотренных синхронных триггерах типов RS, D, DV состояние триггера в такте n+1 определялось либо значением внешних сигналов, либо сигналов обратной связи в такте n. В ранее рассмотренных триггерах типов JK и T состояние триггера в такте n+1 зависит от соотношения значений внешних сигналов и сигналов обратной связи в такте n. Поскольку значение выходного сигнала является однозначным только в паузе между синхросигналами, то для построения JK- и T-триггеров необходимо, чтобы изменение выходных сигналов осуществлялось с задержкой, равной длительности синхросигнала. Аналогичная задача возникает, когда необходимо передавать информацию с выхода одного триггера на вход последующего с помощью одного и того же синхросигнала, например при построении регистровых и пересчетных схем.

В синхронной триггерной схеме необходимая задержка может быть образована с помощью дополнительного D-триггера, на синхронизирующий вход которого подано инверсное значение синхросигнала. Таким образом, синхронный триггер с задержкой является триггерной схемой с двухступенчатым запоминанием информации. Первая ступень (ведущий триггер) воспринимает сигнал в течение времени, равного длительности синхросигнала, и реализует логическое уравнение триггера, а вторая ступень (ведомый триггер) хранит предыдущее состояние, пока не окончится действие синхросигнала. На рисунке приведены логическая структура и условное обозначение RS-триггера с двухступенчатым запоминанием информации:

Правильная работа пары "ведущий-ведомый" в данной схеме обеспечивается, если задержка в элементе инверсии не превышает задержки основного триггера.

При построении триггера с двухступенчатым запоминанием информации для ведущего и ведомого триггеров могут применяться различные схемы синхронных триггеров. На рисунке приведена логическая структура двухступенчатого RS-триггера, у которого в качестве ведущего триггера применен триггер с прямым управлением, а в качестве ведомого - триггер с инверсным управлением:

Как и в предыдущей, в данной схеме синхросигналом для ведомого триггера служит пауза между синхросигналами ведущего триггера.

Для построения синхронных JK- и Т-триггеров использовалась двухступенчатая триггерная схема с запрещающими связями (см. пред. лекцию). Эта же схема может быть использована и в качестве синхронного триггера, если на ее входах сигналы J и К заменить логическими произведениями JC и КС соответственно, где С - сигнал синхронизации. Подобным же образом строятся схемы JK- и Т-триггеров на двухступенчатых RS-триггерах.

_____На рисунке приведена логическая структура синхронного JK-триггера (вход Т показан пунктиром), построенного на RS-триггерах.

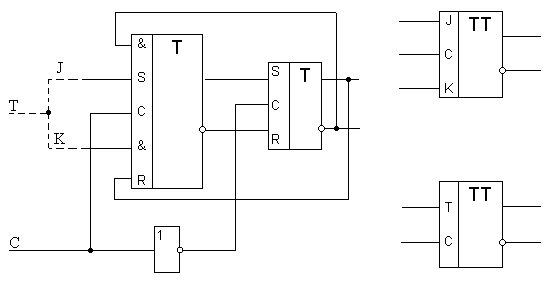
На этом же рисунке приведены условные обозначения синхронных JK- и Т-триггеров. Для устойчивой работы двухступенчатого триггера длительность синхросигналов t_ccдолжна быть больше времени переключения триггераt_{n T1}, используемого в качестве ведущего, а пауза между синхросигналами больше, чем время переключенияt_{n T2}ведомого триггера. Задержка информационного сигнала в двухступенчатой триггерной схеме (t_{з ТТ}) зависит от длительности синхросигнала и равна:

где t_{n T2}-задержка ведомого триггера.

Схема преобразования JK-триггера в D-триггер.

Две схемы преобразования JK-триггера в T-триггер.

D-триггер, если того требуют обстоятельства, можно использовать как RS-, JK- или как Т-триггер. Это легко осуществить с помощью дополнительных связей между входами и выходами или добавлением логических элементов.

D-триггер ТТЛ в роли RS-триггера с инверсными входами (асинхронный).

D-триггер ТТЛ в роли синхронного RS-триггера с инверсными входами.

D-триггер в роли синхронного JK-триггера.

Схема преобразования D-триггера в Т-триггер.

JK-триггер в роли синхронного RS-триггера