Мелишева Е.П.
Правила выполнения и оформления контрольных работ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради чернилами любого цвета, кроме красного. Необходимо оставлять поля для замечаний рецензента.
2. В заголовке работы на обложке должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, номер контрольной работы.
3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задания, а также задачи не своего варианта, не засчитываются.
4. Решения задач надо располагать в порядке возрастания их номеров, указанных в задании, сохраняя номера задач.
5. Перед решением каждой задачи надо полностью выписать ее условие.
6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7. После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить работу над ошибками в той же тетради.
Вариант 1
I. Найти пределы функций, не пользуясь правилом Лопиталя:
а)
б)
в)
г)
.
II.
Найти производные
данных функций.
а)
б)
в)
III.
Найти:
и
для функции
IV.
Исследовать методами дифференциального
исчисления функцию
и, используя результаты исследования,
построить ее график:
.
V. Найти неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
а) 
б)
в) 
г)
.
VI.
Сделать чертеж и вычислить площадь
фигуры, ограниченной линиями:
и
.
VII. Найти общее или частное решение данного дифференциального уравнения.
а)
,
б)
,
в)
,
,
VIII. Исследовать сходимость рядов:
а)
,
б)
,
в)
,
г)
,
д)
.
IX. Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости
.
X.
Дана функция
,
точка
.
Требуется:
а) Найти частные производные I и II порядка;
б)
Составить уравнения касательной
плоскости и нормали в точке
;
в) Исследовать на экстремум.
, 
.
XI.
Полученные из опыта значения функции
при различных значениях независимой
переменной приведены в таблице. Методом
наименьших квадратов найти функцию
в виде
.
Сделать чертеж.
-
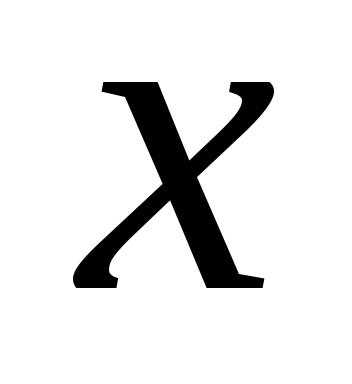
-2,1
-1,3
0,1
0,9
1,5
2,1
3,4
3,9
4,2
5,3
28,6
23,1
13,3
7,7
3,5
-0,6
-9,8
-13,2
-15,5
-23,2
Вариант 2
I. Найти пределы функций, не пользуясь правилом Лопиталя:
а)
б)
в)
г)
.
II.
Найти производные
данных функций.
а)
б)
в)
III.
Найти:
и
для функции
IV.
Исследовать методами дифференциального
исчисления функцию
и, используя результаты исследования,
построить ее график:
.
V. Найти неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
а) 
б)
в) 
г)
.
VI.
Сделать чертеж и вычислить площадь
фигуры, ограниченной линиями:
и
.
VII.Найти общее или частное решение данного дифференциального уравнения.
а)
,
б)
,
в)
,
,
.
VIII.Исследовать сходимость рядов:
а)
,
б)
,
в)
,
г)
.
д)
.
IX. Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости
.
X.
Дана
функция
,
точка
.
Требуется:
а) Найти частные производные I и II порядка;
б)
Составить уравнения касательной
плоскости и нормали в точке
;
в) Исследовать на экстремум.
, 
.
XI.
Полученные из опыта значения функции
при различных значениях независимой
переменной приведены в таблице. Методом
наименьших квадратов найти функцию
в виде
.
Сделать чертеж.
-
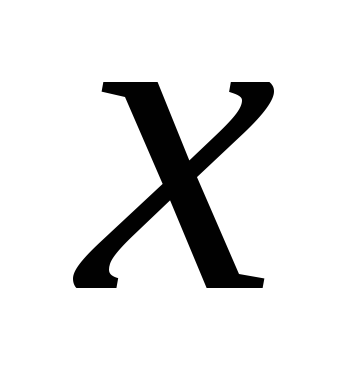
7,4
8,2
9,6
10,3
12,8
14,9
15,3
16,9
18,1
19,5
20,3
-7,7
-6,7
-5,3
-4,6
-2,1
-0,1
0,2
1,8
3,0
4,4
5,2