5.4 Степенные ряды

ОПРЕДЕЛЕНИЕ. Функциональным рядом называют выражение

,

члены которого являются функциями отx, определенными на некотором множестве X.

Если задать переменной числовое значение, то получится числовой ряд,

который может быть как сходящимся, так и расходящимся.

ОПРЕДЕЛЕНИЕ. Множество значений , при которых функциональный ряд сходится, называется его областью сходимости.

В области сходимости сумма функционального ряда является некоторой функцией от переменной и определяется как

.

Например, ряд

сходится, если (члены ряда образуют геометрическую прогрессию со знаменателем), и расходится, если.

Областью сходимости ряда служат два промежутка и.

Одним из видов функциональных рядов являются степенные ряды, которые записывают:

,

где - последовательность действительных чисел, коэффициенты ряда;- центр области сходимости ряда.

Если степенной ряд принимает вид:

.

Рассмотрим свойства степенных рядов на примере ряда (*), т.к. любой степенной ряд общего вида легко преобразовать к виду (*) подстановкой .

Теорема Абеля

Если степенной ряд сходится в точке, то он сходится абсолютно в интервале, т.е. при всехx, удовлетворяющих условию .

ДОКАЗАТЕЛЬСТВО

По условию теоремы в точке степенной ряд сходится. Общий член сходящегося числового ряда , в силу необходимого признака, стремится к нулю:, поэтому все члены ряда ограничены некоторым числом:. То есть

.

Представим степенной ряд в виде

и составим ряд из абсолютных величин его членов:

.

Сравним его с рядом, составленным из членов геометрической прогрессии: . Этот ряд сходится, еслии знаменатель прогрессии

В силу неравенств , члены рядаменьше соответствующих членов сходящегося ряда, по первому признаку сравнения, рядтакже сходится.

Мы показали, что при любом из интерваластепенной рядсходится, значит, рядвнутри этого интервала сходится абсолютно.

Следствие. Если степенной ряд расходится в точке, то он расходится при любомx, по модулю, большем, чем b, т.е. если

Таким образом, можно сказать, что для любого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число R, что для всех x, по модулю меньших R (), ряд сходится абсолютно, а для всех x, по модулю больших R (), ряд расходится.

ОПРЕДЕЛЕНИЕ. Радиусом сходимости степенного ряда называют такое числоR, что для всех ,, степенной ряд сходится, а для всех,, расходится. Интервалназывают интервалом сходимости степенного ряда.

Замечание. Для степенного ряда областью сходимости служит интервалсимметричный относительно точки_.

На границах интервала сходимости, в точках степенной рядможет вести себя различным образом.

ПРИМЕР. Найти интервал и область сходимости степенного ряда

.

РЕШЕНИЕ

Рассмотрим ряд, составленный из абсолютных величин .

Все члены этого ряда положительны, поэтому к нему можно применить признак Даламбера: ,

.

Найдем значения , при которых этот предел будет меньше единицы, т.е. решим неравенство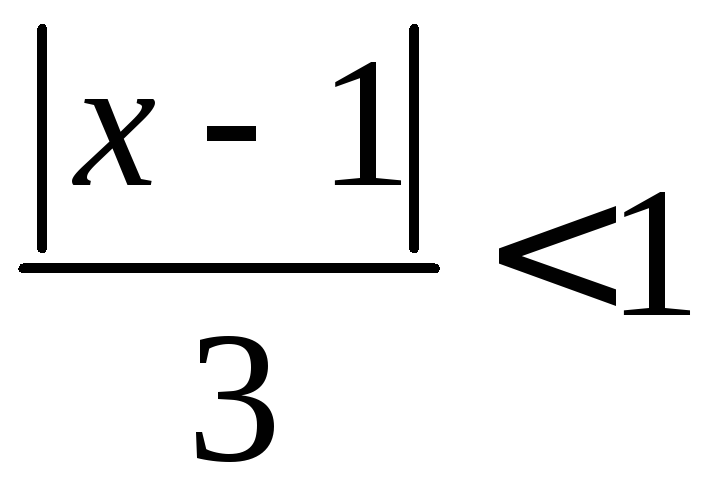. Умножим обе части неравенства на 3:и запишем полученное неравенство в виде двойного неравенства:. Интервал симметричен относительно точки, а радиус сходимости

Исследуем сходимость ряда на концах интервала. В точке получим ряд с положительными членами

.

Это обобщенный гармонический ряд, который, как мы знаем, расходится ().

В точке получим знакочередующийся ряд

.

Его сходимость обсуждалась выше, было доказано что ряд сходится условно.

Окончательно, областью сходимости степенного ряда является промежуток , причем, еслиряд сходится условно. Радиус сходимости степенного ряда равен

ПРИМЕР. Найти интервал сходимости ряда .

РЕШЕНИЕ

Общий член ряда имеет вид , тогда.

Составим ряд из абсолютных величин и применим к нему признак Даламбера: .

После сокращения на множители ии вынесения за знак предела множителя, не зависящего отn, выражение примет вид:

.

Таким образом, предел равен нулю при любом x, т.е. по признаку Даламбера областью сходимости этого ряда является вся числовая ось.