
- •Федеральное агентство по образованию
- •М. М. Афанасьева, о.С. Громова, в. А. Павский
- •В 3-х частях
- •Часть 2
- •Isb n 5-89289-216-6
- •Правила выполнения и оформления контрольных работ
- •Тема 1. Функции нескольких переменных
- •1.1 Общие сведения
- •1.2 Производные и дифференциалы
- •1.3 Экстремумы функции нескольких переменных
- •1.4 Скалярное поле. Производная по направлению. Градиент
- •Тема 2. Комплексные числа
- •Комплексная плоскость
- •Действия над комплексными числами
- •Тема 3. ОпределенныЙ и неопределенный интегралы
- •3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла
- •Определенный интеграл
- •I этап.
- •Связь интегрирования с дифференцированием
- •Неопределенный интеграл
- •Формула ньютона-лейбница
- •, Где .
- •Свойства интегралов
- •Метод интегрирования по частям
- •3.3 Основные классы интегрируемых функций
- •Интегрирование рациональных функций
- •1 Случай.
- •2 Случай.
- •3 Случай.
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •3.4 Несобственные интегралы
- •Несобственный интеграл с бесконечными пределами
- •Несобственный интеграл от неограниченной функции
- •3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей
- •Вычисление длины дуги плоской кривой
- •Вычисление объёмов
- •Тема 4. Дифференциальные уравнения
- •4.1 Основные понятия
- •4.2 Дифференциальные уравнения 1-го порядка
- •Дифференциальные уравнения с разделёнными переменными
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •4.3 Дифференциальные уравнения второго порядка
- •Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные уравнения 2-го порядка с постоянными коэффициентами
- •4.4 Задачи на составление дифференциальных уравнений
- •Тема 5. Ряды
- •5.1 Числовые ряды
- •5.2 Числовые ряды с положительными членами
- •Интегральный признак Коши
- •Первый признак сравнения
- •Второй признак сравнения
- •Признак Даламбера
- •5.3 Знакопеременные ряды
- •Знакопеременные ряды. Абсолютная и условная сходимость
- •Достаточный признак сходимости
- •5.4 Степенные ряды
- •Теорема Абеля
- •Свойства степенных рядов
- •5.5 Разложение функции в степенной ряд. Ряд Тейлора
- •Разложение по степеням X некоторых элементарных функций
- •5.6 Применение степенных рядов Интегрирование функций
- •Интегрирование дифференциальных уравнений
- •Контрольные задания
- •9. . 10..
Вычисление длины дуги плоской кривой
Пусть
имеется дуга
![]() некоторой кривой, впишем в неё ломаную
линию, и будем увеличивать число звеньев
ломаной таким образом, чтобы наибольшая
из длин отрезков стремилась к нулю (рис.
21). Если при этом периметр ломаной будет
стремиться к определенному пределу, не
зависящему от того, какие ломаные мы
вписываем, то дуга называетсяспрямляемой,
а предел - длиной
этой
дуги.
некоторой кривой, впишем в неё ломаную
линию, и будем увеличивать число звеньев
ломаной таким образом, чтобы наибольшая
из длин отрезков стремилась к нулю (рис.
21). Если при этом периметр ломаной будет
стремиться к определенному пределу, не
зависящему от того, какие ломаные мы
вписываем, то дуга называетсяспрямляемой,
а предел - длиной
этой
дуги.
Р ассмотрим
задачу о вычислении длины дуги
ассмотрим
задачу о вычислении длины дуги![]() кривой
кривой![]() ,
заданной в декартовой системе координат,
если
,
заданной в декартовой системе координат,
если![]() - дифференцируемая функция, имеющая
непрерывную производную в промежутке
- дифференцируемая функция, имеющая
непрерывную производную в промежутке![]() ,
причем точкам
,
причем точкам![]() и
и![]() соответствуют значения
соответствуют значения![]() и
и![]() .
.
Пусть
![]() - вписанная ломаная. Её вершинам
соответствуют значения
- вписанная ломаная. Её вершинам
соответствуют значения![]() и
и![]() .
Произвольно выберем отрезок
.
Произвольно выберем отрезок![]() и вычислим его длину (рис. 22):
и вычислим его длину (рис. 22):
![]() ,
где
,
где
![]() ,
,![]() ,
,![]() .
.
По теореме Лагранжа о конечных приращениях
![]() .
.
Подставим
![]() и получим
и получим
![]() .
.
Д ля
периметра всей ломаной получим формулу:
ля
периметра всей ломаной получим формулу:
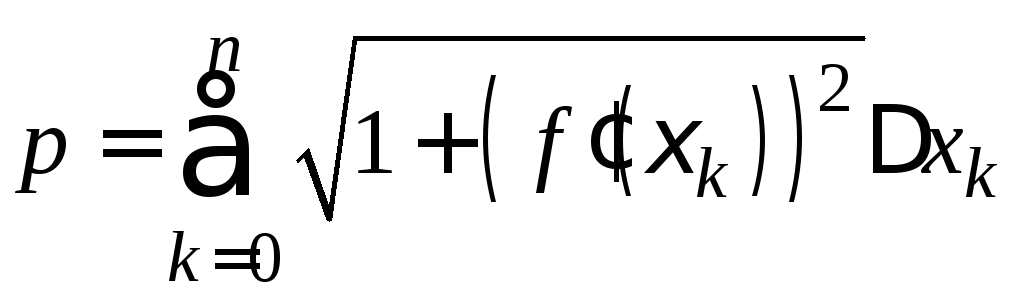 ,
,
и так как длина дуги по определению равна пределу данной интегральной суммы, можем записать
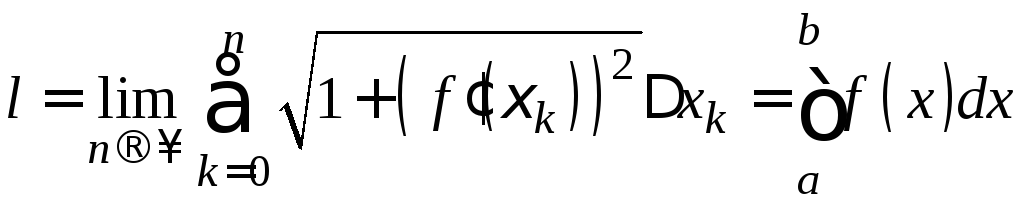 .
.
При
параметрическом способе задания кривой
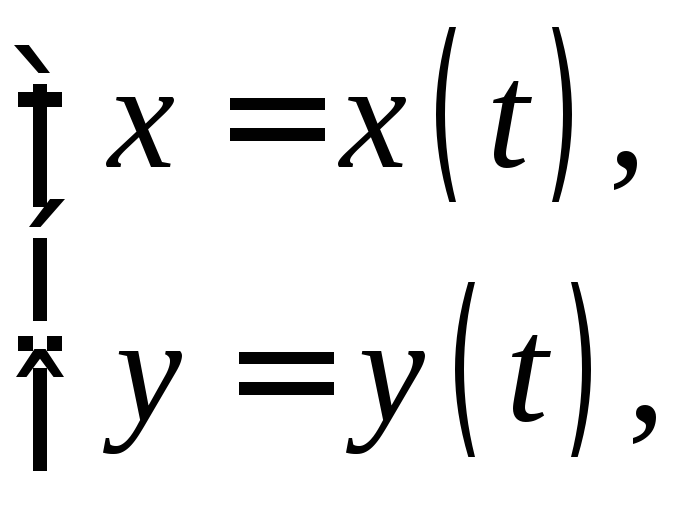
так
как ![]() ,
а
,
а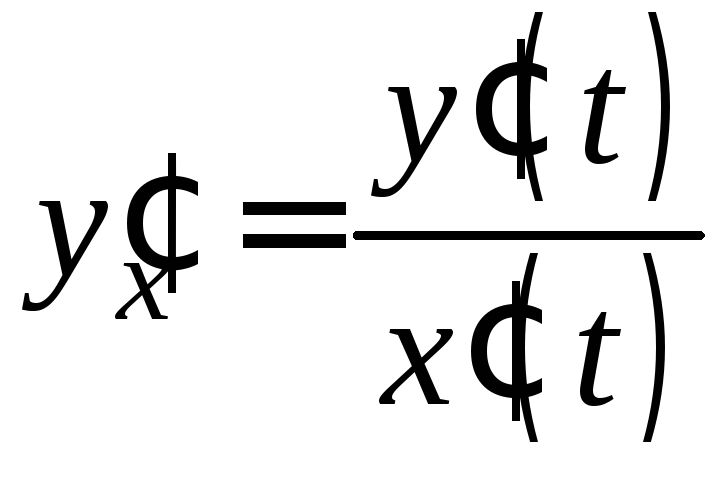 ,
имеем
,
имеем
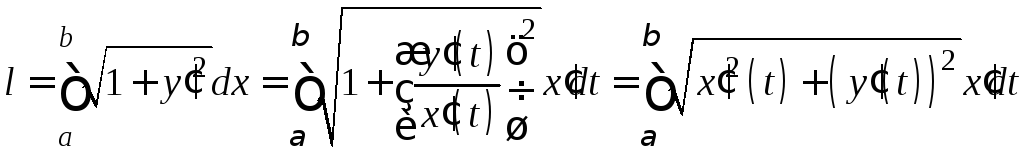 ,
,
где
![]() и
и![]() - значения параметра на концах дуги,
причём
- значения параметра на концах дуги,
причём![]() ,
,![]() .
.
В
случае если кривая задана в полярных
координатах
![]() ,
длина дуги
,
длина дуги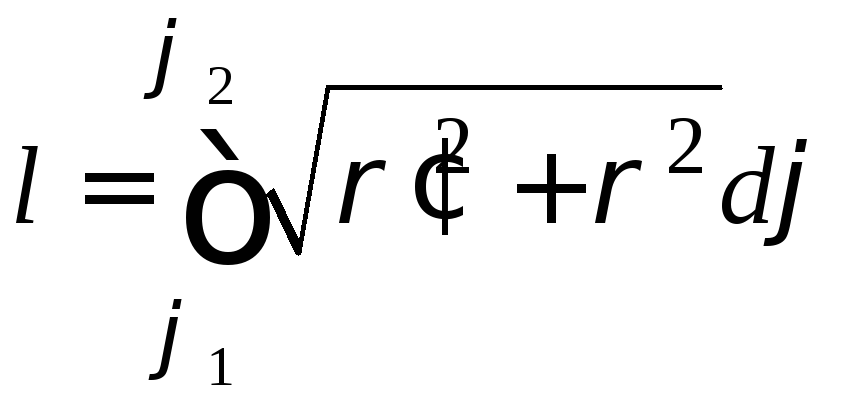 ,
,
где
![]() и
и![]() - значения аргумента
- значения аргумента![]() на концах дуги кривой.
на концах дуги кривой.
ПРИМЕР. Найти
длину дуги кривой
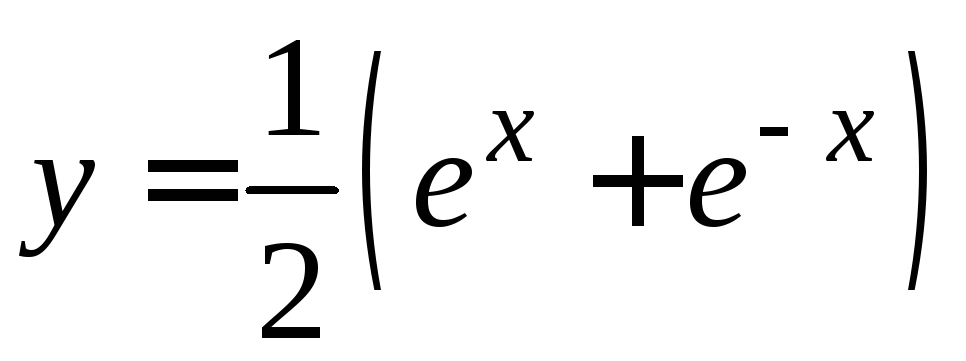 ,если
,если
![]() изменяется от 0 до 1.
изменяется от 0 до 1.
РЕШЕНИЕ
Воспользуемся
формулой
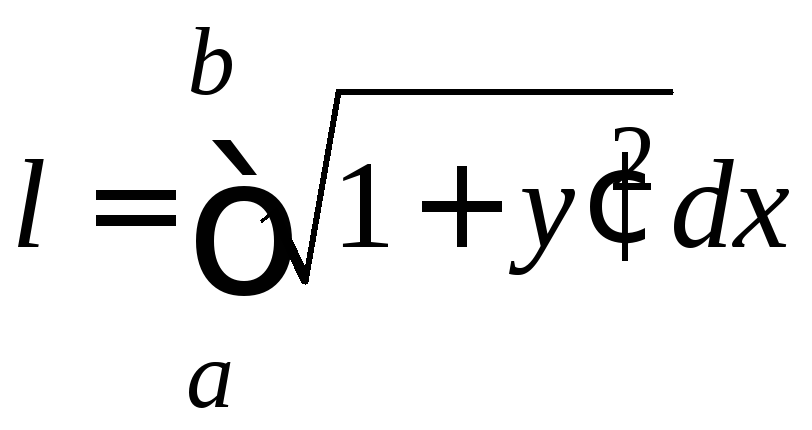 .
Найдём
.
Найдём![]() :
: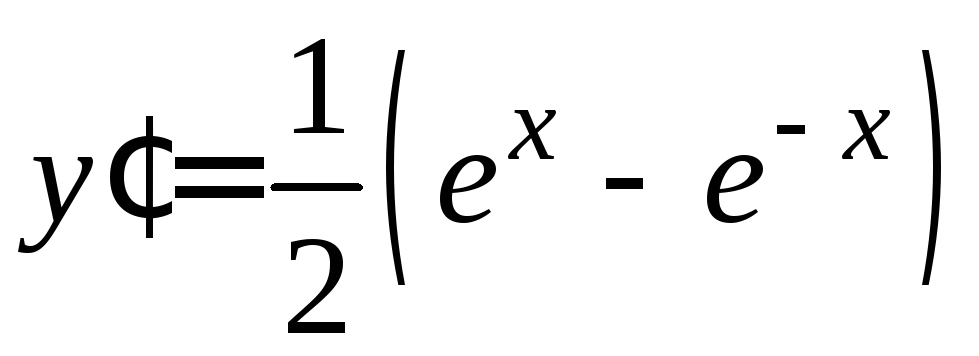 .
Подставим полученную производную в
формулу длины дуги, тогда
.
Подставим полученную производную в
формулу длины дуги, тогда
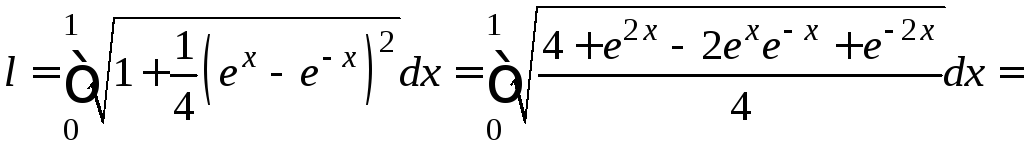
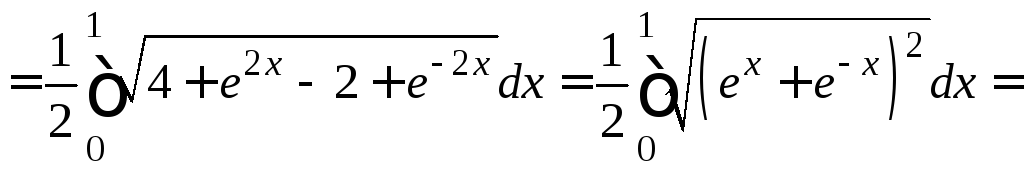
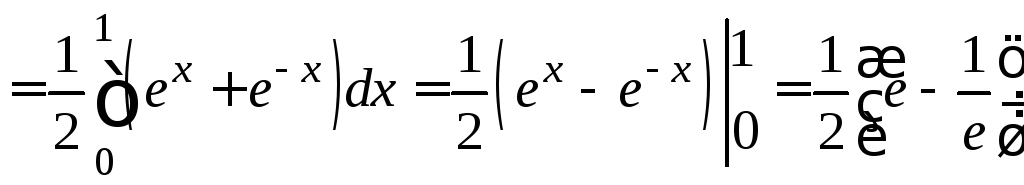 .
.
Вычисление объёмов
Рассмотрим
тело, ограниченное замкнутой поверхностью.
Пересечём его плоскостью, перпендикулярной
к любой из его осей, например к оси
![]() .
Будем считать, что площадь сечения
является заданной функцией
.
Будем считать, что площадь сечения
является заданной функцией![]() его расстояния от начала координат.
Предположим, что тело заключено между
двумя плоскостями
его расстояния от начала координат.
Предположим, что тело заключено между
двумя плоскостями![]() и
и![]() .
Объём такого тела вычисляется по формуле
.
Объём такого тела вычисляется по формуле
 .
.
Е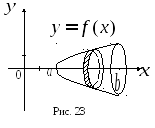 сли
тело, объём которого предстоит вычислить,
получено в результате вращения непрерывной
кривой с уравнением
сли
тело, объём которого предстоит вычислить,
получено в результате вращения непрерывной
кривой с уравнением![]() вокруг оси
вокруг оси![]() ,
то в сечении получается круг радиуса
,
то в сечении получается круг радиуса![]() (рис. 23). Следовательно, площадь поперечного
сечения
(рис. 23). Следовательно, площадь поперечного
сечения![]() ,
,
а объём
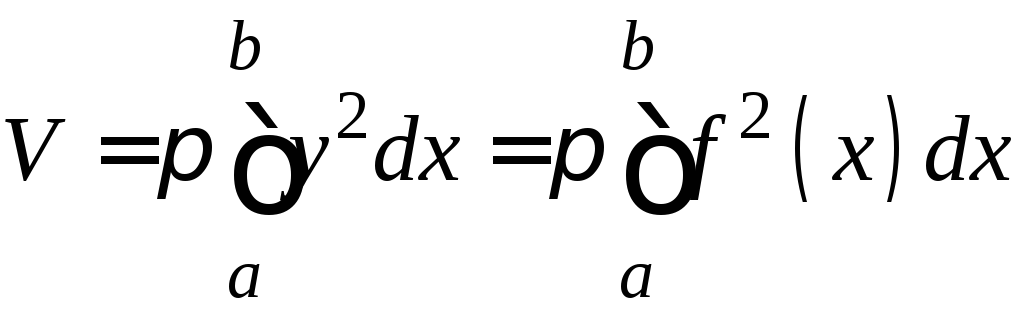 .
.
Если
вращение происходит вокруг оси
![]() ,
то
,
то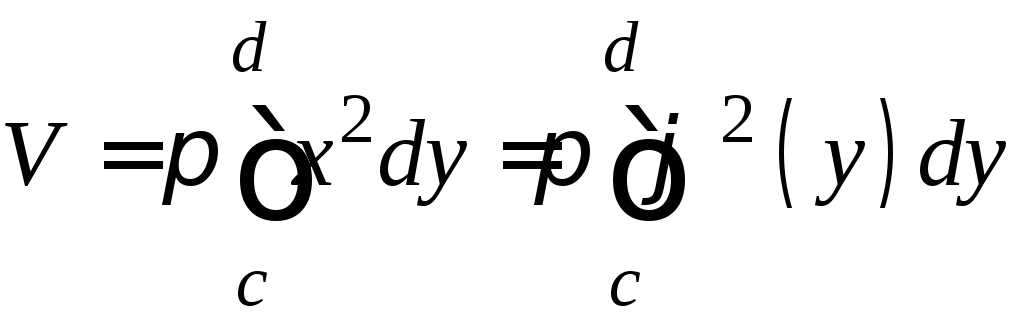 ,
,
где
![]() - уравнение непрерывной кривой,
- уравнение непрерывной кривой,![]() и
и![]() - ограничивающие плоскости.
- ограничивающие плоскости.
П РИМЕР.
Найти объём тела, образованного вращением
фигуры, ограниченной линиями
РИМЕР.
Найти объём тела, образованного вращением
фигуры, ограниченной линиями
![]() ,
,![]() ,
,![]() вокруг оси
вокруг оси![]() (рис. 24).
(рис. 24).
РЕШЕНИЕ
Тело, полученное в результате вращения фигуры (криволинейной трапеции), является параболоидом вращения. Его объём можно вычислить по формуле
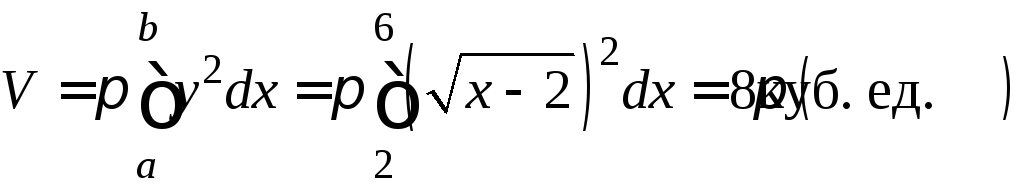 .
.
Тема 4. Дифференциальные уравнения
4.1 Основные понятия
При решении экономических, технических, биологических и других задач за основу берется некоторый общий закон, связывающий бесконечно малые изменения рассматриваемых величин (дифференциальный закон). Уравнения, получаемые при выводе закона, называются дифференциальными.
ОПРЕДЕЛЕНИЕ. Дифференциальное уравнение - это уравнение, связывающее функционально зависимые переменные и их производные (или дифференциалы).
Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком этого уравнения.
Если искомая функция зависит только от одного аргумента, то уравнение называется обыкновенным. Мы будем рассматривать только обыкновенные дифференциальные уравнения.
В
общем случае обыкновенное дифференциальное
уравнение
![]()
![]() –
го порядка может быть записано в виде
–
го порядка может быть записано в виде
![]() ,
,
где
![]() - неизвестная функция,
- неизвестная функция,![]() -
некоторая функциональная зависимость
между независимой переменной
-
некоторая функциональная зависимость
между независимой переменной![]() ,
функцией
,
функцией![]() и ее производными.
и ее производными.
Например:
![]() -
дифференциальное уравнение 1-го порядка,
-
дифференциальное уравнение 1-го порядка,![]() - дифференциальное уравнение 2-го порядка,
- дифференциальное уравнение 2-го порядка,![]() - дифференциальное уравнение 3-го порядка.
- дифференциальное уравнение 3-го порядка.
ОПРЕДЕЛЕНИЕ. Функция, обращающая дифференциальное уравнение в тождество, называется решением этого уравнения.
ПРИМЕР.
Показать, что функции
![]() ,
где
,
где![]() произвольная постоянная, являются
решениями дифференциального уравнения
произвольная постоянная, являются
решениями дифференциального уравнения![]() .
.
РЕШЕНИЕ.
Найдем
первую производную функций
![]() :
: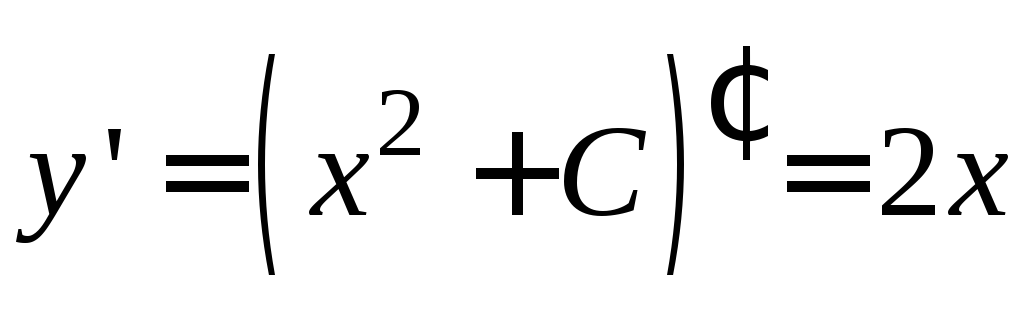 и подставим ее в уравнение. Получим
тождество:
и подставим ее в уравнение. Получим
тождество:![]() ,
т. е. функции
,
т. е. функции![]() являются решениями дифференциального
уравнения. Уже на этом примере, видно,
что дифференциальное уравнение имеет
бесконечное множество решений.
являются решениями дифференциального
уравнения. Уже на этом примере, видно,
что дифференциальное уравнение имеет
бесконечное множество решений.
Процедура отыскания решения называется интегрированием дифференциального уравнения. Если задачу нахождения всех решений дифференциального уравнения удается свести к вычислению конечного числа интегралов и производных от известных функций, а также к алгебраическим операциям, то говорят, что уравнение интегрируется в квадратурах.
В
общем случае решение уравнения
![]() -
го порядка находится в результате
-
го порядка находится в результате![]() последовательных интегрирований,
поэтому решение уравнения содержит
последовательных интегрирований,
поэтому решение уравнения содержит![]() произвольных постоянных. Эту совокупность
решений называютобщим
решением дифференциального уравнения
произвольных постоянных. Эту совокупность
решений называютобщим
решением дифференциального уравнения
![]() -
го порядка
и записывают
в явной
-
го порядка
и записывают
в явной
![]() или неявной
или неявной![]() форме.
форме.
Частным
решением дифференциального уравнения
называют
общее решение, для которого указаны
конкретные значения произвольных
постоянных. Для определения
![]() произвольных
постоянных необходимо задать столько
же условий. Эти условия включают задание
значения функции и ее производных в
определенной точке. Так для уравнения
произвольных
постоянных необходимо задать столько
же условий. Эти условия включают задание
значения функции и ее производных в
определенной точке. Так для уравнения
![]() -
го порядка необходимо задать
-
го порядка необходимо задать
![]() .
.
Числа
![]() называютначальными
значениями,
а равенства – начальными
условиями.
Задача о нахождении частного решения
дифференциального уравнения при заданных
начальных условиях называется задачей
Коши.
называютначальными
значениями,
а равенства – начальными
условиями.
Задача о нахождении частного решения
дифференциального уравнения при заданных
начальных условиях называется задачей
Коши.
