3.4 Несобственные интегралы

Отметим два существенных момента при нахождении определенного интеграла : функциядолжна быть ограничена и промежутокконечен. Рассмотрим случаи, когда эти условия не выполняются.

Несобственный интеграл с бесконечными пределами

Пусть, функция определена на промежуткеи интегрируема на любой его конечной части.

ОПРЕДЕЛЕНИЕ. Несобственным интегралом от функции на промежуткеназывается предел интеграла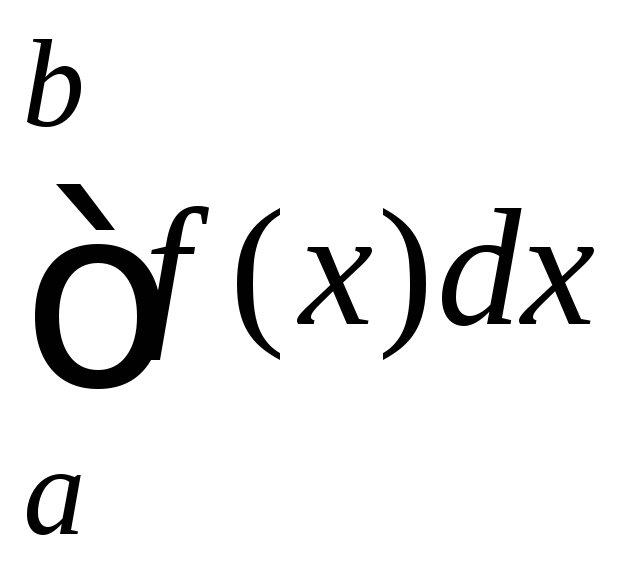, если:

.

Если этот предел конечен, говорят, что интеграл сходится. Если же предел бесконечен или не существует, про интеграл говорят, что он расходится.

Пусть функция – первообразная для функции, тогда можно записать, что.

Введем условное обозначение , получим:

.

Геометрически сходящийся несобственный интеграл , представляет собой площадь фигуры, ограниченной линиями:(рис. 11).

Аналогично рассматривается несобственный интеграл на промежутке .

Тогда несобственный интеграл на промежутке можно определить равенством

,

т.е. .

Несобственный интеграл от неограниченной функции

К другому типу относятся несобственные интегралы, содержащие под знаком интеграла функцию, терпящую разрыв в какой-либо точке из области интегрирования.

Рассмотрим функцию непрерывную для всех значенийв промежуткахи, неограниченную в любой окрестности точкиотрезка.

ОПРЕДЕЛЕНИЕ. Несобственным интегралом от неограниченной функции на промежуткеназывают

.

Если пределы в правой части равенства существуют и конечны, то интеграл называют сходящимся, в противном случае расходящимся.

ПРИМЕР. Вычислить несобственный интеграл (или установить его расходимость).

РЕШЕНИЕ

Степенная функция определена на бесконечном промежуткеи интегрируема на любом конечном промежутке, поэтому

.

Несобственный интеграл расходится.

ПРИМЕР. Вычислить несобственный интеграл .

РЕШЕНИЕ

.

Интеграл сходится.

ПРИМЕР. Вычислить .

РЕШЕНИЕ

В точке подынтегральная функция терпит бесконечный разрыв, поэтому

.

Интеграл расходится.

ПРИМЕР. Вычислить .

РЕШЕНИЕ

В точке подынтегральная функциянеограниченна (рис.12), поэтому проинтегрируем функцию на промежутке, а затем вычислим предел, если:

.

Интеграл сходится. Геометрически это значит, что площадь незамкнутой фигуры, ограниченной линиями , равна 2 кв. ед..

ПРИМЕР. Вычислить несобственный интеграл .

РЕШЕНИЕ

Функция имеет бесконечный разрыв в точке, которая лежит внутри промежутка. Представим исходный интеграл в виде суммы интегралов и вычислим каждый из них. Интеграл сходится, если сходятся оба интеграла в правой части равенства.

,

.

Так как один из интегралов расходится, то можно утверждать, что исходный интеграл расходится.

3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей

1. Р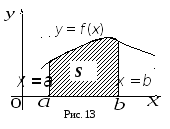ассмотрим фигуру (рис.13), ограниченную линиями,,и, гденепрерывная на отрезкенеотрицательная функция. Площадь такой фигуры вычисляется по формуле

.

2. Если на(рис. 14), то , а так как площадь фигуры есть величина положительная, то

или .

3. Рассмотрим замкнутую фигуру (рис. 15), ограниченную кривыми

, и двумя вертикальными прямымии.

Тогда площадь S можно вычислить как разность площадей криволинейных трапеций:

и ,

т.е. или.

ПРИМЕР. Вычислить площадь фигуры, ограниченной линиями:

(рис. 16).

РЕШЕНИЕ

Используем формулу .

Тогда .

.

ПРИМЕР. Вычислить площадь фигуры, ограниченную линиями и.

РЕШЕНИЕ

Чтобы найти область интегрирования, найдем точки пересечения параболы и прямой. Исключим неизвестную и получим квадратное уравнение

Рис. 17

, ,

.

Следовательно, кривые пересекаются в точках с координатами и.

Используем формулу для вычисления площади фигуры, ограниченной двумя кривыми :

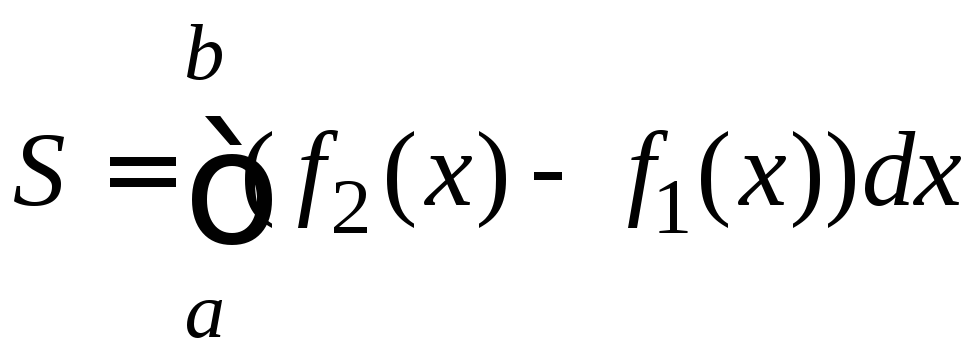Если кривая, ограничивающая криволинейную трапецию, задана параметрическими уравнениями гдеидифференцируемые функции, то

.

Справедливость формулы следует из правила замены переменной в определённом интеграле в предположении, что приипри.

ПРИМЕР. Вычислить площадь эллипса, заданного параметрическими уравнениями:

РЕШЕНИЕ

Эллипс – фигура, симметричная относительно осей координат. Для упрощения вычислений найдем площадь четверти эллипса. Пусть переменная изменяется отдо. Подставимв уравнение, тогда, и. Если, тои, т. е., а. Поэтому площадь равна:

.

Рассмотрим фигуру , ограниченную линией, заданной в полярных координатах, и двумя лучами:и. Функцияположительная и непрерывная для всех, удовлетворяющих неравенству.

Чтобы вычислить площадь криволинейного сектора, разобьём его лучами наэлементарных секторов (см. рис. 19). Криволинейный секторзаменим круговым сектором. Его площадь равна, где- центральный угол кругового сектора,- радиус окружности. Так как мы имеемсекторов, то площадь ступенчатой фигурыравна

.

Увеличивая число разбиений таким образом, чтобы получим, что .

ПРИМЕР.Вычислить площадь фигуры, ограниченную лемнискатой (рис.20).

РЕШЕНИЕ

Воспользуемся симметричностью фигуры и вычислим четвёртую часть площади. Угол изменяется отдо, следовательно, площадь равна

.

Площадь всей фигуры : .
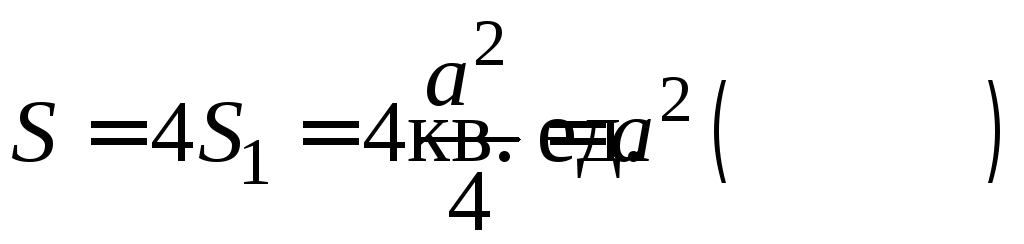