Некоторые типы интегралов, берущиеся посредством формулы интегрирования по частям:

, где  многочлен, действительное число

4. Интегрирование рациональных функций.

А) Метод неопределенных коэффициентов: Интегрирование рациональной функции после выделения целой части сводится к интегрированию правильной рациональной дроби , где целые многочлены, причем степень числителя ниже степени знаменателя. Если, то справедливо следующее разложение:

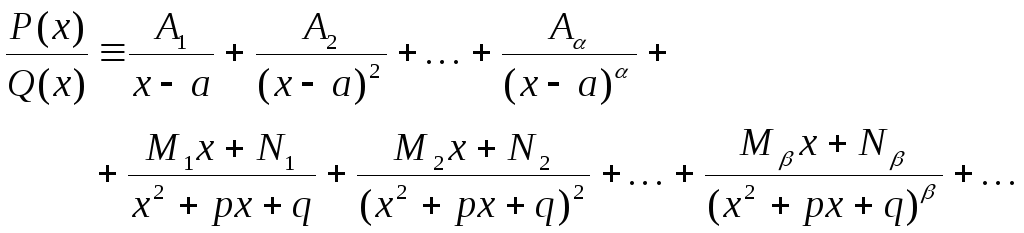
Для вычисления неопределенных коэффициентов ,,обе части тождества приводят к целому виду, а затем приравнивают коэффициенты при одинаковых степенях.

Пример. Найти .

Б) Метод Остроградского: Если имеет кратные корни, то, где общий наибольший делитель многочлена и его производной;; многочлены с неопределенными коэффициентами, степени которых соответственно на единицу меньше степеней и.

Пример. Найти .

5. Интегрирование иррациональных функций.

А) Интегралы вида , где

рациональная функция,  целые числа, находятся с помощью подстановки , где общее наименьшее кратное чисел .

Пример. Найти .

Б) Интегралы вида , где многочлен степени , полагают равными, где многочлен степени с неопределенными коэффициентами; число. Коэффициенты и числонаходят с помощью дифференцирования тождества.

Пример. Найти .

В) Интеграл вида с помощью подстановкиприводят к интегралам вида Б).

Пример. Найти .

Г) Интегралы вида , где рациональные числа, выражаются через конечную комбинацию элементарных функций лишь в случаях:

• если  целое число;

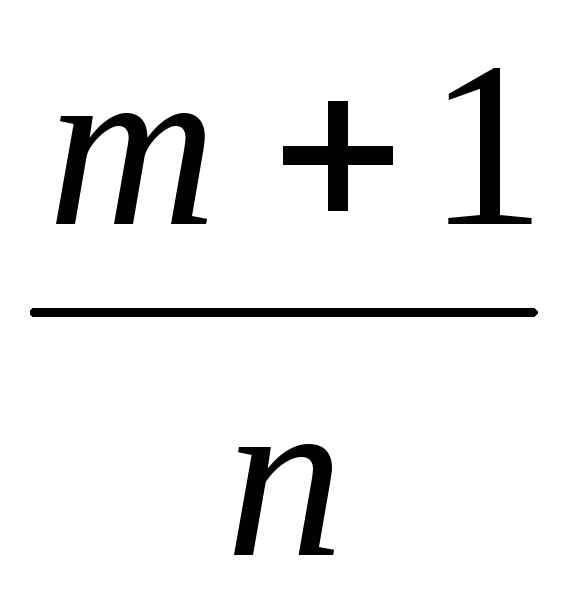
• если  целое число. Тогда используется подстановка , где знаменатель дроби ;

• если  целое число. В этом случае используется подстановка .

Пример. Найти .

6. Интегрирование тригонометрических функций.

А) Для интегралов вида , где целые числа, возможны случаи:

1) Если  нечетное число, то

Аналогично, если  нечетное число.

Пример. Найти .

2) Если ичетные положительные числа, то подынтегральные выражения преобразуются с помощью формул:,,.

Пример. Найти .

3) Если и целые отрицательные числа одинаковой четности, то ,

в частности, ,.

Пример. Найти .

Б) Интегралы вида ,,преобразуются с помощью формул:

,

,

.

Пример. Найти .

В) Для вычисления интегралов вида , где рациональная функция, можно использовать подстановку , откуда.

Пример. Найти .

Если , то можно применить замену переменной, где.

Пример. Найти .

Определенный интеграл.

Пусть на отрезке задана функция(рис. 1). Разобьем отрезок наэлементарных отрезков точками, где. На каждом отрезке разбиения выберем некоторую точкуи положим, где.

Рис. 1.

Сумму вида будем называтьинтегральной суммой для функции на отрезке .

Обозначим через максимальную из длин отрезков, т.е..

Определенным интегралом от функции на отрезкеназывается предел интегральной суммы при, т.е., нижний предел,  верхний предел,  подынтегральная функция,  подынтегральное выражение.

Замечание 1. Переменную под знаком интеграла можно обозначать любой буквой: и т. д.

Замечание 2. В отличие от неопределенного интеграла , который представляет семейство функций (первообразных), определенный интегралесть определенное число.

Теорема (достаточное условие существования определенного интеграла). Если функция непрерывна на отрезке, то она интегрируема на этом отрезке.

Свойства определенного интеграла:

1. Постоянный множитель можно выносить за знак интеграла: .

2. Интеграл от алгебраической суммы 2х функций равен такой же сумме интегралов от этих функций: .

3. При перестановке пределов интегрирования знак определенного интеграла меняется на противоположный: .

4. Если пределы интегрирования равны , то интеграл равен нулю:.

5. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей: .

6. Если на отрезке , где,, то и, т.е. обе части неравенства можно почленно интегрировать.

7. Если на отрезке, то.

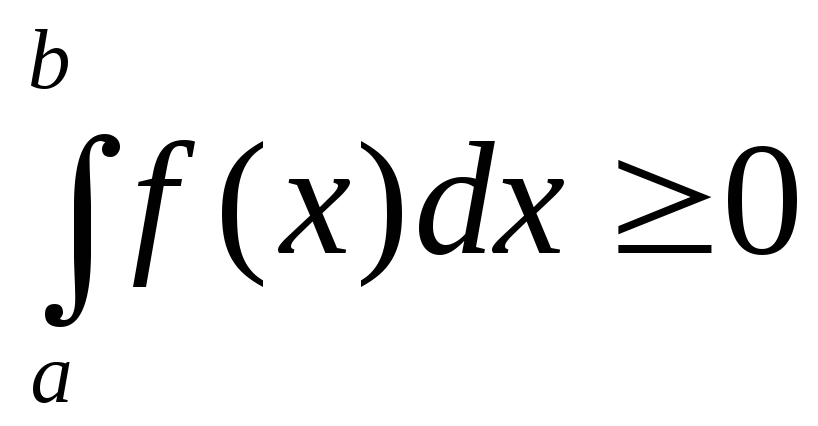8. Если интегрируема на отрезке, то.

9. Теорема о среднем. Если функция непрерывна на отрезке, то найдется такое значение, что. Т.о. теорема о среднем утверждает, что найдется такая точкаиз отрезка, что площадь под кривойравна площади прямоугольника со сторонамии.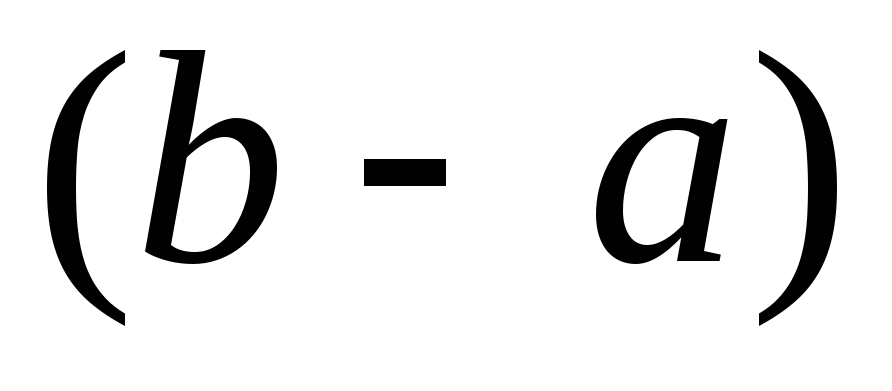

Пусть  непрерывная на отрезке функция, а ее первообразная. Рассмотрим определенный интеграл , где. При изменении меняется и определенный интеграл , т.е. он является функцией верхнего предела интегрирования, которую обозначим через:. Функцияназываетсяинтегралом с переменным верхним пределом (с открытым верхним пределом).

Теорема. Если функция непрерывна на отрезке, то функциятак же непрерывна на.

Теорема о производной интеграла по верхнему пределу. Пусть функция непрерывна на отрезке. Тогда в каждой точкеотрезкапроизводная функциипо переменному верхнему пределу равна подынтегральной функциина верхнем пределе, т.е..

Теорема. Пусть функция непрерывна на отрезкеи любая первообразная для на. Тогда определенный интеграл от функциина отрезкеравен приращению первообразнойна этом отрезке: это формула Ньютона-Лейбница или основная формула интегрального исчисления.

Формула Ньютона-Лейбница позволяет находить определенный интеграл, обходя суммирование, при помощи первообразных функций.

Пример. Вычислите и.

Методы вычисления определенного интеграла:

1. Метод замены переменной (метод подстановки). Данный метод основан на следующей теореме: Пусть дан интеграл , где функция непрерывна на отрезке. Введем новую переменную равенством, где: 1) между переменными и существует взаимно-однозначное соответствие; 2) непрерывна на отрезке ; 3) ; 4) непрерывна на . Тогда .

Пример. Вычислите .

2. Интегрирование по частям. Теорема. Пусть функции ,имеют непрерывные производные на отрезке. Тогда имеет место равенство: эта формула называется формулой интегрирования по частям для определенного интеграла.

Пример. Вычислить .

Геометрические приложения определенного интеграла:

1. Площадь плоской фигуры.

А) Пусть на отрезке задана неотрицательная функция. Тогда площадькриволинейной трапеции, ограниченной кривой, прямымии осью абсцисс(рис. 2) численно равна определенному интегралу от функции на, т.е..

Рис. 2.

Пример. Найти площадь фигуры, ограниченной линиями .

Б) Если функция неположительная и непрерывна на отрезке(рис. 3), то площадь над кривойнаотличается знаком от определенного интеграла, т.е.

Рис. 3.

Пример. Найти площадь фигуры, ограниченной кривой и осью абсцисс.

В) Теорема. Если на отрезке заданы непрерывные функцииитакие, что(рис. 5).

Рис. 5.

Тогда площадь фигуры, заключенной между кривымиина отрезке, вычисляется по формуле:.

Пример. Найти площадь фигуры, ограниченной линиями: .

2. Объем тела вращения:

А) вокруг оси :.

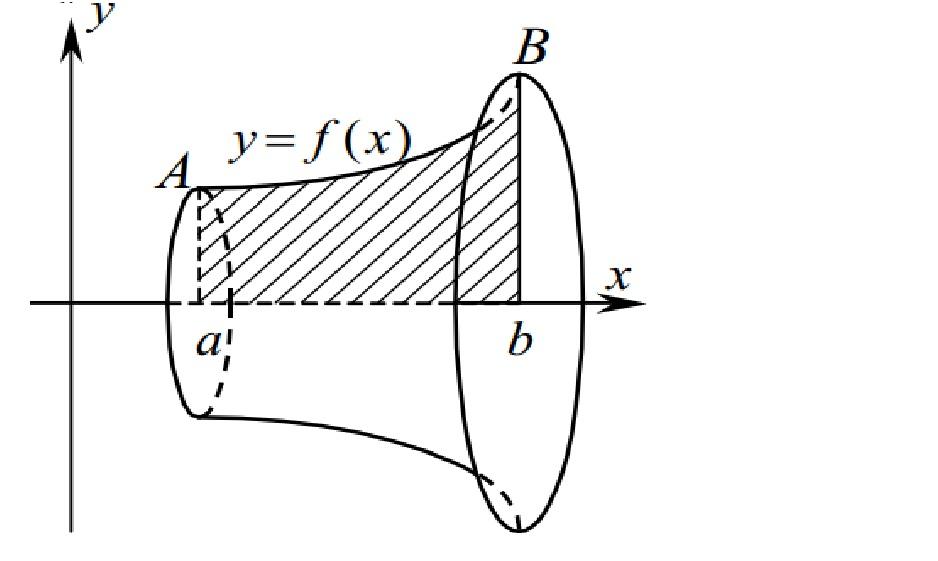
Б) вокруг оси :.

3. Вычисление длины дуги кривой на отрезке : .

4. Вычисление площади поверхности вращения вокруг оси :.

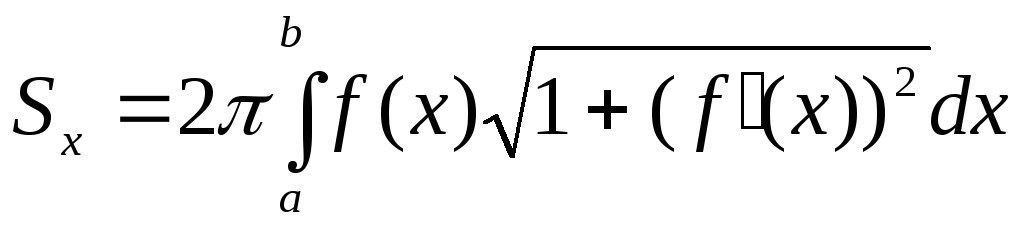Экономический смысл определенного интеграла. Пусть функция описывает изменение производительности некоторого производства с течением времени. Тогда объем продукции, произведенной за промежуток времени, равен.

Физические приложения определенного интеграла:

1. Пройденный путь. Пусть точка движется вдоль некоторой кривой со скоростью . Тогда путь, пройденный точной за время, равен.

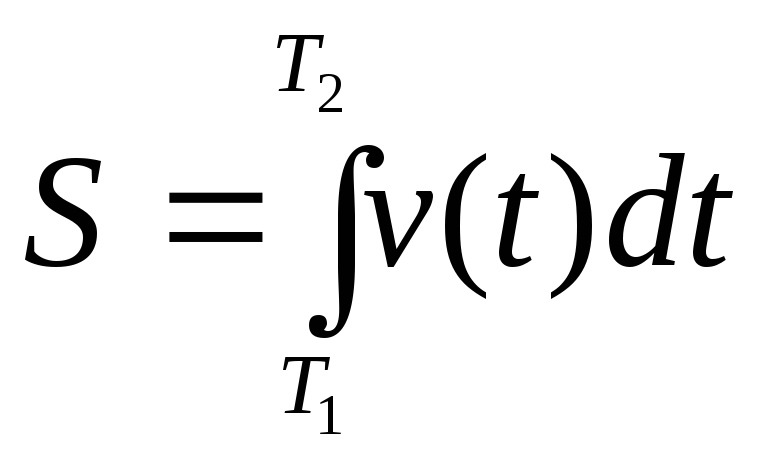2. Масса отрезка. Пусть 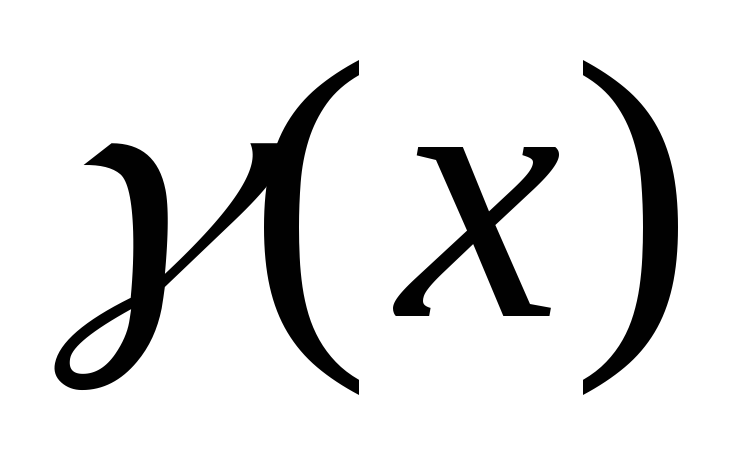– плотность распределения массы на отрезке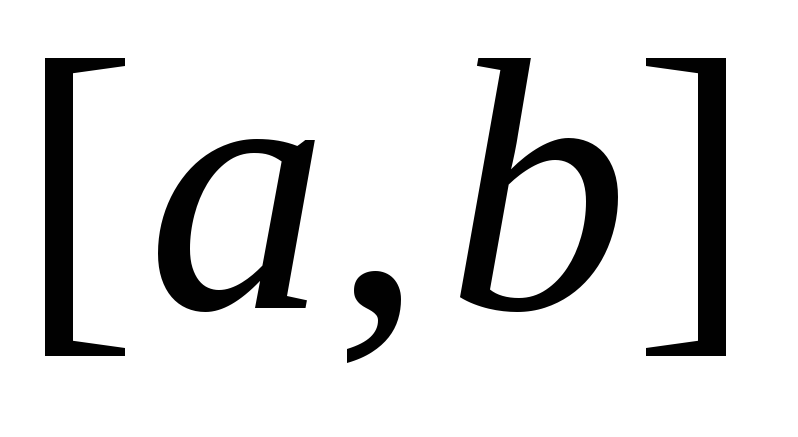. Тогда масса отрезка равна:.

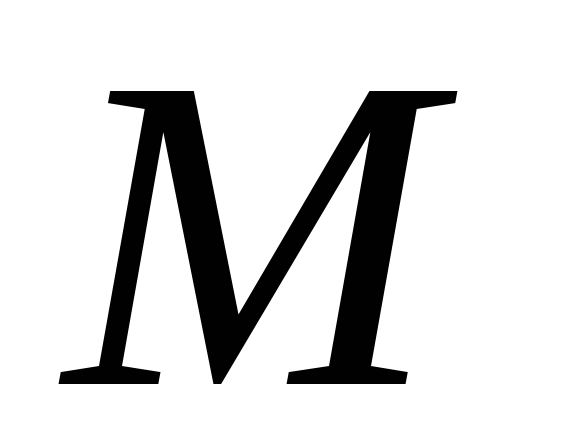3. Работа переменной силы. Пусть под действием некоторой силы материальная точкадвижется по прямой в направлении осииз точкив точку. Тогда работа, произведенная силойпри перемещении точкииз положенияв положениеравна.