техническая электродинам КПИ (Кривець)
.pdf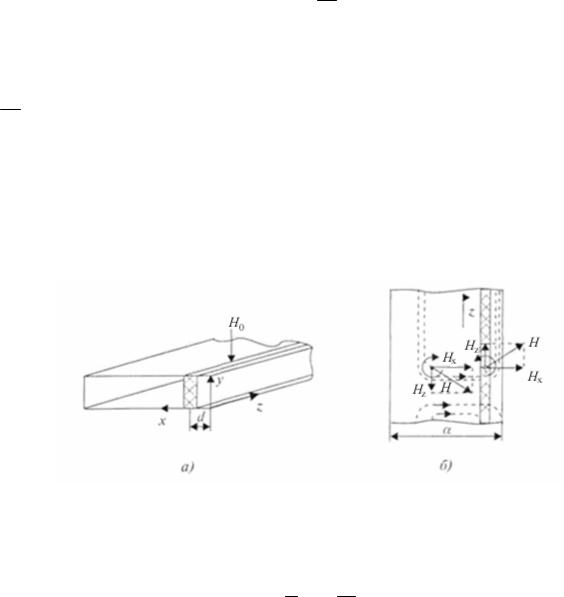

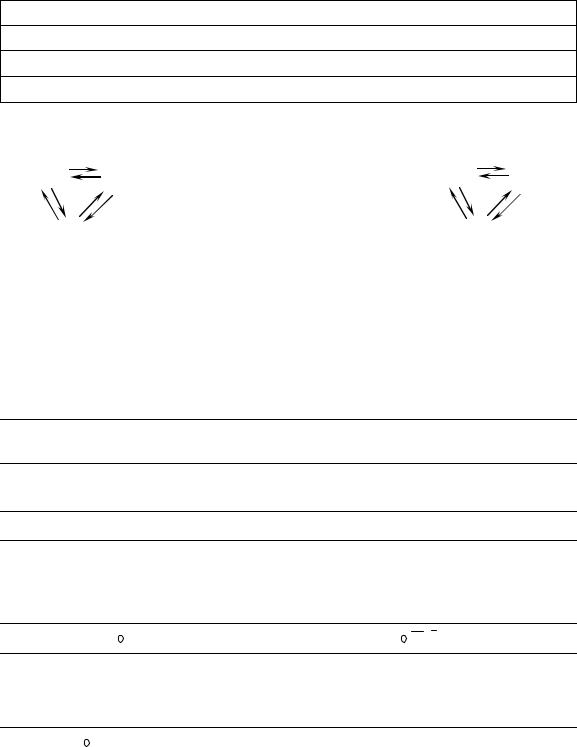
|
Деякі важливі векторні тотжності |
|
Якщо |
divL = 0 , то існує такий вектор M , щоrotMK |
= L |
G |
G |
|
div( A × B) = BrotA − ArotB |
|
|
div(rotA) ≡ 0
rot(rotA) = grad (divA) − A
Основні співвідношення електростатики та магнітного поля постійного струму
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
q(ρ) |
|
|
|
|
E, D |
|
|
|
|
|
|
|
|
|
|
F = qE + q[vG×B] |
|
|
|
|
|
|
|
|
I (J ) |
|
|
|
|
|
|
H , B |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
||||
|
ε = ε0εr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ а = σCиσ r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μ = μr μ0 |
|
|
||||||||||
|
1 |
|
|
−9 |
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
σCи = 5, 7 107 , |
См |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε0 = |
|
10 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
μ0 = 4π 10−7 , |
Гн |
|
||||||||||||||
36π |
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
Закон Ома в диференціальній |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формі: G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J пр = σ E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
q |
|
|
|
q |
|
|
|
|
|
|
|
G |
|
|
|
G |
|
|
|
|
q M |
|
1 q M |
|
|
2 G |
|
|
|
||||||||||
|
|
|
F = |
|
|
1 |
|
|
2 |
|
|
|
1r |
|
|
F M |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 r |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 πμ |
|
r |
2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
4 πε r 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
G |
|
|
q1 q 2 |
|
|
|
G |
|
|
|
|
|
|
G |
|
|
|
IGdlG |
G |
|
|
|
||||||||||||||||||||
|
|
|
F |
= |
|
4 πε r 3 |
|
1r |
, |
|
|
|
|
dH |
= |
|
|
|
|
|
× |
1 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r G2 |
|
|
|
|
|
r |
|
|
|
||||||||||||||||
|
|
|
|
|
EG = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HG = |
FM |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qM |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
G |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
B = μH |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
GD =εE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∫ B dsG = q м = 0 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
∫D dsG = qΣ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
divD = ρ |
|
|
|
|
|
|
|
|
divB = ρм = 0 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
∫EGdlG = 0 |
|
|
|
|
|
|
|
|
|
∫Hdl = IΣ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
G |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
G |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
rotE |
|
|
|
|
|
|
|
|
|
|
|
rotH |
|
= J |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
E = −gradϕ |
|
|
|
|
|
|
G |
|
|
1 |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
= |
|
|
|
rotA |
|
|
|
|
|
|
|
||||||||
|
|
|
ϕ = |
|
|
|
|
+C |
|
|
|
|
|
|
μ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
∫Edl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
G |
|
|
|
|||||
|
|
∫D dS = |
∫divDdV |
|
|
∫H dl = ∫rotH |
dS |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
S |
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2ϕ = − |
|
ρ |
|
|
|
|
|
|
|
|
|
2 A = −μJG |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
∫ |
|
ρ |
|
|
|
|
|
G |
μ |
|
J |
|
|
|
|
|
|
|
μ |
|
|
|
|
I |
G |
|
|
|||||||||
|
|
|
ϕ = |
|
|
|
|
|
dV |
|
|
A = |
|
∫ |
|
dV = |
|
|
|
∫ |
|
dl |
1A |
||||||||||||||||||||||
|
|
|
4πε |
|
|
|
r |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4π |
r |
4π |
|
|
r |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Граничні |
умови |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eτ1 = Eτ 2 |
|
|
|
|
|
|
|
|
Hτ1 − Hτ 2 = Jl |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
214 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|