техническая электродинам КПИ (Кривець)

Розглянемо детально перший інтеграл для фронтальної поверхні. Оскільки елемент поверхні дуже малий, значення D можна вважати незмінним й тоді:

31

Таким чином використано закон Гаусса-Остроградського для обмеженого простору, який оточує елемент об’єму V , і як результат маємо апроксимацію, яка стверджує, що заряд замкнений в об’ємі V дорівнює

Таким чином можна вважати що дивергенція – це диференціальна характеристика потоку .

Формула (2.3-23) визначає закон Гаусса-Остроградського в диференціальній формі.

32

2.3.3 Перетворення (теорема) Гаусса-Остроградського

Це співвідношення отримало назву перетворення (теорема) Гаусса–Остроградського - потік вектора через замкнуту поверхню дорівнює інтегралу від дивергенції цього вектора, взятого за об’ємом, обмеженим цією поверхнею. Тобто воно пов’язує об’ємний інтеграл з поверхневим і дозволяє змінювати порядок інтегрування.

2.4 Робота сил та потенціал електростатичного поля

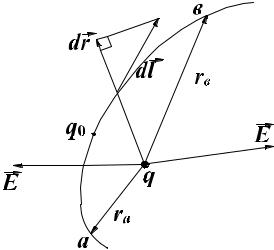
Розглянемо ситуацію таку, що в електростатичному полі точкового заряду q в деякому просторі переміщується пробний заряд q0 за траекторією l (рис. 2.6).

Рисунок 2.6 Траєкторія руху заряду q0 в полі, що створено зарядом q

За законом Кулона на заряд діє сила

Елемент роботи цієї сили dA на ділянці шляху dl (рис. 2.6):

33

Звідки випливає, що робота сил електростатичного поля не залежить від форми шляху, а визначається найкоротшою відстанню між початковою та кінцевими точками. Сили, робота яких не залежить від шляху, називають консервативними.

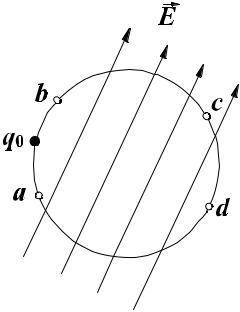
Рисунок 2.7 Замкнутий контур переміщення заряду q0 в полі EG .

Цей висновок для точкового заряду можна узагальнити для будь –якого електростатичного поля. Розглянемо роботу сил електростатичного поля з переміщення заряду q0 по замкнутій траєкторії

abcd (рис 2.7). В даному випадку роботу розрахують інтегруванням E по замкнутому контуру l . Проявом сили, яка Gздійснює роботу, є напруженість поля. В електричному полі цю силу

характеризує вектор E

На ділянці abc поле витрачає енергію, а на cda навпаки заряд віддає енергію полю. Оскільки робота не залежить від форми траєкторії, то можна стверджувати, що

34

де abc i cda – відстані, що починаються і закінчуються в цих самих точках. Цей інтеграл в енергетичному аспекті відповідає принципу збереження енергії.

Робота з перенесення заряду є тільки функцією відстані між початковою та кінцевими точками, тому можливо ввести скалярні параметри поля, які називають потенціалами. Різниця потенціалів між двома точками характеризує роботу сил електростатичного поля (взяту з протилежним знаком) по перенесенню одиниці кількості електрики з однієї точки в іншу:

Одиниця виміру потенціалу - вольт [B]. На відміну від напруженості поля E , яка є функцією точки, потенціал визначається тільки різницею своїх значень в двох точках і є скаляром. Уявімо, що точка знаходиться на нескінченно великій відстані, тобто потенціал в ній дорівнює нулю; відстань до т. b → ∞ , то ϕb → 0 і тоді ϕa характеризує роботу з переміщення

де С- стала інтегрування, яка враховує початкові умови.

Для поля сукупності зарядів сумарний потенціал, у відповідності з принципом суперпозиції (якщо середовище лінійне) дорівнює сумі потенціалів:

потенціалом, то в ньому завжди можна виділити геометричне місце точок з однаковим потенціалом. В тривимірному просторі таку поверхню називають еквіпотенціальною. Таким чином електростатичне поле можна уявити безліччю еквіпотенціальних поверхонь. Щоб визначитиG взаємне розміщення однієї поверхні відносно іншої, а також відносно силових ліній

E , тобто структуруG поля, введемо поняття градієнта потенціалу – характеристику, яка визначає зв’язок між E та ϕ .

Градієнт потенціалу - це вектор, який характеризує ступінь змінення скалярної величини ϕ та направлений у бік її зростання (за нормаллю до відповідної поверхні). Оскільки

найінтенсивніша зміна відповідає найменшій відстані між поверхнями S1 та S2, то вектор градієнта перпендикулярний дотичній еквіпотенціальній поверхні в конкретній точці і направлений до більшого значення. Тобто можна записати:

35

де 1Gn - одиничний вектор вздовж нормалі до поверхні.

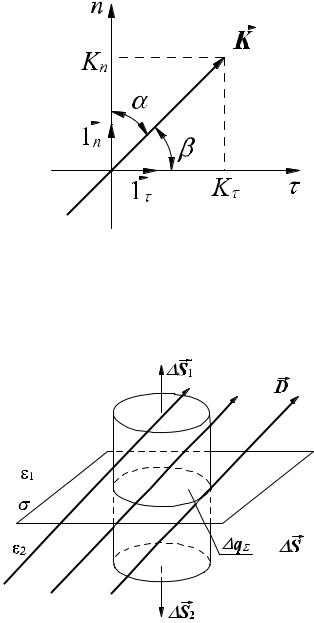
Для визначення градієнту в ортогональній системі координат розглянемо спочатку похідну потенціалу ϕ вздовж довільного напрямку (рис.2.8).

Рисунок 2.8 До визначення градієнта потенціалу

З рис.2.8. визначимо

l = n . (2.5-2)

GG cos(nl )

Візьмемо відношення приросту потенціалу до приросту l :

Вираз (2.5-3а) визначає проекцією вектора gradϕ на довільний напрям l :

36

співвідношенням (2.4-7), в якому за умов зменшення ab в границі dϕ отримаємо:

Це важливе співвідношення свідчить про те, що електричне поле вектора E можна визначити як градієнт скалярної величини – потенціала ϕ . З формули (2.5-9) випливає, що за

відомим значенням потенціалу можна розв’язати пряму задачу електростатики, якщо відомий зв'язок між потенціалом та густиною заряду. Цей зв'язок отримаємо із розв'язку рівняння Пуассона.

2.6Рівняння Пуассона та Лапласа

Для розв'язку прямої задачі електростатики необхідно визначити три проекції вектора E : Ex , Ey , Ez . Це можливо на підставі (2.5-6) та (2.5-9)

37

Таким чином шлях вирішення прямої задачі: за (2.6-4) знайдемо потенціал, як функцію розподілу зарядів відносно координат точки спостереження, а далі за відомим потенціалом визначимо напруженість поля, як градієнт із протилежним знаком (2.5-9).

Якщо в об’ємі, що розглядають, заряди відсутні, то рівняння (2.6-2) та (2.6-3) є:

Формули (2.6-5), (2.6-5а) – це рівняння Лапласа. Їх визначають для розрахунку полів в області простору вільній від зарядів.

Розв’язок рівняння Лапласа визначають як добуток функцій однієї змінної

Підставимо цей розв’язок в початкове рівняння і отримаємо

Перетворимо (2.6-7) таким чином, щоб кожний доданок залежав тільки від однієї змінної:

Тепер можна припустити, що останнє рівняння має розв’язок за умови, що кожний вхідний в нього доданок є величина стала. Далі, для одержання з виразу (2.6-8) системи трьох рівнянь, кожне з яких є функцією змінної, виконаємо такі дії:

- диференціюємо вираз (2.6-8) по x . Отриманий диференціал дорівнює нулю. Це означає, що перший доданок у (2.6-8) є постійною величиною. Позначимо її через K x2 .

-диференціюємо вираз (2.6-8) по y та z . Зробимо висновки про те, що інші доданки в (2.6-

8)теж постійні величини, наприклад, K y2 та K z2 . Вони, відповідно до виразу (2.6-8), зв’язані

рівністю:

Kx2 + K y2 + Kz2 = 0 .

Таким чином, одержимо систему з трьох рівнянь, кожне з яких має лише одну невідому. Перепишемо перше рівняння цієї системи з урахуванням виразу (2.6-8) у вигляді:

38

Та помножимо його на X :

∂2 X − K 2 X = 0 .

∂x2 x

Наведемо одержане рівняння в канонічному вигляді, за якого його розв’язок можна представити через гармонічні функції. Оскільки позначення K x , K y , K z введені довільно, то змінимо їх знаки

на протилежні. Тоді останнє рівняння набуде вигляду:

∂2 X + K 2 X = 0 .

∂x2 x

Його розв’язок буде таким:

де B1 , B2 , C1 , C2 – відповідні сталі.

Підставимо вирази (2.6-9), (2.6-10) і (2.6-11) в (2.6-6) та розв’яжемо рівняння Лапласа. Для цього із введених коефіцієнтів два будемо вибирати довільно, тоді третій буде зв’язаний з цим

Ця уявна величина входить в аргументи тригонометричних функцій – синуса та косинуса. Тоді розв’язок (2.6-11) записується через гіперболічні косинус та синус:

Надалі виникає проблема визначення коефіцієнтів A1 , A2 , B1 , B2 , C1 , C2 , які відповідають

єдиному розв’язку рівняння Лапласа. Тому необхідно розглянути поведінку вектора напруженості електростатичного поля при переході через поверхню розподілу двох середовищ.

39

Єдиному розв’язку конкретної задачі, із безлічі інших розв’язків, буде відповідати такий розв’язок рівняння Лапласа, який водночас задовольняє як саме рівняння, так і граничні умови.

2.7 Граничні умови електростатики

G G

На границі розділу двох середовищ з різними значеннями ε векториD та E можуть бути представлені двома складовими:

-нормальною( проекцією на нормаль до границі)

Рисунок 2.9 Вектор K та його проекції Kn = K cosα , Kτ = K cos β .

2.7.1 Нормальні складові векторів D та E

G

Щоб визначити нормальну складову доцільно вибирати вектор D як такий, що характеризує потік.

Рисунок 2.10 До визначення нормальних складових електричного поля

40