техническая электродинам КПИ (Кривець)

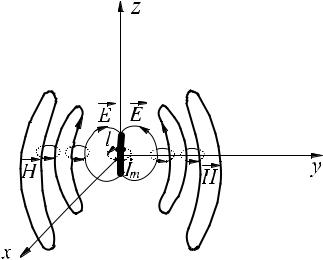
Зауважимо, що у дальній зоні виконуються такі співвідношення:

Ці співвідношення вказують на те, що в дальній зоні інтенсивність загасання електричної та магнітної складових поля однакові (рис.7.4).

Силові лінії складових поля є замкнуті криві, відокремлені від диполя(рис.7.6). Як свідчать рівняння Максвелла змінне в часі електричне поле створює магнітне, магнітне – електричне і т.д..

Таким чином в дальній зоні створено поле внаслідок випромінювання диполем, але не зв’язане з ним безпосередньо.

Рисунок 7.6 Уявлення силових ліній складових дальнього поля

7.1.4 Проміжна зона

Ознакою цієї зони є те, що поле випромінювання, дальнє, та реактивне (зв'язуюче), ближнє, поле характеризується значеннями однакового порядку. Стадії формування силових ліній поля представлено на рис.7.7.

121

в – на цьому етапі заряди зменшуються (спадають); зовнішня частина поля просувається далі, одночасно починають “відшнуровуватись” лінії поля;

ж– струм в межах від 0 до T3 ;

г – в кінці другої чверті періоду обидві половини вібратора не заряджені; “відшнуровування” лінії поля не закінчено;

з – струм в межах від 0 до T2 ;

д – під час третьої частини періоду струм протікає в зворотному напрямку, тому верхня половина вібратора заряджається позитивним зарядом, а нижня – негативним.

к– струм в межах від 0 до 34 T ;

В кінці третьої чверті періоду перейдемо до рисунку аналогічному випадку 2), але лінії поля змінюють напрям і т.д.

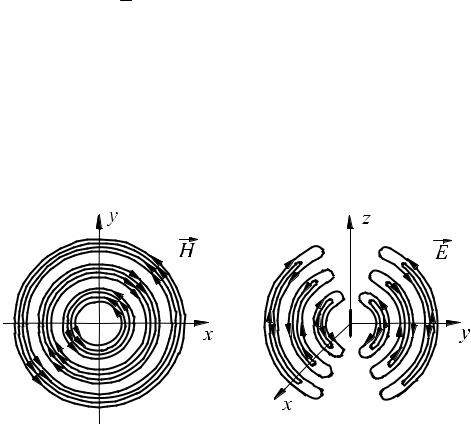
Умовно для диполя Герца лінії електричного поля представлені на рис.7.8б, магнітного поля – на рис.7.8а.

Рисунок 7.8.Силові лінії складових поля: а – магнітного ; б – електричного

7.1.5 Діаграма спрямованості випромінювача

В загальному випадку діаграма спрямованості - це геометричне місце точок однакового значення фізичної величини, в залежності від напряму. В курсі “Технічна електродинаміка” цьому терміну надано такий зміст.

Діаграма спрямованості - це графічне зображення залежності амплітуд векторів поля випромінювання в дальній зоні від кута спостереження.

Випромінювач, електричний вібратор, не випромінює електромагнітне поле вздовж своєї осі, а вздовж осі перпендикулярній до осі вібратора випромінення максимальне. Відповідно до (7.1-15а) можна записати в меридіанній площині (рис.7.9а):

123

В азимутальній площині для складової Hϕ – діаграма спрямованості – круг (рис. 7.7б).

спрямованості. Оскільки в горизонтальній площині Emθ не залежить від ϕ , то діаграма має вигляд тороїда (рис. 7.9в).

Рисунок 7.9 Діаграма спрямованості електричного вібратора: а – в меридіанній площині; б – в азимутній площині; в – об’ємна

7.1.6 Потужність та опір випромінювання диполя Герца

Як вже відомо, потужність хвильового процесу визначють інтегруванням вектора Пойнтінга:

де

124

елементарна площина у сферичній системі координат.

Розглянемо детальніше вектор Пойнтінга і потужність випромінювання. На підставі

(5.2-5) з урахуванням (7.1-24) та (7.1-25а) отримаємо:

125

7.2 Магнітний елементарний випромінювач

7.2.1 Метод вирішення задач

Поле, що утворює елементарний магнітний випромінювач, можна дослідити за методикою аналогічною електричному диполю. Елементарний магнітний випромінювач створимо як аналог електричного вібратора але з магнітним струмом ІM.

Тобто можливо на підставі принципу переставної двоїстості (див. 4.7) виконати відповідні заміни:

Eθ Hθ , Er Hr , Hϕ Eϕ , I −IМ , ε −μ . (7.2-1)

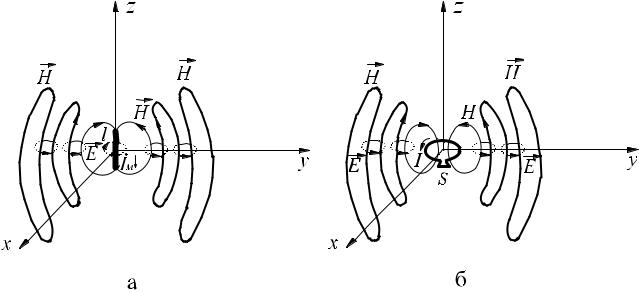
На рис. 7.10а показано електричний вібратор Герца, але з магнітним струмом ІM, який створює силові лінії електромагнітного поля.

Зауважимо, що такі самі лінії поля (відповідно й таке саме поле) формує рамка із електричним струмом (рис.7.10а), замість фіктивного магнітного диполя. Тому реальним магнітним елементарним випромінювачем є рамка із струмом.

Рисунок 7.10 Елементарний магнітний випромінювач: а – з фіктивним магнітним струмом ІM; б – з реальним електричним струмом (рамка зі струмом)

Таким чином систему рівнянь складових електромагнітного поля магнітного елементарного випромінювача для загального вигляду можна отримати із (7.1-12), (7.1-14а), (7.1-15а) відповідно для складових електромагнітного поляEϕ , Hr , Hθ на підставі заміни

126

випромінювач – це рамка із електричним струмом.

Для отримання відповідних формул необхідно виконати заміну фіктивного магнітного

Враховуючи (7.2-5) перепишемо рівняння складових електромагнітного поля магнітного елементарного випромінювача для електричного струму:

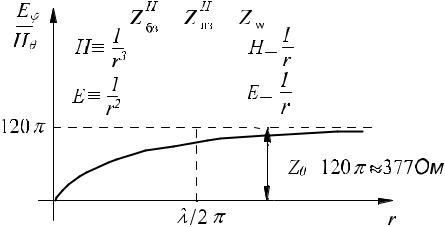
Наведемо формули, що отримані на основі принципу „переставної двоїстості”, за умов ближньої зониr << λ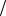2π .

Таблиця 7.1 Складові поля елементарного магнітного випромінювача в ближній зоні

127

Рисунок 7.11 Залежність відношення між складовими E та H від відстані до магнітного випромінювача

Зазначимо, що середнє значення модуля вектора Пойнтінга в ближній зоні дорівнює нулю, як це випливає з (7.2-9) та (7.2-11) або (7.2-12) та (7.2-14), складові Е(t) та Н(t) – в

квадратурі.

Як випливає із (7.2-15) та рис.7.11 параметр ZбзH електромагнітного випромінювача низькоімпедансний.

7.2.3 Дальня зона

Наведемо формули, які отримані на основі принципу „переставної двоїстості” за умови дальньої зониr >> λ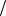2π .

Для дальньої зони запізнення звісно враховують й на підставі наведених вище положень отримаємо формули для лінійного вібратора з фіктивним магнітним струмом (7.2- 16)...(7.2-18) та рамкового, з реальним електричним (7.2-19)...(7.2-21).

Таблиця 7.2 Складові поля елементарного магнітного випромінювача в дальній зоні

128

Звідки також випливає, що з точністю до знака, фази півхвиль Е(t) та Н(t) співпадають, тобто середнє значення вектора Пойнтінга існує – існує процес перенесення електромагнітної енергії.

Визначимо хвильовий опір з (7.2-16) та (7.2-18) або (7.2-19) та (7.2-21):

Для вільного простору μ = μ0 ;ε = ε0 ; Zw =120π ≈ 377 Oм.

Щодо діаграми спрямованості магнітного елементарного випромінювача – вона аналогічна діаграмі диполя Герца, але зорієнтована перпендикулярно.

7.2.4Потужність та опір випромінювання елементарного магнітного випромінювача

Електромагнітне поле, що створюється рамочним випрмінювачем, являє собою просторову локально плоску хвилю, яка переносить потужність в радіальному напряму за

7.3 Елементарний щілинний випромінювач

7.3.1 Метод вирішення задач

Поряд з розглянутими раніше диполем Герца та магнітним елементариним випромінювачем існує так званий елементарний щілинний випромінювач. Ця випромінююча система є бескінечною ідеально провідною площиною, в якій прорізано щілину довжиною l та шириною (рис.7.12).

Рисунок 7.12 Елементарний щілинний випромінювач.

129

Якщо в щілині створити змінне електричне поле, то така щілина стане елементом по якому протікає магнітний струм I M в напрямку паралельному довгим краям щілини.

Для того, щоб дана щілина могла вважатися елементарним випромінювачем, необхідне виконання наступних нерівностей: l << λ , та << l .

У відповідності до принципу переставної двоїстості щілинний випромінювач дуальний по відношенню до електричного випромінювача, тому він є різновидом магнітного випромінювача.

Немає потреби вирішувати нову задачу електродинаміки, використаємо принцип переставної двоїстості до знайдених раніше проекцій векторів поля елементарного електричного випромінювача в дальній зоні:

Слід звернути увагу на те, що в дальній зоні елементарний щільовий випромінювач має електричний вектор з єдиною складовою направленою по орту азимутної координати ϕ. Це

означає, що силові лінії вектора напруженості електричного поля, виходячи з щілини, на деякій відстані приймають форму кіл (рис.4.4б). На практиці в якості величини, що характеризує збуджуюче джерело, замість фіктивного магнітного струму I M зручно

•

використовувати комплексну амплітуду U Щ напруги в щілині, що вимірюється

безпосередньо у вольтах. Врахувавши те, що комплексна амплітуда магнітного струму чисельно дорівнює подвоєній комплексній амплітуді напруги в щілині:

запишемо кінцеві формули для розрахунку проекцій векторів електромагнітного поля в дальній зоні для щілинного випромінювача:

7.3.2Потужність та опір випромінювання елементарного щілинного випромінювача

У відповідності до (7.3-4) та (7.3-5) усереднений за період коливальний вектор Пойнтінга має єдину складову, направлену по радіальному орту:

130