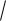Классы, в которых |
Обнаружено детей |
производился |
здоровых |
больных |
всего |
осмотр учащихся |
|
|
|
|
|
|
|
3 и 4 классы |
63 |
92 |
155 |
|
|
|
|
5 и 6 классы |
71 |
39 |
110 |
|
|
|
|
всего |
134 |
131 |
265 |
|
|
|
|
3.3. Проверка гипотез о значимости коэффициентов взаимосвязи
Статистическая проверка гипотез о числовых значениях параметров осуществляется по схеме, описанной в главе 2 (2.1):
В таблице 5 приведены критерии проверки гипотез о значимости коэффициента Фехнера, коэффициента ранговой корреляции Спирмена, коэффициентов ассоциации и контингенции, коэффициентов взаимной сопряженности Пирсона и Чупрова, коэффициента ранговой корреляции Кендала и коэффициента конкордации Кендала.
Задачи
3.1Для коэффициентов взаимосвязи, вычисленным для задач 1.1.- 1.3, проверьте гипотезы о значимости этих коэффициентов.
3.2Для коэффициентов взаимосвязи, вычисленным для задач 2.1.- 2.4, проверьте гипотезы о значимости этих коэффициентов.
Y f X1 , X2 ,..., Xk ε ,
3.4. Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ – это статистический метод анализа выборочных наблюдений, предназначенный для выявления взаимосвязи между количественными признаками. Предполагается, что на формирование средних значений результативного признака Y возможно оказывают влияние факторные признаки X1 , X2 ,...,Xk . При этом наблюдения над признаком Y
должны быть независимыми, выборочная совокупность должна быть достаточно однородной в отношении изучаемого признака и подчиняться нормальному закону распределения вероятностей по результативному и факторным признакам.
Задача состоит в том, чтобы:
1)определить, какое влияние оказывают факторные признаки на результативный признак, насколько тесно они связаны между собой (корреляционный анализ);
2)установить аналитическое выражение связи, выбрать наилучшую модель (регрессионный анализ).
Строится статистическая модель:
где Y – наблюдаемые значения результативного признака;
f X1 , X2 ,..., Xk – аналитическое выражение для определения средних значений признака Y ; ε – случайные отклонения.
Линейный регрессионный анализ заключается в подборе прямой для набора наблюдений с помощью метода наименьших квадратов. Линейная статистическая модель имеет вид:
Y α0 α1 X1 α2 X2 ... αk Xk ε ,
где α0 ,α1,…,αk – параметры уравнения регрессии; ε – случайное отклонение.
По выборке находят оценки a0 ,a1 ,a2 ,...,ak параметров
α0 ,α1 ,α2 ,...,αk . Тогда функция регрессии будет иметь вид:
203
ˆ |
a0 a1 X1 a2 X2 ... ak Xk . |
Y |
Факторные признаки могут иметь различные единицы измерения. Чтобы избежать суммирования величин разной размерности функцию регрессии представляют в стандартизированном масштабе:
ZY b1 Z X1 b2 Z X2 ... bk Z Xk ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Z |
Y Y |
|
, |
Z |
X i |
|
Xi Xi |
- стандартизированные переменные, |
|
|
|
Y |
σY |
|
|
|
|
σ X i |
|
|
|
|
|
|
|
|
bi - стандартизированные коэффициенты регрессии.
Стандартизированный коэффициент регрессии bi
показывает, на какую часть своего среднего квадратического отклонения
σY |
изменится результативный признак Y , если фактор |
X i увеличится |
на |
σX |
при неизменном влиянии прочих |
факторов |
модели. Связь |
|
|
i |
|
|
|
|
|
|
|
коэффициентов множественной регрессии ai |
со стандартизированными |
коэффициентами описывается соотношением: |
a |
|
b |
σY |
. |
|
|
|
|
|
|
i |
|
i σ X |
i |
|
|
|
|
|
|
|
|
Для того, чтобы выяснить, насколько процентов в среднем изменится результативный признак Y , если факторный признак X i
увеличится на 1% от своего среднего уровня при неизменных значениях остальных факторов, рассчитывают средние коэффициенты
|
|
|
|
|
|
|
|
|
|
|
|
эластичности: |
E |
i |
Y a |
i |
Xi |
. |
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты |
эластичности и стандартизированные частные |
коэффициенты регрессии можно использовать для ранжирования факторов по силе влияния на результат. Чем больше величина Ei Y
или bi , тем сильнее влияет фактор X i на результат Y .
Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным и осуществляют на основе
204
2ˆ
Y
анализа остатков: ei yi yˆi , где yi - i-ое наблюдаемое значение результативного признака, yˆi - расчетное i-ое значение результативного
признака, полученное на основе функции регрессии. Отношение
(дисперсии признака Y , «объясненную» уравнением регрессии) к общей дисперсии результативного признака σY2 называют коэффициентом
|
|
R2 |
2ˆ |
|
2 |
|
|
детерминации: |
Y |
1 |
e |
, |
|
2 |
|
|
|
|
2 |
|
|
|
|
Y |
|
Y |
|
|
где σe2 - дисперсия остатков. |
|
|
|
|
|
Проверка значимости уравнения регрессии осуществляется с
помощью критерия Фишера: выдвигают основную гипотезу H |
0 |
: R2 0 о |
|
|
|
|
|
|
|
|
|
|
|
незначимости уравнения в целом и альтернативную ей гипотезу H1 : |
R2 0 о значимости уравнения. Эмпирическое значение F -статистики: |
F |
|
|
|
R2 |
|
|
n k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
эмп |
1 |
R2 |
|
k |
|
|
|
|
|
|
|
|
|
сравнивают с критическим значением Fкр α,γ1 ,γ2 , где |
|
α =0,05 |
– |
уровень значимости; |
γ1 k , |
γ2 |
n k 1 - степени |
свободы |
распределения Фишера-Снедеккора. Если Fэмп Fкр α,γ1 ,γ2 , |
то |
гипотезу о незначимости отвергают.
Оценку качества построенной модели дает также средняя ошибка
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
|
y |
yˆ |
|
|
|
|
|
аппроксимации: |
A |
|
|
|
|
i |
i |
|
|
100. |
|
|
|
|
|
|
n i 1 |
|
|
|
yi |
|
|
|
|
|
|
|
|
Допустимый предел значений A - не более 8-10%.
det R
det R
Для количественной оценки взаимосвязи двух наборов данных, представленном в безразмерном виде, используется парный коэффициент корреляции rij :
r |
cov Xi , X j |
|
, |
|
ij |
si s j |
|
|
|
где cov Xi , X j - ковариация факторов X i |
и X j , si и s j - выборочные |
средние квадратические отклонения этих факторов.
Из парных коэффициентов корреляций составляется
корреляционная матрица:
|
X1 |
X 2 |
X 3 |
… |
X k |
X1 |
1 |
|
|
|
|
X 2 |
r21 |
1 |
|
|
|
X 3 |
r31 |
r32 |
1 |
|
|
: |
: |
: |
: |
: |
: |
|
|
|
|
|
|
X k |
rk1 |
rk 2 |
rk 3 |
… |
1 |
При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной связанности. Считается, что две переменные явно
коллинеарны, если rij 0,7. |
|
|
|
|
По величине парных коэффициентов корреляции обнаруживается |
лишь |
явная |
коллинеарность |
факторов. |
Для |
оценки |
мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами det R . Чем ближе к 0, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1, тем меньше мультиколлинеарность факторов.
xi , yi
Для проверки основной гипотезы |
H0 : det R 1 вычисляют |
эмпирическое значение статистики: |
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
χэмп n 1 |
|
|
5 |
lg |
det R |
|
|
|
2k |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и сравнивают его с критическим значением.
|
2 |
2 |
|
1 |
|
|
|
|
Если χэмп χкр |
α, |
|
n n 1 |
, то гипотеза |
H0 - отклоняется. Для |
|
2 |
|
|
|
|
|
|
|
|
небольших выборок ( n 15 ) критическое значение находят по таблицам,
а для выборок большего объема χкр2 12 1,96 
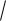2n - 1 2 .
Другая проблема, которая может возникнуть при построении модели множественной регрессии – наличие гетероскедастичности.
Это значит, что для каждого значения фактора X i остатки εi имеют различную дисперсию. Для проверки на наличие гетероскедастичности можно использовать тест Голфелда-Квандта (при небольшом объме выборки), либо тест ранговой корреляции Спирмена.
Рассмотрим однофакторную модель. Пусть имеется n наблюдений над двумя признаками X и Y . Их наблюдаемые значения
можно представить в виде точек на плоскости. Полученное множество точек («облако точек») называется корреляционным полем. Визуальный анализ расположения этого «облака» позволяет сформулировать гипотезу о наличии и форме связи между признаками.
Для оценки тесноты линейной связи между факторным и
результативным признаками X и |
Y |
вычисляют выборочный |
коэффициент корреляции: |
|
|
|
|
|
____ |
__ |
__ |
|
r |
x y x y |
. |
x y |
|
|
|
|
Статистическая оценка средних значений результативного признака
Y в зависимости от различных значений факторного признака X
называется парной регрессией: Y f X . Различают линейные и нелинейные регрессии.
Линейная регрессия: Y a0 a1 X ε (по значениям выборочного коэффициента корреляции и оценке средних значений факторного и результативного признаков можно получить уравнение регрессии:
ˆy r |
|
σY |
x x y ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ X |
|
|
|
|
|
|
|
|
|
|
|
Нелинейные регрессии: |
|
|
|
|
|
|
полиномы Y a |
a |
X a |
|
X 2 |
... a |
k |
X k ε; |
|
0 |
1 |
2 |
|
|
|
|
гипербола Y a0 |
|
a1 |
|
ε; |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
степенная Y a |
X a1 ε; |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
показательная Y a a X ε; |
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
экспоненциальная Y ea0 a1 X ε; |
|
|
|
|
полулогарифмическая Y a0 |
a1 ln X ε; |
|
|
обратная Y |
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
a0 a1 X ε |
|
|
|
|
|
Задачи для самостоятельного решения
4.1 Имеются данные о личном доходе и личных сбережениях в
Великобритании (в млрд. ф. ст.): |
Постройте |
|
|
|
|
|
|
|
|
|
Год |
Доход, X |
Сбережения, Y |
корреляционное |
поле. |
|
1946 |
8,8 |
0,36 |
|
|
|
|
|
1947 |
9,4 |
0,21 |
Сделайте |
|
|
|
1948 |
10,0 |
0,08 |
предположение |
о |
|
1949 |
10,6 |
0,20 |
|
|
|
|
|
1950 |
11,0 |
0,10 |
характере зависимости. |
|
1951 |
11,9 |
0,12 |
Определите |
|
тесноту |
|
1952 |
12,7 |
0,41 |
|
|
|
|
|
|
1953 |
13,5 |
0,50 |
взаимосвязи |
|
между |
|
1954 |
14,3 |
0,43 |
признаками. |
Проверьте |
|
1955 |
15,5 |
0,59 |
|
значимость |
|
|
|
1956 |
16,7 |
0,90 |
|
|
|
|
|
|
|
1957 |
17,7 |
0,95 |
коэффициента |
|
|
1958 |
18,6 |
0,82 |
взаимосвязи |
на |
уровне |
|
1959 |
19,7 |
1,04 |
|
|
|
|
|
1960 |
21,1 |
1,53 |
значимости |
α =0,05. |
|
1961 |
22,8 |
1,94 |
|
Получите |
уравнение |
|
1962 |
23,9 |
1,75 |
|
|
|
|
|
1963 |
25,2 |
1,99 |
регрессии. |
|
|
|
|
|
|
|
|
4.2. Изучается зависимость стоимости одного экземпляра книг (руб.Y ) от тиража (тыс. экземпляров, X ) по следующим данным:
X |
1 |
2 |
3 |
5 |
10 |
20 |
30 |
50 |
|
|
|
|
|
|
|
|
|
Y |
9,10 |
5,30 |
4,11 |
2,83 |
2,11 |
1,62 |
1,41 |
1,30 |
|
|
|
|
|
|
|
|
|
Сделайте предположение о характере зависимости. Постройте модели, выберите лучшую, оцените значимость коэффициентов регрессии.
4.3. Имеются данные по странам за 1994 г. о душевом доходе (по паритету покупательной способности валют) - X (долл.), индексе человеческого развития - Y1 , индексе человеческой бедности - Y2 .
1)Получите описательные статистики. Проверьте характер распределения признаков. При необходимости удалите аномальные наблюдения.
2)Постройте матрицу парных коэффициентов корреляции.
3)Постройте парные линейные уравнения регрессии, принимая душевой доход в качестве объясняющей переменной. Постройте графики остатков. Сделайте выводы.
4)Оцените значимость уравнений регрессии в целом и их параметров. Сравните полученные результаты, выберите лучшую модель.
Страна |
X |
Y1 |
Y2 |
ОАЭ |
1600 |
0,866 |
14,9 |
Таиланд |
7100 |
0,833 |
11,7 |
Уругвай |
6750 |
0,883 |
11,7 |
Ливия |
6130 |
0,801 |
18,8 |
Колумбия |
6110 |
0,848 |
10,7 |
Иордания |
4190 |
0,730 |
10,9 |
Египет |
3850 |
0,514 |
34,8 |
Марокко |
3680 |
0,566 |
41,7 |
Перу |
3650 |
0,717 |
22,8 |
Шри-Ланка |
3280 |
0,711 |
20,7 |
Филиппины |
2680 |
0,672 |
17,7 |
Боливия |
2600 |
0,589 |
22,5 |
Китай |
2600 |
0,626 |
17,5 |
Зимбабве |
2200 |
0,513 |
17,3 |
Пакистан |
2150 |
0,445 |
46,8 |
Уганда |
1370 |
0,328 |
41,3 |
Нигерия |
1350 |
0,393 |
41,6 |
Индия |
1350 |
0,446 |
36,7 |
