
- •Для экзамена
- •Условие изоморфизма конечномерных линейных пространств
- •Матрица перехода к новому базису, изменение координат вектора.
- •Линейные подпространства, размерность линейной оболочки,
- •Формула для размерности суммы двух подпространств
- •Прямая сумма подпространств, различные определения
- •Линейное отображение векторных пространств, ядро и образ.
- •Матрица линейного отображения (оператора), переход к новому
- •Различные характеризации невырожденного оператора
- •Собственные векторы и собственные значения линейного оператора, способы их нахождения. Диагонализируемость оператора с простым спектром.
- •"Поднятие" характеристического и минимального многочленов с ограничений оператора на инвариантных прямых слагаемых.
- •Сопряженное пространство, дуальные базисы, второе сопряженное пространство
- •Билинейные функции и формы, изменение матрицы при переходе
- •Алгоритм Лагранжа для приведения квадратичной формы к
- •Закон инерции вещественных квадратичных форм.
- •Положительно определенные квадратичные функции. Критерий Сильвестра.
- •Евклидовы пространства, условие изоморфизма.( не точно!)
- •Неравенство Коши-Буняковского. Модуль вектора, расстояние и косинус угла между векторами.
- •Процесс ортогонализации Грама-Шмидта
- •Ортогональное дополнение к подпространству евклидова
- •Ортогональные операторы и ортогональные матрицы. (не весь!)
- •Простейший вид матрицы ортогонального оператора евклидова
- •Существование ортогонального базиса из собственных
- •Норма оператора. Норма симметрического оператора.
- •Приведение квадратичной формы ортогональным
- •Приведение пары форм к диагональному виду
- •Число обусловленности матрицы. Связь с приближенным
-
Простейший вид матрицы ортогонального оператора евклидова
пространства.
1 вариант. Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и zиз L и любого действительного числа α справедливы следующие аксиомы:
(x, y) = (y, x),
(α·x, y) = α·(x, y),
(x + y, z) =(x, z) + (y, z),
(x, x)> 0 при x ≠ 0, (0, 0) = 0,
то в пространстве L определено скалярное произведение (x, y).
Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.
2
вариант. Для
определения евклидова пространства
проще всего взять в качестве основного
понятие скалярного
произведения.
Евклидово векторное пространство
определяется как конечномерное векторное
пространство над полем вещественных
чисел,
на векторах которого задана вещественнозначная
функция ![]() обладающая
следующими тремя свойствами:
обладающая
следующими тремя свойствами:
-
Билинейность: для любых векторов
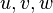 и
для любых вещественных чисел
и
для любых вещественных чисел 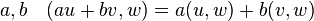 и
и 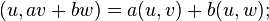
-
Симметричность: для любых векторов
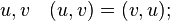
-
Положительная определённость: для любого
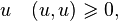 причём
причём 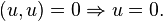
-
Существование ортогонального базиса из собственных
векторов симметрического оператора
Линейный
оператор ![]() называется
симметрическим, если для любых
векторов
называется
симметрическим, если для любых
векторов ![]() выполняется
выполняется ![]() .
.
Перечислим
основные свойства симметрического
линейного оператора:
1. Линейный
оператор является симметрическим тогда
и только тогда, когда его матрица в любом
базисе симметрична.
2. Собственные
векторы симметрического линейного
оператора, соответствующие различным
собственным значениям, ортогональны.
3.Всякому
собственному числу кратности k
симметрического оператора соответствует
линейно независимая система из k
собственных векторов.
4.Для всякого
симметрического линейного оператора
существует базис в пространстве![]() ,
состоящий из его собственных векторов
,
состоящий из его собственных векторов
-
Норма оператора. Норма симметрического оператора.
Норма оператора ![]() — число,
которое определяется, как:
— число,
которое определяется, как:
![]() ,
,
где ![]() — оператор,
действующий из нормированного
пространства
— оператор,
действующий из нормированного
пространства ![]() в нормированное
пространство
в нормированное
пространство ![]() .
.
Это определение эквивалентно следующему:
![]()
-
Свойства операторных норм:
-
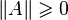 ,
причём
,
причём  только
при
только
при 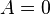 ;
; -
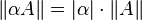 ,
где
,
где 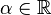 ;
; -
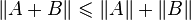 ;
; -
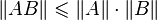 .
.
В конечномерном случае, оператору в некотором базисе соответствует матрица — матрица оператора. Если норма на пространстве(пространствах), где действует оператор, допускает одно из стандартных выражений в базисе, то свойства нормы оператора повторяют аналогичные свойства нормы матрицы.
-
Приведение квадратичной формы ортогональным
преобразованием к главным осям
Рассмотрим
квадратичную форму ![]() .
Матрица A
является
симметричной. Линейное преобразование,
заданное матрицей A,
является самосопряженным и для этого
преобразования существует ортонормированный
базис из собственных векторов. Другими
словами, найдется ортогональная
матрица T (
.
Матрица A
является
симметричной. Линейное преобразование,
заданное матрицей A,
является самосопряженным и для этого
преобразования существует ортонормированный
базис из собственных векторов. Другими
словами, найдется ортогональная
матрица T (![]() ),
что
),
что ![]() ,
где
,
где ![]() -
собственные числа A.
Поскольку
-
собственные числа A.
Поскольку ![]() ,
то квадратичная форма
,
то квадратичная форма ![]() ортогональной
заменой
ортогональной
заменой ![]() переходит
в форму
переходит
в форму![]() .
Приведение квадратичной формы к
каноническому виду ортогональным
преобразованием называется приведением
к главным осям.
.
Приведение квадратичной формы к
каноническому виду ортогональным
преобразованием называется приведением
к главным осям.
