
- •Для экзамена
- •Условие изоморфизма конечномерных линейных пространств
- •Матрица перехода к новому базису, изменение координат вектора.
- •Линейные подпространства, размерность линейной оболочки,
- •Формула для размерности суммы двух подпространств
- •Прямая сумма подпространств, различные определения
- •Линейное отображение векторных пространств, ядро и образ.
- •Матрица линейного отображения (оператора), переход к новому
- •Различные характеризации невырожденного оператора
- •Собственные векторы и собственные значения линейного оператора, способы их нахождения. Диагонализируемость оператора с простым спектром.
- •"Поднятие" характеристического и минимального многочленов с ограничений оператора на инвариантных прямых слагаемых.
- •Сопряженное пространство, дуальные базисы, второе сопряженное пространство
- •Билинейные функции и формы, изменение матрицы при переходе
- •Алгоритм Лагранжа для приведения квадратичной формы к
- •Закон инерции вещественных квадратичных форм.
- •Положительно определенные квадратичные функции. Критерий Сильвестра.
- •Евклидовы пространства, условие изоморфизма.( не точно!)
- •Неравенство Коши-Буняковского. Модуль вектора, расстояние и косинус угла между векторами.
- •Процесс ортогонализации Грама-Шмидта
- •Ортогональное дополнение к подпространству евклидова
- •Ортогональные операторы и ортогональные матрицы. (не весь!)
- •Простейший вид матрицы ортогонального оператора евклидова
- •Существование ортогонального базиса из собственных
- •Норма оператора. Норма симметрического оператора.
- •Приведение квадратичной формы ортогональным
- •Приведение пары форм к диагональному виду
- •Число обусловленности матрицы. Связь с приближенным
-
Сопряженное пространство, дуальные базисы, второе сопряженное пространство
Сопряженное пространство
Для
линейных функционалов на линейном
пространстве ![]() можно
определить операции сложения и умножения
на число:
можно
определить операции сложения и умножения
на число:
Эти
определения удовлетворяют аксиомам
линейного пространства. То есть,
совокупность всех линейных функционалов
на ![]() также
образует линейное пространство. Это
пространство называетсясопряжённым к
также
образует линейное пространство. Это
пространство называетсясопряжённым к ![]() ,
оно обычно обозначается
,
оно обычно обозначается ![]() .
В конечномерном случае сопряжённое
пространство
.
В конечномерном случае сопряжённое
пространство ![]() имеет
ту же размерность что
и пространство
имеет
ту же размерность что
и пространство ![]() .
Обычно элементы пространства
.
Обычно элементы пространства ![]() обозначают
вектором-строкой, а элементы
обозначают
вектором-строкой, а элементы ![]() —
вектором-столбцом. В тензорном
исчислении применяется
обозначение
—
вектором-столбцом. В тензорном
исчислении применяется
обозначение ![]() для
элементов
для
элементов ![]() (верхний,
или контравариантный индекс)
и
(верхний,
или контравариантный индекс)
и ![]() для
элементов
для
элементов ![]() (нижний,
или ковариантный индекс).
(нижний,
или ковариантный индекс).
Верно
также что пространство, сопряжённое к
сопряжённому ![]() ,
совпадает с
,
совпадает с ![]() .
.
Второе сопряженное пространство
ВТОРОЕ СОПРЯЖЕННОЕ ПРОСТРАНСТВО - пространство X'', сопряженное к пространству X', сопряженному к отделимому локально выпуклому пространству X, наделенному сильной топологией. Каждый элемент х ∈ Х порождает элемент F ∈ X'' по формуле F(f) = f(x) (f ∈ X'). Если X'' = X, то пространство X наз. рефлексивным. Если X - бочечное пространство, то линейное отображение π : x → F является изоморфным вложением пространства X в пространство X'', наделенное сильной топологией. Вложение π наз. каноническим. Для нормированных пространств π есть изометрическое вложение.
Дуальный базис
ДВОЙСТВЕННЫЙ БАЗИС, дуальный базис, к базису {е1, ..., еn} модуля Е относительно формы f - такой базис {c1, ..., cn} модуля Е, что
f(ei, ci) = 1, f(ei, cj) = 0, i ≠ j, 1 ≤ i, j ≥ n,
-
Билинейные функции и формы, изменение матрицы при переходе
к новому базису.

Билинейной формой называется функция B : V × V → F, удовлетворяющее свойствам B(αu + βv, w) = αB(u, w) + βB(v, w) и B(w, αu + βv) = αB(w, u) + βB(w, v). Билинейная форма B называется симметричной, если B(u, v) = B(v, u) для любых u, v ∈ V .
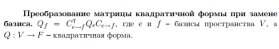
-
Алгоритм Лагранжа для приведения квадратичной формы к
диагональному виду.
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть
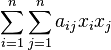
есть данная квадратичная форма. Возможны два случая:
-
хотя бы один из коэффициентов
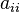 при
квадратах отличен от нуля. Не нарушая
общности, будем считать
при
квадратах отличен от нуля. Не нарушая
общности, будем считать 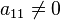 (этого
всегда можно добиться соответствующей
перенумерацией переменных);
(этого
всегда можно добиться соответствующей
перенумерацией переменных); -
все коэффициенты
 ,
но есть коэффициент
,
но есть коэффициент 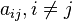 ,
отличный от нуля (для определённости
пусть будет
,
отличный от нуля (для определённости
пусть будет 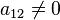 ).
).
В первом случае преобразуем квадратичную форму следующим образом:
![]()
![]()
![]()
где ![]() ,
а через
,
а через ![]() обозначены
все остальные слагаемые.
обозначены
все остальные слагаемые. ![]() представляет
собой квадратичную форму от n-1 переменных
представляет
собой квадратичную форму от n-1 переменных ![]() .
.
С ней поступают аналогичным образом и так далее.
Заметим,
что ![]()
Второй
случай заменой переменных ![]() сводится
к первому.
сводится
к первому.
Приведение квадратичной формы к диагональному виду. Пусть Q квадратичная форма на линейном пространстве V (над произ- вольным полем, в котором 1 + 1 6= 0). Существует базис, в котором мат- рица квадратичной формы Q диагональна.
