5. Контрольные вопросы

1. Что называют прямыми измерениями?

2. Какие измерения являются многократными?

3. Что обычно принимается за результат измерения?

4. Что такое вариационный ряд?

5. Назовите основные характеристики точечных оценок.

6. Каковы преимущества среднего арифметического перед другими оценками?

7. Что является недостатком среднего арифметического?

8. Что такое дисперсия?

9. Что делать, если дисперсия неизвестна?

ЛАБОРАТОРНАЯ РАБОТА № 2 ПОСТРОЕНИЕ ГИСТОГРАММЫ ПО РЕЗУЛЬТАТАМ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ /на примере результатов математического эксперимента/

1. Цель работы

Цензурирование выборки (исключение промахов).

Освоить основные приемы построения различных гистограмм по результатам многократных измерений, а также элементарной проверки предположения о нормальном законе распределения.

2. Задание

Найти и исключить промахи из выборки.

Построить гистограмму частот или гистограмму статистического распределения. Проверить гипотезу о нормальном законе распределения по ее виду. По имеющейся выборке значений построить доверительный интервал для неизвестного истинного значения.

3. Краткая теория

Поскольку (а следовательно и) чувствительно к промахам, такой результат (промах) подлежит исключению. Таковыми могут оказатьсяи. Вопрос об исключении отдельного результата решается с помощью статистических критериев. Вычислив предварительные оценкии, можно проверитьипо статистике для резко выделяющихся наблюдений:

, (2.1)

или

. (2.2)

Вычисленные по формулам (2.1) или (2.2) значения статистики следует сравнить с критическим (предельным для данной статистики) значениемдля уровня значимости. Если вычисленное значениепревышает, результат признается промахом и отбрасывается. После исключения промаха вычисленияипроизводят заново без учета отброшенного значения.

Построение гистограммы

Для построения гистограммы вариационный ряд разбивают на интервалы одинаковой, произвольной или специальным образом выбранной длины. В простейшем случае интервалы берут одинаковой длины. Вопрос о необходимом числе интервалов для построения гистограммы не имеет строгого решения. Обычно для определения числа интервалов одинаковой длины пользуются формулой Старджеса:

(2.3)

Число результатов отдельных измерений в каждом интерваленазывается частотой попадания вk-й интервал, а относительная частотаназывается в метрологии частностью (мы будем использовать выражение «относительная частота), здесь– общее число измерений. Гистограммойчастот будет являться график в виде прямоугольников, причем по оси абсцисс отложены границы интервалов, а по оси ординат – частоты или относительные частоты (рис. 2.1).Ширина прямоугольников равна длине интервала, а высота – соответствующей частоте или относительной частоте. На гистограмме частот сумма всех высот прямоугольников равна, а на гистограмме относительных частот – единице. Для обоих видов гистограмм все интервалы должны иметь одинаковую длину(называется также шагом гистограммы).

Если по оси ординат отложить величину , то такая гистограмма называется гистограммой статистического распределения, она является выборочной оценкой функции плотности вероятности. Сумма площадей всех прямоугольников на этой гистограмме равна 1. При построении такой гистограммы не обязательно сохранять постоянной длину интервалов.

По любой из этих гистограмм – частот, относительных частот (обе – только с постоянным шагом, иначе возможны значительные искажения формы гистограммы) и статистического распределения – можно составить представление о законе распределения. Удобнее всего это сделать с помощью гистограммы относительных частот. Относительная частота есть оценка вероятности попадания в k-й интервал. Теоретическую вероятностьможно вычислить по формуле:

, (2.4)

где – нижняя и верхняя границыk-го интервала;;– значение интегральной функции стандартного нормального распределения для.

Поскольку при нормальном распределении случайная величина может принимать значения на интервале от до, а в реальном случае интервал конечный (,), сумма всех вероятностейпо всемrинтервалам будет меньше единицы. Проверку правильности вычислений можно осуществить следующими способами:

• вычислить вероятности попадания случайной величины во внешние интервалы (,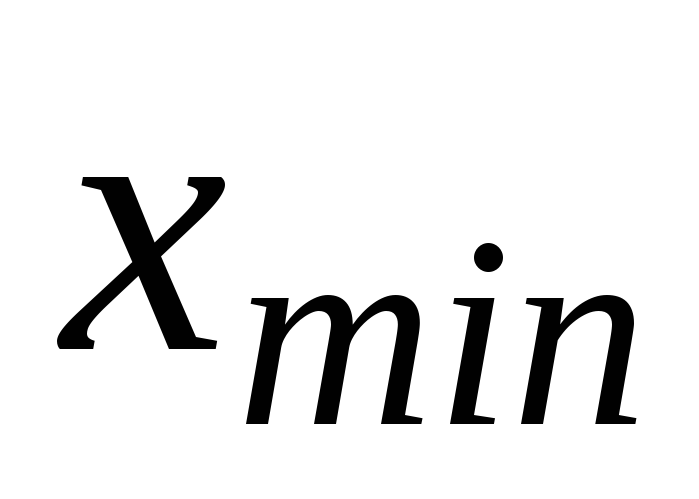) и (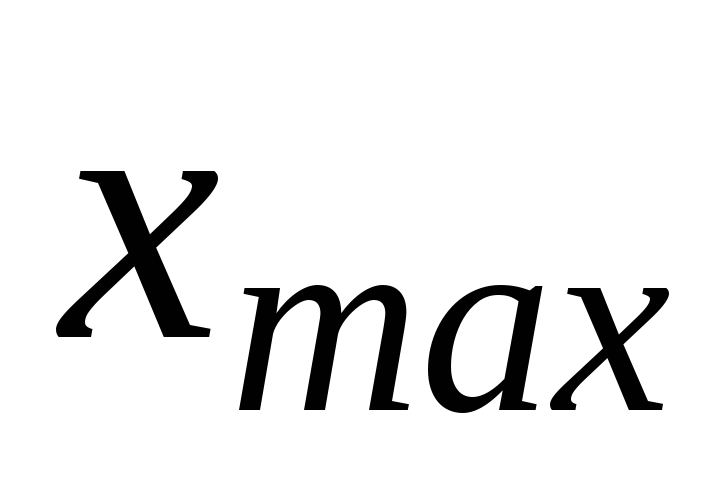,) и прибавить полученные значения к сумме вероятностей по всемr интервалам (в результате должна получиться 1);

• вычислить вероятность попадания случайной величины в интервал (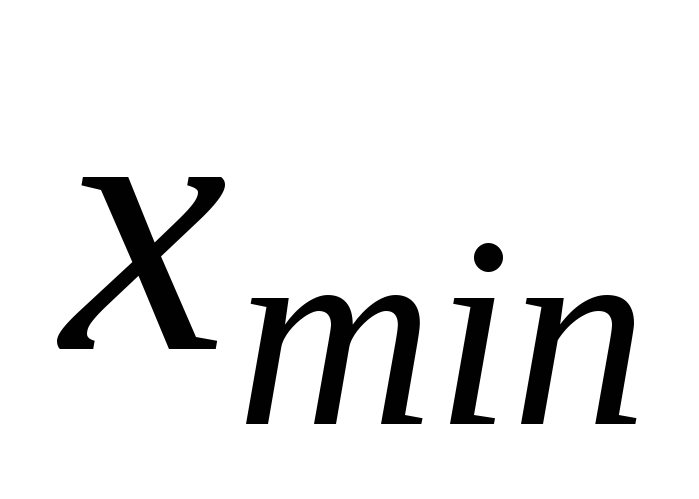,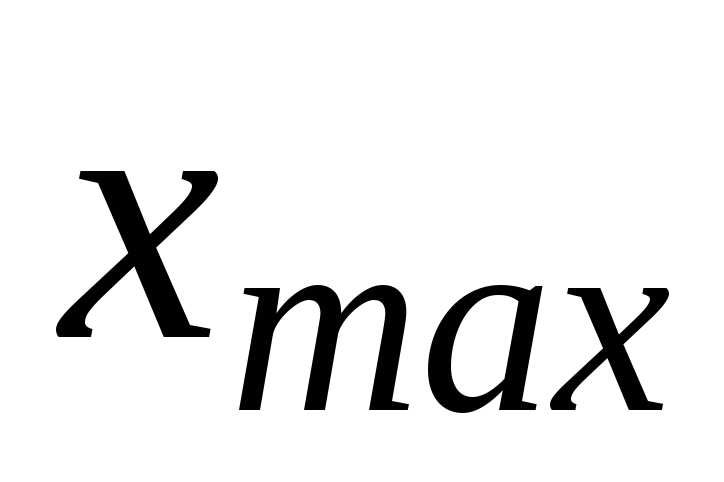) – эта вероятность должна быть равна сумме вероятностей по всемrинтервалам.

Краткие технические сведения о построении различных диаграмм и графиков средствами Excelможно найти в прил. 3 «Теория диаграмм».

Доверительным называется интервал значений, который в последующих опытах накрывает неизвестное истинное значение с вероятностью равной заданной [4, 5].

Для построения доверительного интервала для математического ожидания (истинного значенияпри центрированных ошибках) воспользуемся соотношением, называемым дробью Стьюдента, которое имеетt-распределение:

, (2.5)

Пользуясь таблицами t-распределения, можно построить доверительный интервал для истинного значения:

(2.6)

где – критическое значениеt-распределения при уровне значимостии числе степеней свободы (числе независимых слагаемых в (1.9) и (2.5)).

Интервал в метрологии называется доверительной случайной погрешностью. Доверительным интервалом по выражению (2.6) пользуются, когда ошибки измерений имеют нормальное распределение. В данной работе предлагается визуально по гистограмме проверить гипотезу о нормальности распределения случайной величины.

Полуширину доверительного интервала можно рассчитать так:

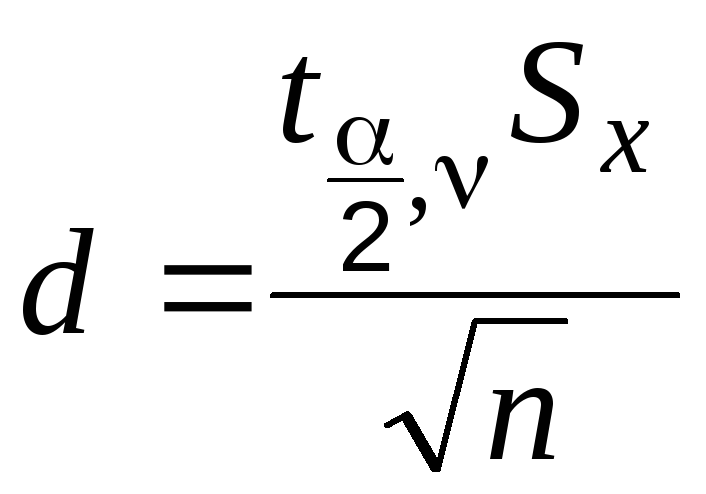, (2.7)

где значения инужно определить по выборке (лаб. работа «Первичная обработка…»).

Следует при этом иметь в виду, что использование терминов «вероятность» и «доверительная вероятность» применительно к конкретному интервалу , построенному по данной выборке некорректно. Этот интервал может в действительности накрыть неизвестное истинное значение (и тогда следовало бы сказать, что вероятность равна единице), либо не накрыть его (тогда следовало бы сказать, что вероятность равна нулю). Это остается неизвестным исследователю. Однако, еслидостаточно мало, можно ожидать, чтоскорее всего накрытие имеет место, то есть доля «накрывающих» интервалов, равная , гораздо больше, чем доля противоположных, равная). Чтобы отразить нашу уверенность, что скорее всего построенный нами интервал относится к «накрывающим», используется термин «надежность». Надежность численно равна доверительной вероятности:

.