МатМод экология / Лекция №3

Лекция №3.

Построение аналитической модели по данным экспериментов.

Моделирование на стадии эксперимента происходит при попытке выявления зависимостей результата от наиболее существенных факторов.

Это позволяет обобщить результат экспериментирования в виде некоторой математической формулы, т.е. аналитической модели.

Например, для свободно падающих тел Галилеем был установлен факт независимости скорости свободного падения тел в вакууме вблизи поверхности земли от их массы, плотности, размеров. Это обстоятельство может быть проверено путем измерения зависимости скорости свободного падения от времени для контрольной группы тел. Если нанести результаты измерений на график V(t) , то через совокупность экспериментальных точек с учетом погрешностей измерений для каждого тела легко может быть проведена прямая (см. рис. 3.1),

Рис. 3.1. Зависимость V от t

что позволяет выполнить аппроксимацию по формуле (уравнение

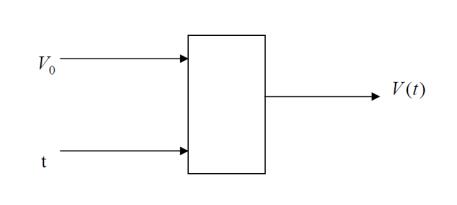
С помощью статистической обработки с некоторой погрешностью может быть найден тангенс угла наклона данной прямой, то есть величина g ,

являющаяся по смыслу ускорением свободного падения. Сопоставление величины ускорения для разных тел позволяет повторить вывод Галилея.

Таким образом, мы устанавливаем некоторый “закон”, выражаемый математической моделью (формулой) (3.1).

Заметим принципиальный момент: нам так и осталась непонятной природа этого явления, но, имея формулу (3.1), мы обладаем инструментом прогнозирования. Здесь мы сталкиваемся c широко известной информационной технологией “черного ящика”, получившей широкое распространение в кибернетике. “Черный ящик”, соответствующий формуле

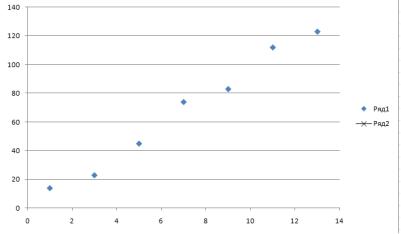
(3.1), схематично можно изобразить так, как это показано на рис. 3.2.

Рис. 3.2. Модель “черный ящик” Этим способом удаѐтся установить также и довольно сложные

зависимости, например степенные. Так, по экспериментальным данным Шарлем Кулоном в 1785 был открыт закон Кулона. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.

Так исторически возникало большинство физических законов. Закон – это на самом деле результат абсолютизации математической зависимости,

найдя которую редко удается понять природу явления. Абсолютизация, как показывает исторический опыт, никогда не является достаточно правомерной.

Например, достоверно известно, что закон Кулона справедлив вплоть до атомных размеров, но нарушается на расстояниях, сопоставимых с межнуклонными размерами внутри атомного ядра (т.е. 10 –14м).

Таким образом, все известные естественнонаучные законы на самом деле всего лишь аналитические модели реальных явлений.

Аппроксимация экспериментальных данных.

Пусть проведено некоторое количество экспериментов, в результате которых для каждого заданного начального значения исходных данных получен численный ответ системы (например, проведено 10 экспериментов по бросанию тел с разной высоты, измерено время падения и скорость в момент падения). В результате получится таблица, описывающая неизвестную пока аналитическую модель (функцию):

Всегда следует помнить, что измерения проводятся с некоторой погрешностью.

Под аппроксимацией будем понимать описание таблично заданной функции некоторой математической зависимостью – аналитической моделью.

Исходными данными для решения задачи является таблица наблюдений

– набор значений независимых переменных и соответствующие им значения

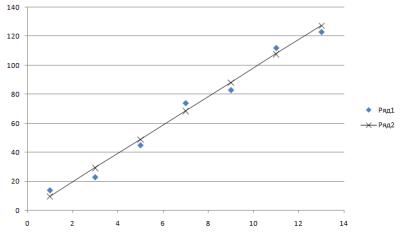
Рис. 3.2.

После того, как выбран общий вид функции, необходимо лишь рассчитать наилучшие значения коэффициентов этого уравнения. Очевидно,

что коэффициенты уравнения следует подбирать так, чтобы рассчитываемые по уравнению значения функции отклика максимально близко совпадали с заданными в исходной таблице наблюдений.

Так, для нашего примера: уравнение прямой имеет общий вид: f(x)=a1+a2*x

Следовательно, необходимо определить значения коэффициентов a1 и a2.

Определение коэффициентов аналитической модели по методу наименьших квадратов (МНК).

Пусть между величинами x и y существует функциональная

зависимость, заданная таблицей пар значений:

ставится задача полного равенства значений функции и экспериментальных данных в точках xi, а лишь минимального отличия их значений.

Если в эмпирическую формулу (3.3) подставить исходные точки xi , то получим теоретические значения:

найденной эмпирической функции от заданных значений функции будет минимальной.

равенство нулю градиента функции (вектора частных производных). В

результате получим систему уравнений для определения коэффициентов

Таким образом, нахождение коэффициентов ai сводится к решению системы (3.6). Конкретный вид системы зависит от выбранного вида аппроксимирующей функции f (x;a1 ,a2 ,...,am ) .

Так, если эмпирическая формула (3.3) линейна относительно

Эта линейная система может быть решена любым известным методом

(методом Гаусса, простых итераций, формулами Крамера и др.).

В случае квадратичной зависимости:

Методом наименьших квадратов удается рассчитать коэффициенты и более сложных аппроксимирующих функций, однако для этого приходится применять дополнительные преобразования. Так, например, МНК применяется для расчета коэффициентов экспоненциальной функции:

экспоненциальной функции в линейную относительно коэффициентов a1 и a2

-линеаризации. Линеаризация достигается путем логарифмирования равенства (3.8), после чего получаем соотношение

Построенная на основе выбранной эмпирической функции модель также называется моделью регрессии, а вычисленные по методу МНК коэффициенты – коэффициентами регрессии.

Оценка адекватности построенной аналитической модели.

После того, как аналитическая модель построена (определены коэффициенты выбранной эмпирической функции) необходимо оценить,

насколько точно выбранная модель отражает реальную зависимость y от x.

Для проверки согласия построенной модели регрессии с результатами эксперимента обычно вычисляют следующие числовые характеристики:

среднеквадратическая ошибка, коэффициент корреляции (линейная

зависимость), и коэффициент детерминации.

Среднеквадратическая ошибка напрямую показывает суммарное отклонение экспериментальных и теоретически предсказанных данных, и

определяется так же, как и в методе наименьших квадратов:

рассчитанные при помощи построенной по МНК функции. Чем меньше значение ошибки Е, тем лучше функция описывает эксперимент. Однако такая оценка адекватности модели не всегда объективна, так как функция может хорошо отражать значения в узлах xi, но плохо отражать общую закономерность процесса:

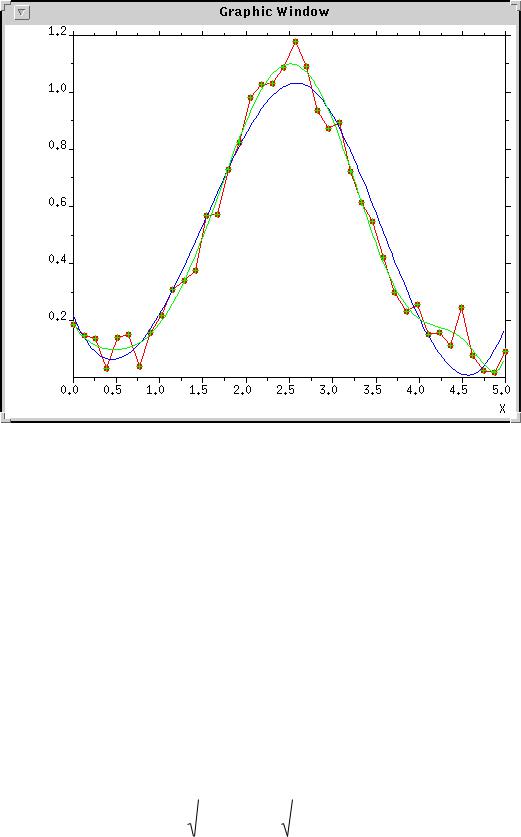
Рис.3.1.

Функция, нарисованная красным, даст практически нулевую квадратичную ошибку, но синий график гораздо лучше отражает процесс.

Коэффициент корреляции - более объективная оценка адекватности,

однако применять ее целесообразно лишь для линейных моделей. Он является мерой линейной связи между переменными и показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой.

Коэффициент корреляции вычисляется по формуле:

значений x и y.

Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе к 1, тем теснее

линейная связь между x и y.

Чтобы выяснить, насколько точно построенная модель отражает эмпирические данные нелинейной системы (в общем случае - произвольной),

вводится еще одна характеристика коэффициент детерминации. Он показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными

системы.

Для его описания рассмотрим следующие величины:

квадратов. Оно характеризует отклонение экспериментальных данных от теоретических.

суммой квадратов. Оно характеризует разброс теоретических данных вокруг среднего значения.