МатМод экология / Лекция №9

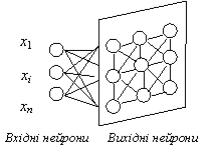
Лекция №9

Сеть Кохонена.

Сеть разработана Тойво Кохоненом в начале 1980-х гг. и принципиально отличается от рассмотренных выше сетей, поскольку использует неконтролируемое обучение (обучение без учителя) и обучающее множество состоит лишь из значений входных переменных.

Сеть распознает кластеры в обучающих данных и распределяет данные по соответствующим кластерам. Если дальше сеть встречается с набором данных, непохожим ни на один из известных образцов, она относит его к нового кластеру. Если в данных содержатся метки классов, то сеть способна решать задачи классификации.

Сеть Кохонена имеет всего два слоя: входной и выходной, ее называют самоорганизованной картой. Элементы карты располагаются в некотором пространстве - как правило, двумерном.

Рис. 9.1. Сеть Кохонена

Сеть Кохонена учится методом последовательных приближений.

Начиная со случайным образом выбранного выходного расположения центров, алгоритм постепенно улучшается для кластеризации обучающих данных.

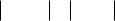
Основной итерационный алгоритм Кохонена последовательно проходит ряд эпох, на каждой эпохе обрабатывается один обучающий пример.

Входные сигналы (векторы действительных чисел) последовательно предъявляются сети, желаемые выходные сигналы не определяются. После предъявления достаточного числа входных векторов, синоптические веса сети определяют кластеры. Веса организуются так, что топологически близкие узлы чувствительны к похожим входным сигналам.

Основой алгоритма обучения сети Кохонена является правило

«победитель получает все». Для каждого входного вектора определяется свой нейрон-победитель (с индексом i*). Он будет служить прототипом этого вектора. Поэтому победитель выбирается так, что его вектор весов wi* ,

определенный в том же d-мерном пространстве, находится ближе к данному входному вектору, чем у всех остальных нейронов: wi* x wi x для всех i.

Выход такого нейрона усиливается до единичного, а остальных - подавляется до нуля.

Количество нейронов в соревновательном слое определяет максимальное разнообразие выходов и выбирается в соответствии с требуемой степенью детализации входной информации. Обученная сеть может затем классифицировать входы: нейрон-победитель определяет, к

какому классу относится данный входной вектор.

Алгоритм обучения соревновательного слоя нейронов

Алгоритм обучения соревновательного слоя состоит в изменении весов нейронов по правилу:

поскольку задача сети - как можно точнее отразить входную информацию в выходах сети. В соревновательном слое лишь один нейрон-

победитель имеет ненулевой (единичный) выход. Соответственно, в согласии с выписанным выше правилом, лишь его веса корректируются по предъявлении данного примера, причем для победителя правило обучения имеет вид:

Описанный алгоритм обучения на практике обычно несколько модифицируют, т. к. он, например, допускает существование т. н. мертвых нейронов, которые никогда не выигрывают, и, следовательно, бесполезны.

Самый простой способ избежать их появления - выбирать в качестве начальных значений весов случайно выбранные в обучающей выборке входные вектора.

Модифицированное Кохоненом правило соревновательного обучения

учитывает расстояние нейронов от нейрона-победителя |i-j| :

Для реализации алгоритма необходимо определить меру соседства нейронов (окрестность нейрона-победителя). На рис. 9.2 показаны зоны топологического соседства нейронов на карте признаков в разные моменты времени. NEj(t) - множество нейронов, считающиеся соседями нейрона j в

момент времени t. Зоны соседства уменьшаются с течением времени.

Рис. 9.2. Зоны топологического соседства на карте признаков в разные моменты

времени

Функция соседства (|-i*|) равна единице для нейрона-победителя с индексом i* и постепенно спадает с расстоянием, например по закону:

Как темп обучения η, так и радиус взаимодействия нейронов постепенно уменьшаются в процессе обучения, так что на конечной стадии обучения мы возвращаемся к базовому правилу адаптации весов только нейронов-победителей.

В результате такого обучения мы получаем не только квантование входов, но и упорядочивание входной информации в виде одноили двумерной карты. Каждый многомерный вектор имеет свою координату на этой сетке, причем чем ближе координаты двух векторов на карте, тем ближе они и в исходном пространстве. Такая топографическая карта дает наглядное представление о структуре данных в многомерном входном пространстве,

геометрию которого мы не в состоянии представить себе иным способом.

Визуализация многомерной информации является главным применением карт Кохонена.

Удобным инструментом визуализации данных является раскраска топографических карт, аналогично тому, как это делают на обычных географических картах. Каждый признак данных порождает свою раскраску ячеек карты - по величине среднего значения этого признака у данных,

Алгоритм функционирования сети Кохонена

1.Инициализация сети. Весовым коэффициентам сети даются небольшие случайные значения. Общее число синоптических весов - M*N (см.

Рис. ). Начальная зона соседства показана на Рис. .

2.Предъявление сети нового входного сигнала.

3.Вычисление расстояния до всех нейронов сети:

Расстояния dj от входного сигнала до каждого нейрона j

определяются по формуле:

где xi - i-ый элемент входного сигнала в момент времени t, wij(t) -

вес связи от i-го элемента входного сигнала к нейрону j в момент времени t.

4.Выбор нейрона с наименьшим расстоянием: выбирается нейрон-

победитель j*, для которого расстояние dj самое малое.

5.Настраивание весов нейрона j* и его соседей:

Делается настраивание весов для нейрона j* и всех нейронов из его окрестности NE. Новые значения весов:

где η(t) - скорость обучения, которая уменьшается с течением времени (положительное число, меньше единицы).

6.Возвращение к шагу 2.

Валгоритме используется коэффициент скорости обучения, который постепенно уменьшается, для тонкой коррекции на новой эпохе. В результате центр устанавливается в определенной позиции, которая удовлетворительным образом кластеризует примеры, для которых данный нейрон является победителем.

После того, как сеть научена распознаванию структуры данных, ее

можно использовать как средство визуализации при анализе данных.

Задача, решаемая данной сетью, как правило, формулируется так.

Известен некоторый образцовый набор двоичных сигналов (изображений,

звуковых оцифровок, других данных, которые описывают определенные объекты или характеристики процессов). Сеть должна уметь с зашумленного сигнала, представленного на ее вход, выделить ("припомнить" по частичной информации) соответствующий образец или "дать вывод" о том, что входные данные не отвечают ни одному из образцов.

Сеть Хопфилда представляет собой ассоциативную память. «Ассоциативная память» означает, что по вектору, поданному на вход,

сетью будет создан на выходе один из запомненных ранее эталонных векторов, наиболее "похожий" (в некотором выбранном смысле) на данный входной вектор. Пусть компоненты эталонных векторов могут принимать только значения +1 и -1.

Ответ сети Хопфидла для i-того нейрона для каждого следующего (t+1)

цикла может быть представлен выражением:

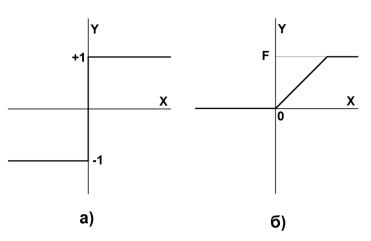
где f - передаточная функция в виде пороговой, приведена на рис. 9.4.

Рис. 9.4. Передаточные функции

по заданному набору эталонных образов. Именно этой матрицей весовых коэффициентов набор эталонов и запоминается в сети.

Алгоритм функционирования сети

1.На стадии инициализации сети синаптические коэффициенты устанавливаются таким образом:

Здесь i и j - индексы, соответственно, предсинаптического и постсинаптического нейронов; xik, xjk - i-ый и j-ый элементы вектора k-

ого образца.

2.На входы сети подается неизвестный сигнал. Его распространение непосредственно устанавливает значения выходов:

yi(0) = xi , i = 1...n,

поэтому обозначения на схеме сети входных сигналов в явном виде носит чисто условный характер. Ноль в скобке yi означает нулевую итерацию в цикле работы сети.

3. Рассчитывается новое состояние нейронов

n

S(t 1) wij yj (t), j 1,n (9.12)

i 1

и новые значения выходов

4.Проверяем, изменились ли выходные значения выходов за последнюю итерацию. Если да - переход к пункту 2, иначе (если выходы стабилизировались) - конец. При этом выходной вектор представляет собой образец, что лучше всего отвечает входным данным.

Иногда сеть не может провести распознавания и выдает на выходе

несуществующий образ. Такой образ часто называют «химерой». Это связано

с проблемой ограниченности возможностей сети. Для сети Хопфилда число запомненных образов m не должно превышать величины, приблизительно равной 0.15*n (15% от размерности векторов).

Вероятностная нейронная сеть.

Вероятностная нейронная сеть применяется для решения задач классификации. В отличие от задач кластеризации, где классы, на которые необходимо разбить множество данных, не заданы, в задаче классификации указано количество классов, к которому может быть отнесен каждый пример,

и задано обучающее множество – для каждого обучающего набора определн класс. к которому он относится.

Вероятностная сеть для каждого входного вектора определяет вероятности, с которыми этот вектор принадлежит каждому классу.

Вероятностная сеть имеет три слоя: входной, радиальный и выходной.

Радиальный нейрон – это нейрон, функцией активации которого является Гауссиан, соответствующий выражению для плотности вероятности при нормальном распределении:

Выражение записано для j-того нейрона. Здесь mi – n-мерный центр функции (аналог математического ожидания), а - разброс (аналог дисперсии). Для двумерного входного вектора (x1,x2) радиальная функция активации имеет вид: