Вафля контрольные 1 часть

1. Параметрические уравнения материальной точки массой т можно представить в полиномиальной форме: . Определить параметры этих уравнений, если при t = 0: х = х₀; у = у₀; v_x = v_хо v_у = v_y0; F_x = F_xo; F_y = F_y0. Построить графики изменения координат точки в зависимости от времени, а также график траектории движения за период времени до t₂. Для момента времени t₁ найти векторы скорости, ускорения, силы, а также радиус кривизны траектории. Под каким углом к горизонту направлена начальная скорость материальной точки?

Дано: m = 8 г = 0,008 кг; x₀ = 8 м; v_x0 = 18 м/с; F_x0 = - 6.4 мН; y₀ = 8 м; v_y0 = 18 м/с;

F_y0 = - 81 мН; t₁ = 4 c; t₂ = 6 c.

Проекции скорости точки на оси координат

Проекции ускорения точки

Согласно второму закону Ньютона проекции силы на оси координат

При t = 0 имеем откуда м м.

откуда м/с м.

Откуда м/с²; м/с²

Уравнения движения примут вид (1)

;

При t =t₁ = 4 c имеем x = 67.2 м; y = - 82 м;

v_x = 11.6 м/с; v_y = - 63 м/с; ;

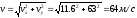
Касательное ускорение найдем путем дифференцирования модуля скорости м/с²

Нормальное ускорение м/с²

Радиус кривизны траектории м

По уравнениям (1) составляем таблицу и строим графики.

t с	0	0,5	1	1,5	2	2,5	3	3,5	4	4,5	5	5,5	6
x м	8	16,8	25,2	33,2	40,8	48	54,8	61,2	67,2	72,8	78	82,8	87,2
y м	8	14,5	15,9	12,2	3,5	-10,3	-29,1	-53	-82	-116	-155,1	-199,3	-248,5

2. В установке, показанной на рисунке известны диаметр D однородного сплошного цилиндра из материала Ме и его толщина b массы тел m₁, m₂. Найти угловое ускорение цилиндра и отношение сил натяжений T₁/T₂ вертикальных участков нити в процессе движения, если опора подвеса движется с ускорением а₀ вверх.

Дано; D = 8 см; b = 18 мм; m₁ = 8 кг; m₂ = 6 кг; a₀ =2 м/с²; Ме = Cu; кг/м³.

рассмотрим относительное движение грузов относительно подвижной систему координат движущейся вместе с подвесом

Запишем в векторной форме уравнение поступательного движения грузов и вращательного движения цилиндра

где М₁ и М₂ моменты от сил натяжения нитей Т₁ и Т₂ соответственно. Спроецируем первые два на ось х а третье на ось у и добавим уравнение кинематической связи получим систему 4 уравнений m₁a = m₁g + m₁a₀ – T₁ (1);

– m₂a = m₂g + m₂a₀ – T₂ (2)

J = RT₁ – RT₂ (3); a = R (4)

подставляя (4) в (3) с учетом J = mR²/2 прилучим

ma/2 = T₁ – T₂ (5)

Вычитая (2) из (1) и подставив в (5) получим (6)где

m =V =R²b = кг; м/с²

Угловое ускорение цилиндра из (4) рад/с

Полное ускорение грузов а₁ = а – а₀ = – 0,36 м/с²; а₂= – а – а₀ = – 3.64 м/с²

Знак минус показывает что ускорения направлены в сторону противоположную показанной на рисунке.

Подставляя в (1) и (2) с учетом направлений получим

Т₁ = m₁(g – a + a₀) = 8(9,8 – 1.64 + 2 )= 81,3 Н;

Т₂ = m₂(g + a + a₀) = 6(9,8 +1.64 + 2)= 80,6Н;

3. На железнодорожной платформе, движущейся со скоростью V, закреплено орудие, ствол которого направлен в сторону движения под углом α к горизонту. Орудие произвело выстрел, после чего скорость платформы уменьшилась в n раз. Найти на какое расстояние улетит снаряд, если его масса m, а масса платформы с орудием М.

Дано: V = 18 км/ч = 5 м/с; α = 45^o; n = 1,08; m = 80 кг; M = 80 т = 80000 кг

Скорость платформы после выстрела V₁ = V/n = 4,63 м/с

По закону сохранения импульса в проекции на направление движения

MV = MV₁ + mUcosα Отсюда м/с.

запишем уравнения движения снаряда, происходящего под действием силы тяжести в проекциях на оси координат

В момент падения снаряда t = τ Откуда время полета снаряда с. Тогда дальность полета снаряда м ≈ 19,7 км

4. Два груза из свинца с радиусами r₁ и г₂ подвешены на нитях длиною l так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол φ и выпущен. На какую высоту поднимутся грузы после абсолютно неупругого удара? На сколько повысится их температура?

Дано: r₁ = 8 см; r₂ = 4 см; l = 2 м; φ = 40^о

Массы шариков кг кг

Отклоненный груз обладает потенциальной энергией

W_П =m₁gh = m₁g(l - lcos)= 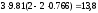Дж

При отпускании шарика потенциальная энергия переходит в кинетическую

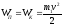откуда м/с

По закону сохранения импульса при неупругом ударе Откуда м/с из соотношения найдем высоту подъема шариков м

По закону сохранения энергии Дж

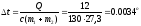
5. В двух баллонах с объемами V₁ и V₂ содержатся газы G₁, G₂ при температуре T, плотности которых, соответственно р₁ и р₂ Найти давления в баллонах, концентрации и общее количество молекул каждого газа. Какое давление установится, если баллоны соединить вместе, а температура при этом не измениться? Определить эффективную молярную массу смеси и ее плотность

Дано: V₁ = 8 л; V₂ = 12 л; G₁ = He; G₂ = C₃H₈; ρ₁ = 0.8 кг/м³; ρ₂= 8 кг/м³; t = 8^oC.

Определим массы газов в баллонах кг кг

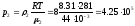Из уравнения Менделеева – Клапейрона находим Па Па

Количество молекул газа

Согласно закона Дальтона где Па Па и Па

Эффективная молярная масса смеси кг/моль

Плотность смеси кг/м³.

6. Газ G массой т имеет температуру T и давление р₁. Чему равняется энергия поступательного и вращательного движения молекул этого газа? Какая теплота сообщается газу, если при постоянной температуре давление уменьшается до р₂ Найти работу, совершенную при расширении, среднеарифметическую и среднеквадратичную скорости молекул. Вычислить долю молекул, скорости которых лежат в диапазоне от v₁ = 380 м/с до v₂ = 480 м/с

Дано: G = H₂; m = 8 г; p₁ = 8 ат = 8,1^.10⁵ Па; t = 8^оС; p₂ = 2 ат =2,02^.10⁵ Па; v₁ = 380 м/с; v₂ = 480 м/с

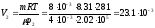Из уравнения Менделеева – Клапейрона объем занимаемый газом до расширения м³. и после м³

Согласно первому началу термодинамики

Изменение внутренней энергии так как

Работа изотермического расширения Дж

Кинетическая энергия молекул

Энергия поступательного движения 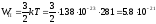Дж

Энергия вращательного движения Дж

Среднеарифметическая скорость молекул м/с

Среднеквадратичная скорость молекул м/с

Наиболее вероятная скорость м/с м/с.

Так как интервал скоростей велик, нельзя использовать формулу Максвелла

Найдем число молекул скорости которых больше v₁ и v₂ Тогда скорости лежащие в интервале от v₁ до v₂ N_x = N₁ – N₂ Значения N₁ N₂ найдем по графику зависимости N_x/N от u Тогда

функция распределения Максвелла

вычисляем тогда искомая доля молекул

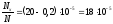
Строим графики

v	100	300	380	480	500	700	900	1100	1300	1500	1700	1900
u	0,093	0,278	0,352	0,444	0,463	0,648	0,833	1,018	1,203	1,388	1,573	1,758
u2	0,009	0,077	0,124	0,197	0,214	0,420	0,694	1,036	1,448	1,927	2,475	3,092
exp-u2	0,991	0,926	0,884	0,821	0,807	0,657	0,500	0,355	0,235	0,146	0,084	0,045
f(v)	1,64201E-06	4,14E-05	8,03E-05	0,0002	0,0002	0,0004	0,0006	0,0008	0,0009	0,0008	0,0007	0,0005

7. Идеальная тепловая машина, работающая по циклу Карно, температуру нагревателя t_н и температуру холодильника t_х. Во сколько раз нужно увеличить температуру нагревателя, чтобы КПД машины увеличился в п раз? Вычислить работу расширения и изменение энтропии газа при этом, если рабочим телом является газ G массой m расширяется от давления р₁ до давления p₂

Дано: Т_н = 328^оС = 601^оК; Т_х = 238^оС = 511^оК;n = 1.8; G = Ar; m = 8 г = 0,014 кг;

р₁ = 48 ат = Па ; р₂ = 8 ат = Па. кг/моль

КПД цикла Карно тогда и Следовательно раза

Первоначальный объем газа из уравнения Менделеева – Клапейрона 3605628

Из уравнения адиабаты 4-1

Откуда

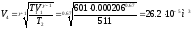
Кроме того откуда

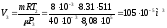
Из уравнения адиабаты 2-3

Откуда

Кроме того откуда

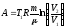
Работа при изотермическом процессе Тогда

изменение энтропии

8. Два точечных заряда расположены на вершинах А и С квадрата АВСD Причем q₂ = nq₁. Заряды взаимодействуют между собой с силой F. Определить напряженность электростатического поля и потенциал в точке В. Построить графики изменения напряженности и потенциала поля вдоль оси x направленной по диагонали квадрата. Напряженность считать положительной, если ее направление совпадает с направлением оси x

Дано: АВ = 8 см; n = 3; F = 8 мкН

Cила взаимодействия двух точечных зарядов 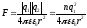где 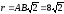см Откуда Кл

Кл

Напряженность поля точечного заряда

Найдем напряженность поля в точке В

От заряда q₁ 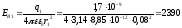В/м

От заряда q₂ В/м

Так как Е_В1 и Е_В2 взаимно перпендикулярны то

В/м

Потенциал поля точечного заряда

Тогда В В и В

В виду симметричности относительно оси x В/м В

На оси x направленной по диагонали квадрата направление напряженностей вдоль оси x поэтому

и

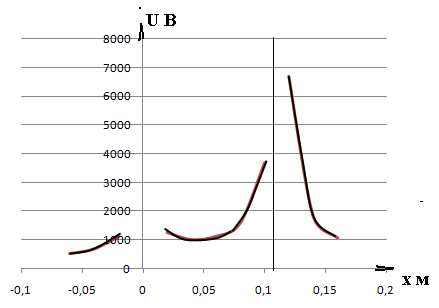
Составляем таблицу и строим графики

x м	-0,06	-0,04	-0,02	0,02	0,04	0,06	0,08	0,1	0,12	0,14	0,16
Е В/м	-5784	-11523	-40845	32943	949	-12090	-39758	-270068	937797	63744	21376
U B	520	683	1110	1259	1011	1121	1582	3684	6685	1809	1072

9. Кольцо радиуса r из тонкой проволоки имеет заряд q . Найти модуль напряженности и потенциал электрического поля на оси кольца как функцию расстояния х до его центра. (Использовать принцип суперпозиции полей). Определить максимальное значение напряженности и соответствующее расстояние х_тах . Построить графики Е = Е(х), φ =φ{х).

Дано r = 8 см; q = 4 нКл

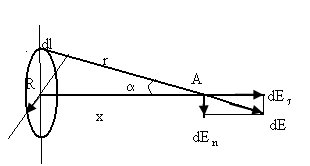
Возьмем элемент кольца dl имеющий заряд dq. Напряженность поля создаваемая этим элементом в точке А вектор dЕ направлен по линии соединяющей элемент dl с точкой А. Для нахождения напряженности от всего кольца нужно сложить dE от всех элементов Разложим вектор dE на составляющие dE_n и dE_τ составляющие dE_n от двух диаметрально расположенных элементов взаимно уничтожаются. Тогда Е = ∫dE_τ

Но Учитывая что получим (1) - напряженность на оси кольца.

Аналогично для потенциала поля

(2)

Выразим x и r через угол α R = rsinα; x = rcosα тогда

Для нахождения максимума напряженности возьмем производную dE/dα и приравняем ее нулю или tq²α = 2. Тогда напряженность электрического поля имеет максимальное значение в точке А расположенной на расстоянии см

По формулам (1) и (2) строим графики

x	0	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,1	0,11	0,12	0,13	0,14
E	0	687	1283	1731	2012	2143	2159	2097	1988	1855	1713	1573	1440	1315	1202
U	450	446	436	421	402	381	360	339	318	299	281	265	250	236	223

10. Диэлектрический шар с диэлектрической проницаемостью ε, радиусом R_o равномерно заряжен с объемной плотностью ρ и окружен концентрическим слоем проводника радиуса R. Определить поверхностные плотности зарядов на поверхностях проводника. Построить графики зависимостей напряженности поля - Е = Е(r), электрического смещения - D = D(r) и потенциала - φ = φ (r).

Дано: R₀ = 6 см; R = 12 см; ε = 8; ρ = 8 мкКл/м³

Согласно теореме Остроградского-Гаусса напряженность поля внутри заряженной сферы

(1)

потенциал поля (2)

Электрическое смещение (3)

В слое проводника Е = 0; ; и D = 0.

При R > R Напряженность поля (4)

Потенциал поля (5)

Электрическое смещение (6)

Из условия, что в зоне проводника при r = R₀ имеем Кл/м².

Из условия вне зоны проводника при r = R имеем

Кл/м²

По уравнениям (1) – (6) строим графики

r м	0	0,02	0,04	0,06	0,06	0,08	0,1	0,12	0,12	0,14	0,16	0,18	0,2
Е В/м	0	753	1507	2260	0	0	0	0	4520	3321	2542	2009	1627
D мкКл/м2	0,000	0,053	0,107	0,160	0,000	0,000	0,000	0,000	0,040	0,029	0,023	0,018	0,014
U B	339	331	309	271	271	271	271	271	271	232	203	181	163