
ГидравликаВиВ
.pdf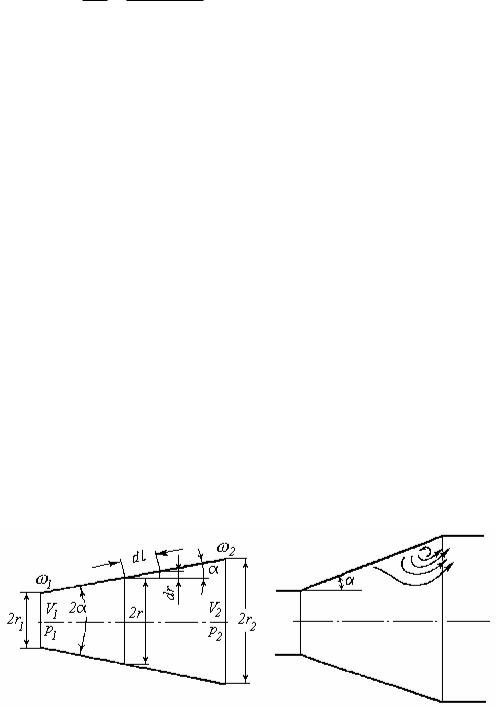
p V |
2 |
|
p |
2 |
V |
2 |
|
(V V |
2 |
) |
2 |
|
|
|||
1 |
|
1 |
|
|
|
|
2 |
|
|
1 |
|
|
. |
(5.6) |
||
g |
|
|
g |
|
|
2g |
|
|
|
|||||||
|
2g |
|
2g |
|
|
|
|
|
||||||||
Запишем уравнение Бернулли для сечений 1−1 и 2−2, считая режим турбулентным (α = 1) и учитывая только местные потери (z1 = z2 ):
p |
V |
2 |
|
p |
2 |
|
V 2 |
|
V |
2 |
|
|
|
1 |
|
1 |
|
|
|
|
2 |
вр |
1 |
|
. |
(5.7) |
|
|
|
|
|
|
2g |
|
|
||||||
g |
2g |
g |
|
2g |
|
||||||||
Сравнив (5.6) и (5.7), получим:
вр V12 (V1 V2)2 .
2g 2g
Отсюда:
|
(V1 V2) |
2 |
|
|
V2 |
2 |
|
|
V2 |
2 |
|
|
1 |
2 |
|
|||
вр |
|
|
|
V1 |
|
|
|
|
|
|
|
(5.8) |
||||||
|
|
|
V |
V |
|
|||||||||||||
V |
2 |
|
|
|
1 |
|
1 |
|
2 |
. |
||||||||
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим n 2 / 1 (степень расширения). Окончательно получим:
|
|
1 |
2 |
|
||
вр |
1 |
|
|
. |
(5.9) |
|
n |
||||||
|
|
|
|
|
||
В частном случае (если жидкость выходит из трубопровода в бак) можно считать, что n , 1/ n 0, вр 1.
5.2.2. Гидравлические потери в диффузоре
Диффузором называется участок трубопровода конической формы, по которому поток жидкости двигается от меньшего сечения к большему
(рис. 5.4).
Рассмотрим одномерное установившееся движение жидкости от сечения 1 к сечению 2 (рис. 5.4, а). Режим течения − турбулентный, в автомодельной зоне. Гидравлические потери будут складываться из путевых и местных:
hдиф hп hм.
Рис.5.4. Течение жидкости по диффузору
Рассмотрим вначале путевые потери на элементарном участке длины dl, имеющем текущий диаметр 2r (коэффициент считаем постоянным):
dh |
dl |
|
V 2 |
. |
|
(5.10) |
|||||||||
|
|
|
|
||||||||||||
|
п |
|
|
2r |
|
|
2g |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
r |
|
2 |
|
|
|
|
|
|
|
|
|
|
||
Учтем, что V V |
|
1 |
|
|
, так как площади относятся как квадраты радиусов. |
||||||||||
|
|
|
|||||||||||||
1 r |
|
|
|
|
|
|
|
|
|
|
|
||||
Кроме тогоdl dr /sin . Подставим эти выражения в (5.10). |
|||||||||||||||
|
|
|
|
|
dr |
|
|
r |
4 |
V 2 |
|||||
dh |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
. |
||
|
|
|
|
|
|
|
|
||||||||
п |
|
|
2rsin r |
|
2g |
||||||||||
|
|
|
|
||||||||||||
Интегрируя это выражение в пределах от r1 до r2 , получим:
|
r2 |
|
|
dr |
|
V 2 |
|
r |
4 |
|
|
r 4V |
2 r2 |
dr |
|
r 4V 2 |
|
|
|
r 4 |
|
r2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
hп |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2rsin |
|
2g |
|
|
|
|
|
|
|
|
|
|
r |
5 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||||||||
|
r |
|
|
|
|
r |
|
|
2sin 2g r |
|
|
|
|
2sin 2g |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
||
|
|
r14 r2 4 r1 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
V1 |
|
|
r14 |
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
8sin |
2g |
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8sin |
|
r 4 |
|
|
|
|
|
r |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
V1 |
|
||||||||||||
|
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
8sin |
|
|
|
2g |
|
8sin |
|
2g |
|
8sin |
|
|
|
2g . |
|||||||||||||||||||||||||||||||||||||
|
1 |
r |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
1 |
2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь n − степень расширения диффузора.
Местные потери в диффузоре можно вычислить, как при внезапном расширении, но с введением коэффициента k (коэффициента смягчения), который учитывает, что расширение − не резкое, а постепенное.
С учетом этого получим:
|
|
|
|
|
|
1 V 2 |
|
1 |
2 V |
2 |
|
|
||||||
h |
|
|
|
1 |
|
|
|
|
1 |
k 1 |
|
|
|
1 |
|
. |
(5.11) |
|
|
|
|
2 |
|
|
|
|
|||||||||||
диф |
|
|
|
n |
|
2g |
|
n |
|
2g |
|
|||||||
|
|
|
8sin |
|
|
|
|
|||||||||||
|
Коэффициент k |
при углах раскрытия диффузора 2,5 10 можно |
||||||||||||||||
вычислять по приближенной формуле: k sin2 .
Углы раскрытия 10 в диффузорах не применяют, так как при этом возможен отрыв потока от стенок, образование мощных вихрей и резкое увеличение гидравлических потерь. Это происходит потому, что в диффузоре жидкость движется от сечения с меньшим давлением к сечению с большим давлением. Такое движение возможно только при достаточно высоких скоростных напорах. В центре потока скорости всегда высоки, а у стенок − весьма малы; поэтому там возникают обратные токи (см. эпюру скоростей на рис. 5.4, b). Они и приводят к отрыву от стенки.
5.3. Расчет истечения через отверстия и насадки
Процессы истечения в гидравлических системах широко применяются
(например, при конструировании форсунок для сжигания жидкого топлива в котельных установках, водосбросных сооружений, пожарных стволов, гидромониторов для размыва грунта и т.д.).
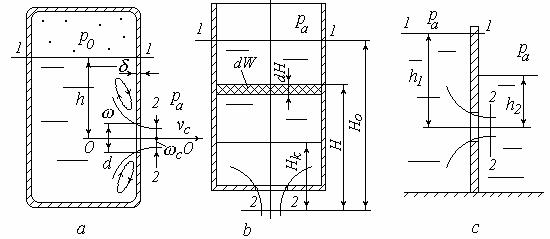
5.3.1. Истечение жидкости через отверстие в тонкой стенке
Истечение при постоянном напоре из замкнутого сосуда показано на рис. 5.5, а). Стенка считается тонкой, если ее толщина не превышает 0,2d (d − диаметр отверстия). Глубину расположения отверстия h и абсолютное давление газа над жидкостью р0 считаем постоянными. Поэтому процесс истечения − установившийся, и к нему можно применить уравнение Бернулли. Истечение происходит в атмосферу (наружное давление равно ра ).
При истечении через отверстие линии тока искривляются, из-за чего происходит сжатие струи (площадь ее сечения с меньше площади отверстия). Отношение c / называется степенью сжатия струи и обозначается . При совершенном сжатии струи (когда площадь отверстия мала по сравнению с сечением сосуда, а само отверстие расположено далеко от дна) для отверстия в тонкой стенке 0,64.
Рис. 5.5. Истечение через отверстие в тонкой стенке
Запишем уравнение Бернулли для сечений 1−1 и 2−2 (рис. 5.5, а):
|
p |
0 |
|
p |
a |
|
V |
2 |
|
V 2 |
|
h |
|
|
|
|
2 2 |
o |
2 |
. |
|||
|
|
|
|
|
|
||||||
|
g |
g |
2g |
|
|
2g |
|||||
Здесь o − коэффициент местного сопротивления отверстия (путевые потери отсутствуют).
Перепишем это уравнение в следующем виде:
|
p |
0 |
p |
a |
|
|
V |
2 |
|
|
|
h |
|
|
( 2 |
o |
) |
2 |
|
. |
(5.12) |
||
|
|
g |
|
|
|
||||||
|
|
|
|
|
|
|
2g |
|
|||

Обозначим H h |
|
p0 |
pa |
h |
p0 |
изб |
. |
|
|
|
|
(5.13) |
||||||||||||||
|
|
|
g |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
||||||||||
Величина Н называется начальным напором. Из (5.12) получим: |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V |
|
|
2gH |
|
|
|
|
|
|
1 |
|
|
|
. |
|
|||||||||||
|
|
|
|
|
|
|
2gH |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
( 2 o ) |
|
||||||||||||||||
2 |
|
|
|
( 2 o ) |
|
|
|
|
|
|
||||||||||||||||
Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
(коэффициент скорости). |
(5.14) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
( 2 o ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
При истечении через отверстие в тонкой стенке 0,97. |
|
|||||||||||||||||||||||||
В итоге получим формулу для скорости истечения: |
|
|||||||||||||||||||||||||
V2 |
2gH |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(5.15) |
|||||||||||
Расход при истечении через отверстие равен: |
|
|
|
|
||||||||||||||||||||||
Q cV2 |
|
|
. |
|
|
|
(5.16) |
|||||||||||||||||||
|
2gH |
|
|
|
||||||||||||||||||||||
Обозначим (коэффициент расхода). Тогда из (5.16) получим: |
|
|||||||||||||||||||||||||
Q |
|
. |
|
|
|
|
|
|
|
|
|
|
|
(5.17) |
||||||||||||
2gH |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
При 0,64 и 0,97 |
коэффициент расхода 0,62. |
|
||||||||||||||||||||||||
Следует отметить, что приведенные численные значения коэффициентов относятся к турбулентному режиму. При ламинарном режиме истечения эти коэффициенты зависят от числа Рейнольдса.
Истечение при переменном напоре показано на рис. 5.5, b. Здесь обозначены через Н0 , Нк , Н соответственно начальное, конечное и текущее значение напора Н, который уменьшается по мере вытекания жидкости из сосуда. Площадь сечения сосуда обозначим S, площадь отверстия – ω. Движение при этом неустановившееся, и уравнение Бернулли, строго говоря, применять в этом случае нельзя. Однако в течение бесконечно малого отрезка времени dt напор изменяется пренебрежимо мало; поэтому на данном отрезке движение можно считать квазиустановившимся (как бы установившимся) и применять уравнение Бернулли.
Пусть за время dt уровень опустился на dH; при этом вытек объем dW SdH (знак минус стоит, так как приращение dH отрицательно). С другой стороны, dW Qdt. Приравняем эти выражения.
SdH 
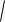 2gH dt.
2gH dt.
Отсюда
|
|
|
|
|
|
|
|
SdH |
|
|
|
|
|
|
S |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
H |
2dH . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2gH |
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Найдем время вытекания жидкости при изменении напора от Н0 |
до Нк |
|||||||||||||||||||||||||||||||||||||
Hk |
|
S |
|
|
1 |
|
|
|
|
S |
|
H0 |
|
|
|
1 |
|
|
|
2S |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
:t |
|
|
H 2dH |
|
|
|
|
|
H 2dH |
|
|
( H0 Hk ). |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2g |
2g |
|
|
|||||||||||||||||||||||||||||||||
H0 |
|
|
|
|
|
|
|
|
Hk |
|
|
|
|
|
|
|
|
|
2g |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При полном вытекании (Hk |
0) |
|
t 2S |
|
|
|
H0 |
/( |
2g |
). |
(5.18) |
|||||||||||||||||||||||||||

Подсчитаем время полного вытекания при постоянном напоре Н0 :
t |
W |
|
SH0 |
|
|
S H0 |
|
(5.19) |
||
|
|
|
|
|
|
|
||||
|
Q |
2gH0 |
|
|
2g |
|
|
|||
Сравнив (5.18) и (5.19), видим, что в последнем случае время вытекания в два раза меньше.
Истечение под уровень происходит, например, при водосбросе из одного водоема в другой (рис. 5.5, с).
В отличие от предыдущих случаев истечение происходит не в атмосферу, где p pa, а в жидкость, где давление равно p pa gh2 .
Из уравнения Бернулли получим
|
p |
a |
|
p |
a |
gh |
V |
2 |
|
V 2 |
|||
h |
|
|
|
2 |
|
2 2 |
|
|
2 |
. |
|||
|
|
|
|
|
|
|
|||||||
1 |
g |
|
|
g |
2g |
|
|
o 2g |
|||||
После сокращения и приведения подобных членов получим:
|
|
|
|
|
|
|
V 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
h |
h |
( |
|
|
|
) |
|
2 |
или V |
2g(h h ), |
|
|
|
2g |
|||||||||
1 |
2 |
|
2 |
|
o |
|
|
2 |
1 2 |
|
|
где φ − коэффициент скорости, определяемый формулой (5.14). Для расхода получим формулу
Q cV2 
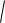 2g(h1 h2 )
2g(h1 h2 ) 
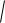 2g(h1 h2 ).
2g(h1 h2 ).
Опыты показывают, что при истечении под уровень (такое отверстие называют затопленным) коэффициенты , , можно брать такими же, как при истечении в атмосферу.
5.3.2. Истечение жидкости через насадки
Насадком называется короткий отрезок трубопровода (патрубок) определенной формы, устанавливаемый вместо отверстия для регулирования скорости истечения, расхода или того и другого. Насадки бывают цилиндрические, конические сходящиеся, коноидальные, конические расходящиеся, комбинированные.
Рассмотрим вначале истечение через цилиндрический насадок (рис. 5.6), внутренний диаметр которого равен d, площадь сечения − ω, а длина − L.

При прохождении жидкости через насадок струя вначале сжимается, затем расширяется, доходя до стенок насадка, и вытекает из него, имея диаметр d. Внутри насадка образуется вихревая зона А. Так как в сечении 2−2 площадь сечения меньше, чем на выходе (где давление равно атмосферному), то скорость там больше, чем на выходе, а давление − меньше атмосферного. Поэтому во всей зоне А устанавливается давление меньше атмосферного; она называется областью вакуума.
Запишем уравнение Бернулли для сечений 1−1 и 3−3. В отличие от истечения через отверстие, здесь, кроме местных потерь, имеются путевые.
|
|
|
p |
0 |
|
|
p |
a |
|
|
V 2 |
|
L |
V |
2 |
|
|
V 2 |
|
||||||||||
h |
|
|
|
|
|
3 3 |
|
|
|
|
|
3 |
|
|
|
н |
3 |
. |
|
||||||||||
|
|
g |
|
2g |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
g |
|
|
|
|
|
d 2g |
|
2g |
|
|||||||||||||||||
Введя обозначение Н в соответствии с формулой (5.16), получим |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
V 2 |
|
|
|
|
||||||||||
|
|
|
|
H |
|
3 |
|
|
|
|
|
н |
3 |
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
d |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|||||
Отсюда V3 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2gH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
− коэффициент скорости насадка. |
(5.20) |
|||||||||||||
|
|
|
|
L |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из этой формулы видно, что при увеличении длины насадка коэффициент скорости, а, значит, и скорость истечения уменьшаются. Поэтому чем короче насадок, тем лучше. Однако при очень малой его длине (меньшей, чем длина зоны вакуума) в эту зону зайдет атмосферный воздух, вакуум исчезнет, струя отойдет от стенки, и насадок будет работать как обычное отверстие. Оптимальной является длина насадка, равная (3…4)d. При этом 0,82.
После выхода из насадка сжатия струи нет, поэтому 0,82.
Расход через насадок равен Q 
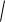 2gH .
2gH .
Сравнивая формулы для скорости истечения и расхода через насадок и отверстие, видим, что они одинаковы. Поэтому при равных Н и ω скорость истечения определяется коэффициентом φ , а расход − коэффициентом .
Цилиндрический насадок, как и любой другой насадок, имеющий в каком-либо месте площадь сечения меньше, чем на выходе, подвержен опасности возникновения кавитационного режима.
Найдем условия его возникновения для данного насадка, составив уравнение Бернулли для сечений 1−1 и 2−2. При этом учтем только местные потери при входе струи в насадок (они такие же, как при входе в отверстие).
|
|
p |
p |
2 |
|
V |
2 |
|
V |
2 |
|
|
|
|
h |
|
0 |
|
|
|
2 2 |
|
o |
2 |
|
. |
|
(5.21) |
|
|
|
|
|
2g |
|
|
|
|
||||||
|
|
g |
g |
|
|
2g |
|
|
||||||
Из уравнения постоянства расхода V2 2 |
V3 3. Но 2 |
3. |
||||||||||||
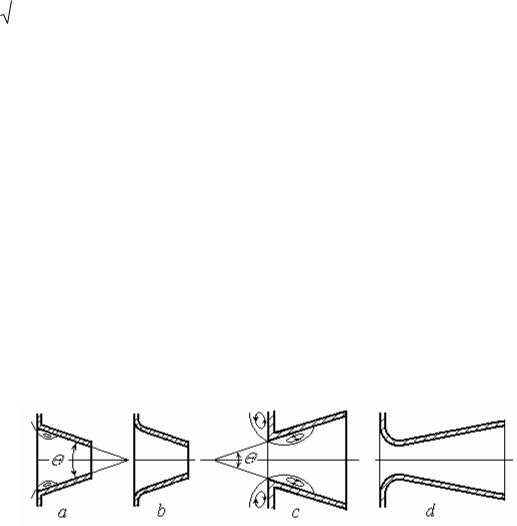
Поэтому V2 V3 |
/ . Подставив это значение V2 |
в (5.24), получим: |
||||||||||||
|
|
|
|
|
|
|
p |
0 |
p |
2 |
|
|
|
|
( |
2 |
|
o |
) |
V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(5.22) |
|||||||||||
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
. В формуле (5.25) к левой части прибавим и отнимем pa / g |
и учтем, что |
||||||||||||||||||||||||||||||||||||||||||||||||||||
V3 |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2gH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
h |
p |
0 |
p |
a |
|
|
|
|
p |
a |
p |
2 |
|
|
|
( |
2 |
|
o |
) |
|
|
2 |
2gH |
или |
|
|
|
||||||||||||||||||||||||
|
|
|
|
g |
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2g |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
H |
p |
a |
|
p |
2 |
|
|
|
|
( |
2 |
|
o |
) |
|
2 |
2gH |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
pa p2 |
|
|
( 2 |
o ) |
|
|
|
2 |
|
2gH |
|
|
|
|
|
|
|
|
|
( 2 o ) |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
H |
|
|
1 H . (5.23) |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Подставив в это выражение значения всех коэффициентов, можно найти, что численное значение выражения в квадратных скобках составляет 0,735. Тогда из (5.23) получим:
pa p2 0,735 gH ; p2 pa 0,735 gH .
Для воды при p2 pнп можно получить предельное значение напора, при котором возникнет кавитация: Hmax 13,6м.
Рассмотрим теперь другие виды насадков (рис.5.7).
Рис.5.7. Виды насадков
Конический сходящийся насадок (рис. 5.7, а) применяется там, где требуется получить компактную струю с большим расходом и большой скоростью истечения (с большой кинетической энергией и дальнобойностью).
На входе в насадок образуется небольшая вихревая зона. Коэффициенты и зависят от угла Θ. При оптимальном значении 13 24 0,95...0,96. Коноидальный насадок (рис. 5.7, b) по форме соответствует коническому сходящемуся, но имеет плавно скругленный вход для уменьшения местных потерь. Применяется там же, где предыдущий; 0,97...0,98.
Конический расходящийся насадок (рис. 5.7, с) применяется там, где требуется получить большой расход при небольшой скорости истечения, например, в дождевальных установках, трубах под насыпями дорог (чтобы уменьшить размыв грунта). При входе в насадок линии тока огибают острый угол, в результате чего образуется весьма объемная зона вакуума. В насадке
происходит дополнительный подсос жидкости из резервуара, благодаря чему коэффициент расхода, приведенный к площади 1, больше единицы.
Угол расхождения насадка не должен превышать 8…10 град, иначе возможен отрыв потока от его стенок. При этом насадок будет работать в режиме обычного отверстия.
Для такого насадка возможен кавитационный режим. Комбинированный насадок (рис. 5.7, d) представляет собой комбинацию коноидального и конического расходящегося насадка. Применяется для истечения газов и пара (сопло Лаваля).
При так называемом надкритическом перепаде давлений между сосудом и внешней средой в узком сечении такого насадка устанавливается скорость, равная скорости звука. В этом случае при расширении газового потока скорость газа не уменьшается (как у жидкости), а увеличивается и в несколько раз может превышать звуковую. Применение такого сопла, например, в ракетных двигателях позволяет получить большую реактивную силу (тягу) двигателя.
Применение сопел Лаваля в пропарочных камерах при изготовлении сборного железобетона, предложенное доцентом кафедры «Гидравлика и теплотехника» ИжГТУ В.А. Шумиловым и внедренное на десятках предприятий страны, позволяет существенно повысить интенсификацию процесса и снизить потребное время обработки.
5.4. Взаимодействие потока жидкости со стенками канала
Выше рассматривалось применение теоремы о количестве движения для решения некоторых задач гидродинамики.
Рассмотрим применение этой теоремы для определения реакции стенки криволинейного канала при протекании по нему жидкости в установившемся режиме (рис. 5.8, а). В канале выделим объем между сечениями 1-1 и 2-2.
За время dt жидкость из сечения 1 − 1 пройдет путь ds1 и переместится в положение 1 1 , жидкость из сечения 2 2 пройдет путь ds2 и
переместится в положение 2 2 . Объем, расположенный между сечениями 1 1 и 2 2 , входит как в начальное, так и в конечное положение выделенного объема. Поэтому можно полагать, что заштрихованный объем dW1 перешел в положение dW2.
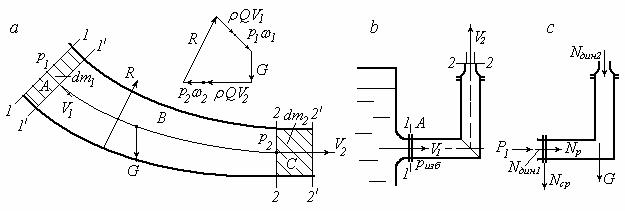
Рис. 5.8. К определению сил взаимодействия потока со стенками канала
Масса dm1объема dW1 равна dW1 1ds1 1V1dt Q1dt. Масса dm2объема dW2 равна dW2 2ds2 2V2dt Q2dt .
Так как при установившемся движении Q1 Q2, то dm1 dm2 dm Qdt.
Изменение количества движения массы dm равно dm(V2 V1).
Результирующая сила P , действующая на выделенный объем, равна:
P P1 P2 G R. (5.24)
Здесь P1 – сила от давления p1 в сечении 1–1; P2 – сила от давления жидкости в сечении 2 – 2; G – вес жидкости в выделенном объеме; R – реакция стенки.
Составим уравнение теоремы о количестве движения: |
|
dm(V2 V1) (P1 P2 G R)dt |
(5.25) |
или |
|
QdtV2 QdtV1 (P1 P2 G R)dt. |
(5.26) |
Сократив на dt, получим: |
|
QV2 QV1 P1 P2 G R. |
(5.27) |
Обозначим N R (сила действия жидкости на стенку); из (5.27) получим: |
|
N P1 P2 G QV1 QV2 . |
(5.28) |
В уравнении (5.28) P1,P2,G − статические составляющие.Они |
|
складываются векторно. Модуль P1равен p1 1, модуль P2 равен |
p2 2 |
(давления берутся в избыточной шкале). Слагаемые QV1, QV2 − динамические составляющие.
Графическое решение этого уравнения с помощью многоугольника сил показано на рис. 5.8, а.
Пример. Жидкость вытекает из закрытого сосуда через колено и насадок в атмосферу (рис. 5.8, b). Найти силы, нагружающие болты фланцевого соединения колена. Весом жидкости и колена с насадком пренебречь.
Обозначим Nдин1 QV1; Nдин2 QV2 . Направление силы Nдин1
совпадает с направлением вектора скорости V1 ; сила Nдин2 направлена обратно вектору скорости и называется реактивной силой струи. P2 0, так как p2 pa 0.
Силу воздействия жидкости на колено N в сечении, где оно стыкуется с ответным фланцем бака, разложим на вертикальную составляющую (срезающую болты) Ncp и горизонтальную составляющую (растягивающую
болты) Np . Уравнение (5.28) в проекциях на горизонтальное и вертикальное направление соответственно запишутся как
Np p1 1 QV1 и |
Ncp QV2. |
Эти выражения и составляют решение задачи.
5.5. Сила действия жидкостной струи на преграду
Определим силу от давления свободной струи жидкости, вытекающей из отверстия или насадка, на преграду в виде стенки или какого-либо тела.
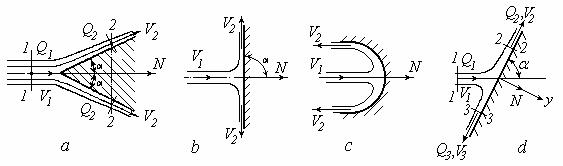
Рис.5.9. Воздействие струи жидкости на преграды различной формы
Вначале рассмотрим преграду в форме конуса, ось которого совпадает с осью струи (рис. 5.9, а). В потоке проведем сечение 1−1 и кольцевое сечение конической формы 2−2. Рассматриваем выделенный этими сечениями объем струи как поток жидкости, к которому применим теорему о количестве движения в форме (5.28):
N P1 P2 G QV1 QV2 .
Так как давление в сечениях 1−1 и 2−2 равно атмосферному, то силы P1 и P2 равны нулю. Весом выделенного участка струи пренебрегаем. Тогда статическая реакция Nст P1 P2 G 0; динамическая реакция
Nдин QV1 QV2. |
(5.29) |
Если пренебречь различием высот в сечениях 1−1 и 2−2, то из уравнения Бернулли получим, что V1 V2.
Ввиду осевой симметрии потока сила его действия на коническую преграду направлена вдоль ее оси. Спроектировав на эту ось Nдин , получим:
