
4. График функции.
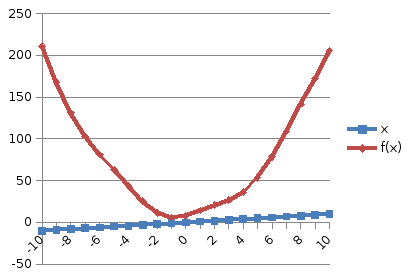
В ходе выполнения данной задачи была сформирована следующая таблица аргументов и значений функции. f(-10) =$A$2*SIN(D2)+$B$2*D2^2+$C$2 f(10) =$A$2*SIN(D22)+$B$2*D22^2+$C$2.
|
a= |
b= |
c= |
x |
f(x) |
|
5 |
2 |
8 |
-10 |
210,7201 |
|
|
|
|
-9 |
167,9394 |
|
|
|
|
-8 |
131,0532 |
|
|
|
|
-7 |
102,7151 |
|
|
|
|
-6 |
81,39708 |
|
|
|
|
-5 |
62,79462 |
|
|
|
|
-4 |
43,78401 |
|
|
|
|
-3 |
25,2944 |
|
|
|
|
-2 |
11,45351 |
|
|
|
|
-1 |
5,792645 |
|
|
|
|
0 |
8 |
|
|
|
|
1 |
14,20735 |
|
|
|
|
2 |
20,54649 |
|
|
|
|
3 |
26,7056 |
|
|
|
|
4 |
36,21599 |
|
|
|
|
5 |
53,20538 |
|
|
|
|
6 |
78,60292 |
|
|
|
|
7 |
109,2849 |
|
|
|
|
8 |
140,9468 |
|
|
|
|
9 |
172,0606 |
|
|
|
|
10 |
205,2799 |
5.
Массив
функции .
F(0,1;0,1)
=2*$A2^3*B$1+2*$A2*B$1^3
F(1;1) =2*$A11^3*K$1+2*$A11*K$1^3.
.
F(0,1;0,1)
=2*$A2^3*B$1+2*$A2*B$1^3
F(1;1) =2*$A11^3*K$1+2*$A11*K$1^3.
|
X\Y |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
0,1 |
0,0004 |
0,002 |
0,006 |
0,0136 |
0,026 |
0,0444 |
0,07 |
0,104 |
0,1476 |
0,202 |
|
0,2 |
0,002 |
0,0064 |
0,0156 |
0,032 |
0,058 |
0,096 |
0,1484 |
0,2176 |
0,306 |
0,416 |
|
0,3 |
0,006 |
0,0156 |
0,0324 |
0,06 |
0,102 |
0,162 |
0,2436 |
0,3504 |
0,486 |
0,654 |
|
0,4 |
0,0136 |
0,032 |
0,06 |
0,1024 |
0,164 |
0,2496 |
0,364 |
0,512 |
0,6984 |
0,928 |
|
0,5 |
0,026 |
0,058 |
0,102 |
0,164 |
0,25 |
0,366 |
0,518 |
0,712 |
0,954 |
1,25 |
|
0,6 |
0,0444 |
0,096 |
0,162 |
0,2496 |
0,366 |
0,5184 |
0,714 |
0,96 |
1,2636 |
1,632 |
|
0,7 |
0,07 |
0,1484 |
0,2436 |
0,364 |
0,518 |
0,714 |
0,9604 |
1,2656 |
1,638 |
2,086 |
|
0,8 |
0,104 |
0,2176 |
0,3504 |
0,512 |
0,712 |
0,96 |
1,2656 |
1,6384 |
2,088 |
2,624 |
|
0,9 |
0,1476 |
0,306 |
0,486 |
0,6984 |
0,954 |
1,2636 |
1,638 |
2,088 |
2,6244 |
3,258 |
|
1 |
0,202 |
0,416 |
0,654 |
0,928 |
1,25 |
1,632 |
2,086 |
2,624 |
3,258 |
4 |
Поверхность
функции .
.

6. Окно средства «Подбор параметра».

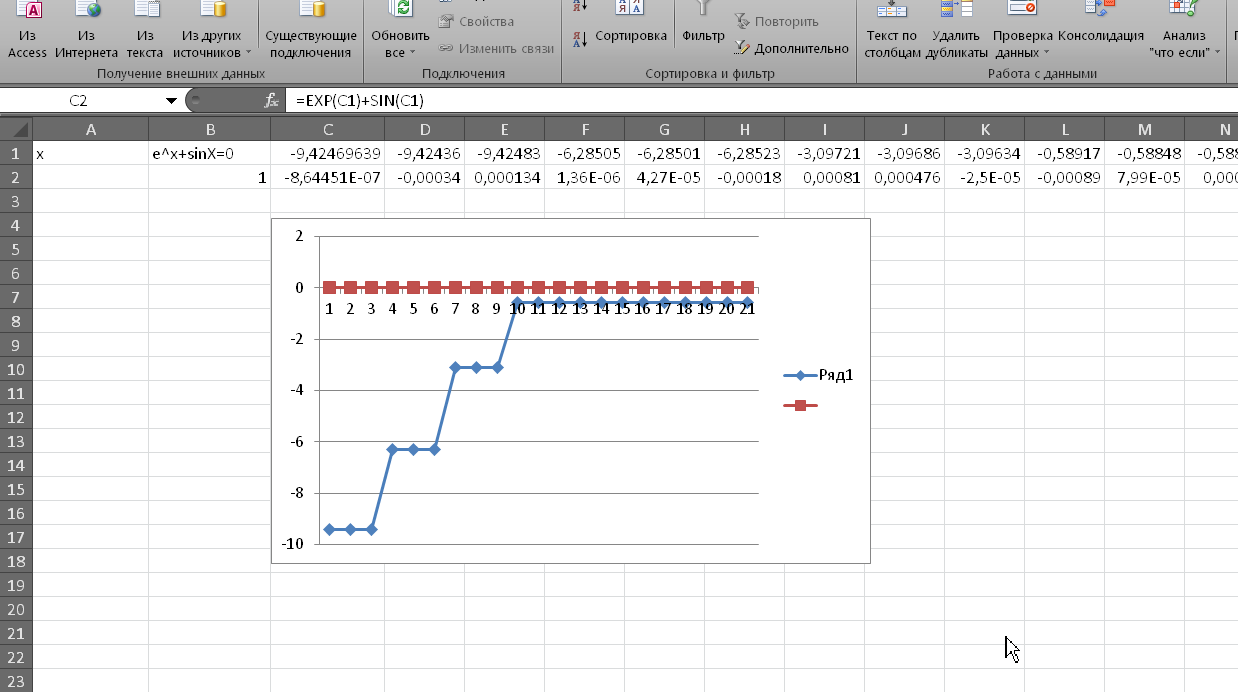
Результаты
расчетов и график приближенного решения
уравнения .
.
Формула для расчета: =EXP(C1)+SIN(C1).
7. В ходе решения данной задачи была сформирована следующая математическая модель:
x1-4 – количество домов типа Д-1 – Д-4.
830x1+835x2+360x3+45x4min

Формулы решения: =B3*B$10+C3*C$10+D3*D$10+E3*E$10 =B8*B$10+C8*C$10+D8*D$10+E8*E$10
Окно средства «Поиск решения».

Результат решения представлен на следующем рисунке.

Результатом
оптимизации стал следующий ответ:
 ,
что во много раз меньше заданного 40
000 000. По условию поиска решения x3
– целое число, но в результате оптимизации
получено минимальное значение. Таким
образом, следует округлить значение x3
в большую сторону, не смотря на его малую
величину, то есть до 360.
,
что во много раз меньше заданного 40
000 000. По условию поиска решения x3
– целое число, но в результате оптимизации
получено минимальное значение. Таким
образом, следует округлить значение x3
в большую сторону, не смотря на его малую
величину, то есть до 360.
Конечным ответом по оптимизации будет: 83 720+360 = 84 080.
ВЫВОДЫ
В лабораторной работе удалось решить все поставленные задачи. В ходе выполнения данной лабораторной работы были использованы все основные способы и средства решения задач табличным процессором Excel, и их возможном спектре.
Лабораторная работа позволила мне закрепить теоретические знания и получить необходимый опыт для использования его в дальнейшей профессиональной деятельности.
