
- •Введение
- •1.1 Уравнения механического движения
- •1.2 Расчетные схемы механической части электропривода
- •1.3. Многомассовые механические системы
- •1.4 Установившееся движение электропривода.
- •1.5. Неустановившееся движение электропривода при постоянном динамическом моменте
- •1.6. Неустановившееся движение электропривода при линейной зависимости моментов двигателя и исполнительного органа от скорости
- •1.7. Неустановившееся движение электропривода при произвольной зависимости динамического момента от скорости
- •1.8. Оптимизация передаточного числа редуктора
1.7. Неустановившееся движение электропривода при произвольной зависимости динамического момента от скорости
В общем случае динамический момент, определяемый моментами двигателя и исполнительного органа, зависит от скорости, положения исполнительного органа и времени, в том числе и произвольным образом.
Рассмотрим неустановившееся движение, когда аналитическая зависимость динамического момента от скорости отсутствует.
Нахождение искомых зависимостей M(t), (t) и (t) связано с решением (интегрированием) основного уравнения движения (1.11) при заданных законах изменения моментов двигателя и нагрузки. Если эти законы выражаются аналитически, то основные проблемы имеют математический, характер и связаны с интегрированием уравнения (1.11). Когда законы изменения моментов не заданы аналитически или точное решение (1.11) невозможно, используются приближенные способы интегрирования уравнения движения: численные и графоаналитические. Рассмотрим применение этих методов при произвольной зависимости моментов, только от скорости движения.

Численные методы интегрирования дифференциальных уравнений широко используются в вычислительной математике и известны под названием методов Эйлера, Рунге ‑ Кутта и др. Рассмотрим применение наиболее простого из них — метода Эйлера на примере получения зависимости (t) при пуске АД с вентилятором, механические характеристики приведены на рис. 1.13, а.
Метод Эйлера предусматривает замену дифференциалов переменных в (1.11) их приращениями, в результате чего это уравнение может быть записано в виде
![]() (1.42)
(1.42)
Для пользования этим уравнением ось скорости разбивается на ряд интервалов До,, на которых моменты АД и нагрузки (вентилятора) принимаются постоянными. Далее для удобства вычислений составляется табл. 1.1.
Таблица 1.1
-





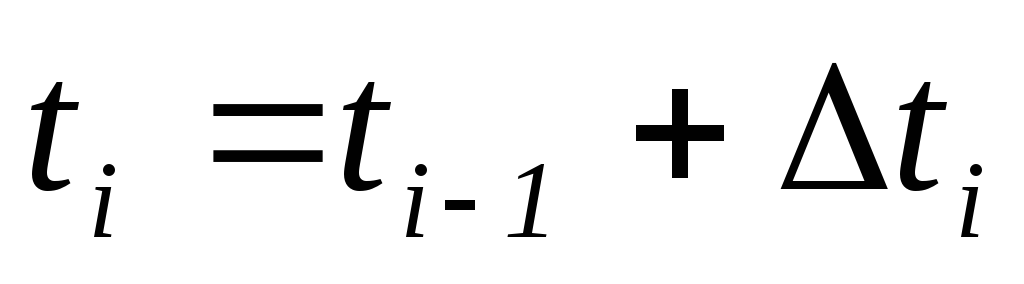
1
2
3
4
5
6

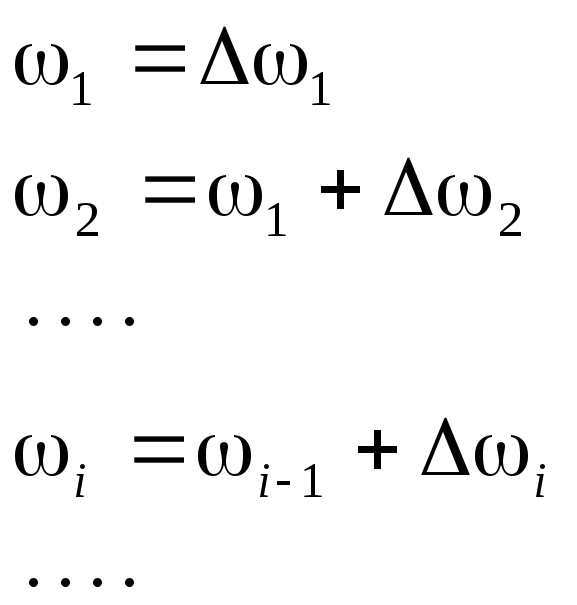




Порядок
расчета зависимости (t)
состоит в следующем. Для каждого i-го
интервала скорости
![]() по характеристикам рис. 1.13,а
определяют средние на этом интервале
моменты двигателя Mi
(столбец 3) и нагрузки МCi
(столбец 4). Далее по (1.42) рассчитывают
по характеристикам рис. 1.13,а
определяют средние на этом интервале
моменты двигателя Mi
(столбец 3) и нагрузки МCi
(столбец 4). Далее по (1.42) рассчитывают
![]() (столбец 5). На последнем этапе расчета
определяют текущие значения скорости
(столбец 2) и времени (столбец 6) как сумму
приращения и значения переменной на
предыдущем участке и строят искомую
зависимость(t)
(рис. 1.13, б). Данные табл. 1.1 позволяют
построить и зависимость M(t),
для чего должны быть использованы
данные столбцов 3 и 6.
(столбец 5). На последнем этапе расчета
определяют текущие значения скорости
(столбец 2) и времени (столбец 6) как сумму
приращения и значения переменной на
предыдущем участке и строят искомую
зависимость(t)
(рис. 1.13, б). Данные табл. 1.1 позволяют
построить и зависимость M(t),
для чего должны быть использованы
данные столбцов 3 и 6.
При
необходимости построение зависимости
(t)
уравнение
![]() также записывается в приращениях
также записывается в приращениях![]() ,
и по данным столбцов 2 и 5 может быть
получена и эта зависимость.
,
и по данным столбцов 2 и 5 может быть
получена и эта зависимость.
Достоинство
рассмотренного численного метода
состоит в его простоте и наглядности,
а точность его определяется интервалами
![]() разбиения оси скорости.
разбиения оси скорости.
Графические и графоаналитические методы, среди которых наибольшее распространение получили метод площадей и метод пропорций, также предназначены для приближенного интегрирования уравнения движения для получения зависимостей M(t), (t) и (р(0. Рассмотрим сущность метода пропорций на том же примере пуска АД вентилятора.
В основе этого метода также лежит представление переменных в (1.11) в виде приращений
![]() (1.43)
(1.43)
Построение осуществляется следующим образом (рис. 1 14). В левом квадранте строим характеристики М(), Мс() и графически находим зависимость динамического момента от скорости Мдин().

Далее
ось скорости разбиваем на ряд интервалов,
на. каждом из которых динамический
момент принимается постоянным. Затем
полученные на каждом интервале значения
Мдин
в определенном масштабе тм
откладываем по оси ординат, получаем
отрезки OM1,
OM2
и т. д. На оси абсцисс в масштабе т,
откладываем пропорциональный моменту
инерции J
отрезок ON
и точку N
соединяем с точками
![]() и т. д. Далее из начала координат проводим
прямуюОА1,
параллельную NM1,
до пересечения с горизонтальной линией,
соответствующей верхней границе первого
интервала скорости. Этот отрезок ОА1
представляет собой график скорости
(t)
на первом интервале движения.
и т. д. Далее из начала координат проводим
прямуюОА1,
параллельную NM1,
до пересечения с горизонтальной линией,
соответствующей верхней границе первого
интервала скорости. Этот отрезок ОА1
представляет собой график скорости
(t)
на первом интервале движения.
Действительно,
![]() ,
но
,
но![]()
![]() ;ON~J;
;ON~J;
![]() ~
~![]() ,
следовательно, в соответствии с (1.43)
,
следовательно, в соответствии с (1.43)![]() ~
~![]() .
.
Аналогичным построением для остальных участков разбиения оси скорости может быть получена искомая кривая (t), показанная в первом квадранте рис. 1.14.
Отметим одно обстоятельство, которое должно учитываться при использовании этого метода. В соответствии с (1.43) масштабы тм , тJ ,т и mt; должны быть связаны между собой соотношением
![]() (1.44)
(1.44)
Поэтому независимо от остальных могут быть выбраны только масштабы трех величин, а масштаб четвертой должен быть определен из пропорции (1.44).
