3.5. Радиус инерции сечения

Радиус инерции сечения выражается следующим образом:

.

Радиус инерции можно представить как расстояние от оси z до точки, в которой необходим сосредоточить всю площадь сечения, чтобы момент инерции этой точки был равен моменту инерции всего сечения.

Радиусы инерции, соответствующие главным осям, называются главными радиусами инерции сечения:

; .

Вопросы для повторения

1. Что называется статическим моментом сечения?

2. Какую размерность имеет статический момент сечения?

3. Как определяют координаты центра тяжести сложного сечения?

4. Что называют осевым, центробежным, полярным моментами инерции сечения?

5. Размерность моментов инерции сечения?

6. Чему равна сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей?

7. От чего зависит знак центробежного момента инерции сечения?

8. Какие оси называют главными осями инерции?

9. Как определяют положение главных осей и главные моменты инерции?

10. Чему равен центробежный момент инерции относительно главных осей инерции?

11. Как определяют главные оси для сечения, имеющего хотя бы одну ось симметрии?

12. Почему производят разбивку сложного сечения на составляющие простые части при определении статических моментов и моментов инерции сечения?

13. Дайте определение радиуса инерции.

Тесты для повторения

1. Статический момент площади сечения относительно центральной оси у

(а) S_y > 0; (б) S_y < 0; (в) S_y = 0; (г) S_y 0.

Ответ: (в), потому что по определению, ось, относительно которой статический момент равен нулю, является центральной.

2. Для какой из осей статический момент сечения S будет наибольшим:

(а) – у; (б) – х₁; (в) – х₂; (г) – х₃.

Ответ: (г), так как S_y = 0, а в трех остальных случаях статический момент имеет большую величину для наиболее удаленной оси.

3. Если I_y=I_z , а D_yz=0, то оси y, z являются:

(а) центральными; (б) главными центральными;

(в) осями симметрии; (г) главными.

Ответ: (г), потому что равенство центробежного момента инерции нулю – необходимое и достаточное условие для главных осей инерции. Если оси y, z были бы центральными, то необходимым дополнением было бы: S_y=0 и S_z=0.

4. При повороте взаимно перпендикулярных осей yи z относительно начала координат сумма осевых моментов инерции I_y+I_z:

(а) зависит от угла поворота; (б) не изменяется;

(в) равна нулю; (г) изменяется, но не зависит от угла поворота.

Ответ: (б), сумма осевых моментов относительно двух ортогональных осей при их повороте остается постоянной величиной, равной полярному моменту инерции I_р=ρ² dA.

5. Ось y изменила свое направление на противоположное. Значение какого момента инерции изменится:

(а) I_y; (б) I_z; (в) D_yz; (г) I_p.

Ответ: (в), величина центробежного момента сохранится, но знак изменится на противоположный. Для других моментов инерции координаты под интегралом стоят в квадрате, следовательно, будет ли координата +y или –у – величина момента не изменится.

6. Осевой момент инерции для треугольника будет максимальным для:

(а) z₀; (б) z₁; (в) z₂; (г) z₃.

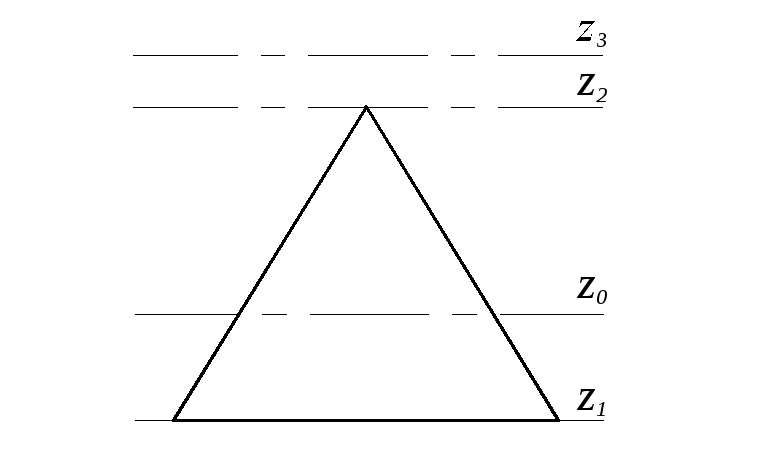
Ответ: (г), поскольку наименьшее значение осевой момент I_z имеет для центральной оси z₀, а значение осевого момента инерции для оси, параллельной центральной, возрастает на величину равную произведению площади фигуры на квадрат расстояния между осями.