14.2. Ударная нагрузка на стержень

Ударная нагрузка возникает от падения тела на деформируемую систему. Действие ударной нагрузки вначале концентрируется лишь на некотором участке длины стержня, вследствие чего деформации оказываются большими, чем при статической нагрузке. Затем эти деформации распространяются на следующий участок длины стержня, в то время как на первом участке они убывают до величины статических деформаций и т.д. В результате мы получаем волновой характер распространения деформаций, а следовательно, и напряжений по длине стержня.

Еще большие осложнения вносит пластическая деформация, так как скорость ее распространения, в отличие от упругой деформации, не постоянна, а изменяется в зависимости от направления.

Ограничимся рассмотрением случая удара, сопровождающегося только упругими деформациями, на этапе, когда последние распространяются на всю длину стержня. Для ее решения принимаем закон сохранения энергии:

П+К=const,

где П – потенциальная энергия системы, К – кинетическая энергия падающего тела. П и К – положительные величины. П достигает значения П_mах, когда К=0, К – достигает значения К_mах, когда П=0. Следовательно, К_mах=П_mах.

Рис. 40. Модель стержня, воспринимающего удар

Рассмотрим удар от тела с силой веса F, вызывающий поступательное перемещение точек системы, которая представлена в виде деформируемой невесомой пружины (рис. 40). Тело падает с высоты h_o на точку А системы. Для линейно деформируемой системы:

П_mах

где R_mах – наибольшая сила сопротивления в точке А, ∆_mах – перемещение точки А;

∆_mах= υ R_mах,

где υ – коэффициент пропорциональности, так что

П_mах

Величина К_mах равна работе груза F:

К_mах=F(h_o+∆_mах).

Итак,

или

откуда

или

где –динамический коэффициент.

Учитывая, что

,

где – скорость падения, получаем:

При = 0 (внезапное приложение груза к системе)ПолучивнаходимR_mах

Вопросы для повторения

1. Какие нагрузки называют динамическими?

2. Как определяют величины динамических напряжений?

3. Что следует предпринять, чтобы динамический коэффициент снизить?

4. Что представляет собой динамический коэффициент?

5. Что полагается в основу при выводе формул для определения перемещений при ударе?

6. Влияет ли модуль продольной упругости на величину динамических напряжений? Обоснуйте.

7. Какой вид имеет формула динамического коэффициента при ударе?

Методические указания и задачи для самостоятельного решения контрольных работ

1. Построить эпюры внутренних силовых факторов для заданных балок (рис. 41, 42), рам (рис. 43, 44) и вала (46), приняв q, F, M_e, и l в соответствии с индивидуальным заданием.

2. Для схемы (рис. 41):

- подобрать балку двутаврового поперечного сечения из стали, считая, что σ_у=240 МПа, n=1,6; ;

-построить эпюры σ и τ для опасного сечения;

-методом начальных параметров определить прогиб в точке равноудаленной от правой и левой опоры и построить примерный вид упругой линии.

3. Для схемы (рис. 42) подобрать прямоугольное сечение балки из чугуна, если высота сечения h в два раза больше ширины b, приняв, МПа, 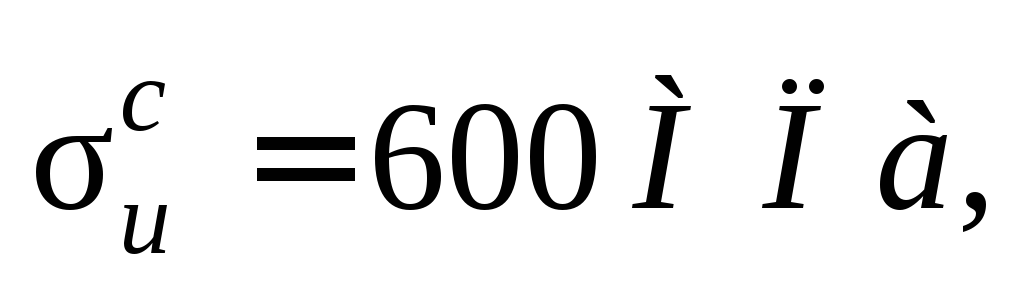n =2. Построить эпюры σ и τ для опасного сечения.

4. Для схемы (рис. 43) проверить прочность составного сечения, представленного на схеме (рис. 45) , полагая σ_adm=160 МПа.

5. Для схемы (рис. 46) подобрать размеры сплошного круглого вала на каждом из участков, полагая, что на левом участке вал кольцевого сечения и дать эскиз вала.

Таблица 1

Схема	1	2	3	4	5	6	7	8	9	0	а
столбец
F, kH	10	12	14	16	18	20	10	12	14	16	б
q,	6	7	8	9	5	6	7	8	9	10	в
Me, kH·м	8	10	12	6	8	10	12	14	16	20	а
l, м	2,2	2,4	2,6	2,0	2,8	3,0	2,0	2,4	2,6	3,0	б
h, м	2	3	4	2	3	4	2	3	4	-2,5	в

Перед выполнением контрольных работ студент должен изучить соответствующие разделы рекомендуемой учебной литературы.

Контрольная работа выполняется на стандартных листах писчей бумаги (210297 мм), сшивается в брошюру. Страницы нумеруют.

В таблице 1 даны исходные данные для расчетных схем, изображенных на рис. 41, 42, 43, 44. Возьмите последние три цифры вашей зачетки и поставьте над ними буквы вба, которые стоят в последнем столбце табл. 1. Если ваши цифры 137, то для а =7 вы берете 7-й столбец, дающий 7 схему и M_e=12 кН·м; для б=3 – 3-й столбец и F = 14кH и l =2,6м; для в=1 – 1-й столбец и q = 6 h = 2м. Схема из табл. 2 (рис. 45) принимается по последней цифре и данные табл.3 (рис.46) – по 2 цифре.

Рис. 41. Шарнирно опертые балки

Рис. 42. Балки с защемляющими опорами

Рис. 43. Рамы с защемляющими опорами

Рис. V.5

Рис. 44. Рамы с шарнирными опорами

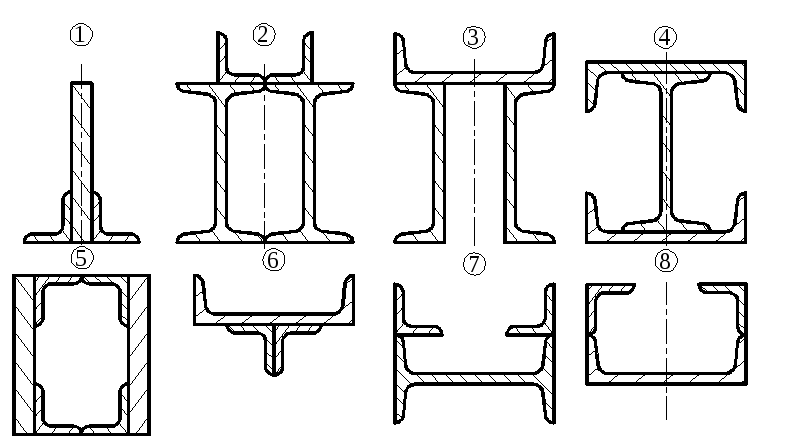
Рис. 45. Составное сечение

Таблица 2

строка	Полоса	Швеллер	Двутавр	Равнобокий уголок
Схема рис. 45
1	300	30	27
2	310	27	30
3	280	24	33
4	280	18	16
5	320	18а	18
6	320	20	20
7	320	22	24
8	300	24	27
9	300	27	30
0	300	30	33

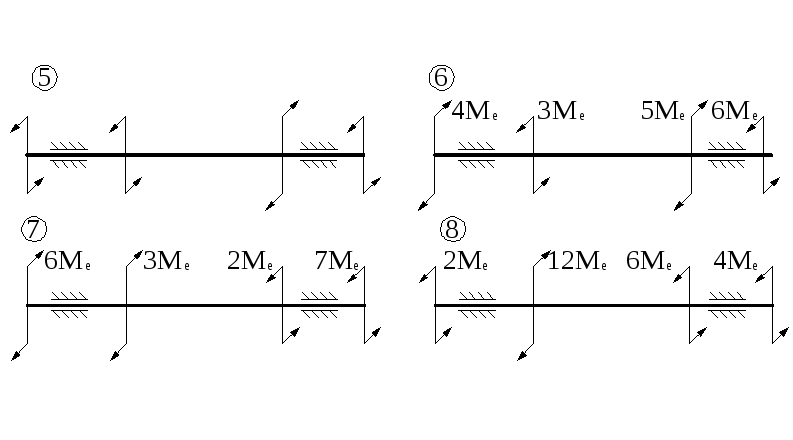
Р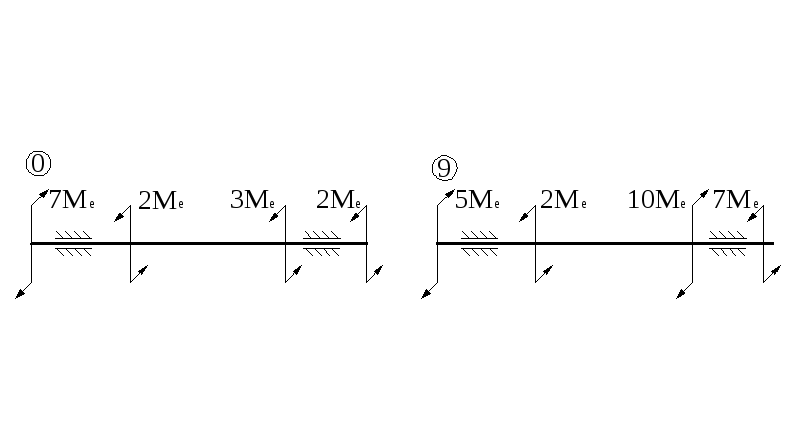ис. 46. Вал

Таблица 3

схема	1	2	3	4	5	6	7	8	9	0
столбец
Ме,кН·м	2	3	4	5	6	2	3	4	5	6
τadm, МПа	60	65	70	75	80	85	90	80	70	60
d/D	0,9	0,8	0,7	0,6	0,5	0,4	0,9	0,8	0,6	0,5