Вопросы для повторения

1. Как изменяются нормальные напряжения по высоте балки при чистом изгибе?

2. Как определить максимальные нормальные напряжения при изгибе?

3. Что называют моментом сопротивления сечения при изгибе?

4. По какому закону изменяются касательные напряжения по высоте балки прямоугольного сечения?

5. Какие формы поперечных сечений являются рациональными для балок из пластичного материала?

6. Какой должна быть рациональная форма сечения для балки из хрупкого материала?

7. Как проводится проектный расчет для балки заданной формы сечения?

8. В каких случаях следует производить дополнительный поверочный расчет по наибольшим касательным напряжениям?

Тесты для повторения

1. Чугунная балка таврового сечения нагружена изгибающим моментом, действующим в вертикальной плоскости. Определить соотношение напряжений .

(а) 2; (б) 2,5; (в) 3; (г) 3,5.

Ответ:(б). Определим величину момента инерции сечения относительно осиz, установив предварительно положение центра тяжести сечения:

y_В==10см.

Тогда:

I_z=Σ(I_zi+= += 485см⁴.

Напряжение в точке С

σ_C==.

Напряжение в точке В

σ_В==

Это напряжение превышает напряжение в точке Св:

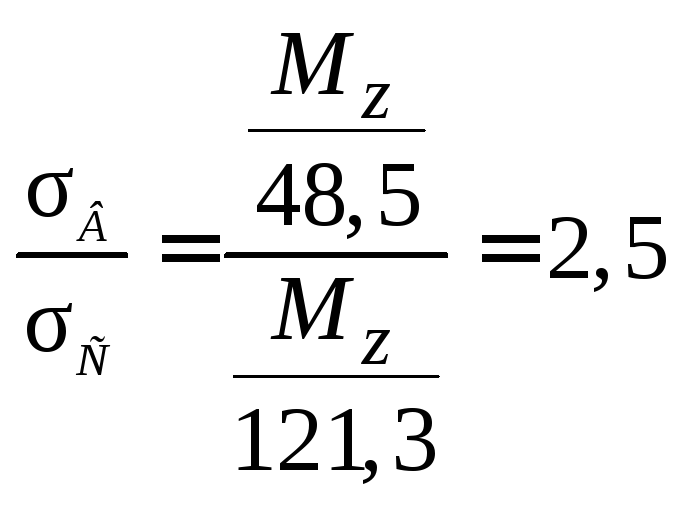раза.

2. Под действием нагрузки в вертикальной плоскости в балке, возникает изгибающий момент. Определить соотношение напряжений в сечении 1 и 2.

(а) 2,5; (б) 3; (в) 3,5; (г) 4.

Ответ:(в). Определим моменты сопротивления для сечений 1 и 2:

см³,

=

Поскольку ,,В данном случае

Контрольные тесты

1. Изгиб называется чистым, если в поперечных сечениях балки из шести внутренних усилий действуют только …

2. При изгибе возникают такие перемещения, как …

3. При поперечном изгибе в поперечных сечениях балки возникают такие напряжения, как …

4. Дифференциальная зависимость между изгибающим моментом и поперечной силой имеет вид …

5. Когда изгибающий момент на участке с распределенной нагрузкой имеет экстремальное значение, поперечная сила в этом сечении равна …

6. Нормальные напряжения в любой точке поперечного сечения балки определяются по формуле …

7. Наибольшие нормальные напряжения в поперечном сечении балки возникают в …

8. Условие прочности по нормальным напряжениям при изгибе имеет вид …

9. Касательные напряжения при поперечном изгибе в любой точке поперечного сечения балки определяется по формуле ...

10. Касательные напряжения при поперечном изгибе достигают максимума на …

11. Условие прочности по касательным напряжениям при изгибе имеет вид …

12. При упругом деформировании нейтральная линия сечения балки проходит через …

13. Момент сопротивления изгибу балки прямоугольного сечения размером в×h относительно центральной оси, параллельной основанию в равен …

10. Основные энергетические teopeмы для упругого тела. Методы определения перемещений стержневых систем

10.1. Энергетические теоремы

Обращаясь к философским категориям непрерывности и прерывности, характеризующим структуру материи, введем соответствующие понятия континуальных и дискретных систем. Для континуальных систем используется модель сплошного деформируемого твердого тела, описываемая непрерывными функциями напряжений, деформаций и перемещений. Нагрузка также имеет функциональный характер.

Предположим теперь, что на систему, находящуюся в равновесии, действует n сил F_i, приложенных в точках А_i в определенных направлениях. При этом точки А_i перемещаются в положения А'_i. Обозначим через q_i компонент перемещения А_iA'_i по направлению силы F_i. Система сил F_i представляет собой элемент (F₁, F₂,…, F_n) n-мерного векторного пространства Λ_F, а система перемещения q_i − элемент (q₁, q₂,…, q_n) n-мерного век­торного пространства Λ_q.

Предположим также, что напряженное состояние дискретной системы определяется N составляющими σ_i, а совокупность этих составляющих есть элемент (σ_1,, σ₂,…, σ_N) N-мерного векторно­го пространства Λ_σ; деформированное состояние системы опреде­ляется N составляющими ε_i, а совокупность этих составляющих есть элемент (ε₁, ε₂,…, ε_N) N-мерного векторного простран­ства Λ_ε.

Упругое тело характеризуется, прежде всего, тем, что в определенных температурных условиях при неучете фактора време­ни существует взаимно однозначная зависимость между компонен­тами F(σ) открытой выпуклой области Г_F(Г_σ) пространства Λ_F(Λ_σ) и компонентами q(ε) открытой выпуклой области Г_q(Г_ε) простран­ства Λ_q(Λ_ε):

Полагаем, как и раньше, что в естественном состоянии при отсутствии внешних сил перемещения точек системы и составляющие напряжения и деформации равны нулю. В частном случае функ­ции F_i, q_i, σ_i и ε_i могут быть линейными (линейная упругость).

Элементарная работа внутренних сил (работа на беско­нечно малом этапе деформирования) равна

Приращение этой функции с точностью до бесконечно малых второ­го порядка можно записать ее полным дифференциалом

Таким образом,

Потенциальная энергия деформации U численно равна Ũ. Сле­дова-тельно,

Вводя в рассмотрение дополнительную энергию U*, выводим:

Принцип возможных перемещений имеет выражение:

где δq_i - вариации возможных перемещений.

Так как первая вариация δ с точностью до бесконечно малых высшего порядка равна первому дифференциалу, то вариация по­тенциальной энергии деформации, выраженной через перемещения, равна

Итак,

откуда вследствие произвольности вариаций δq_i следует, что

т.е. частная производная потенциальной энергии деформации по одному из перемещений точки равна силе, совпадающей по направ­лению с перемещением и приложенной в той же точке.

Сформулированное положение представляет собой теорему Лагранжа, которая, как и сам принцип возможных перемещений, справедлива для линейно и нелинейно деформируемой системы. Природа формулы Лагранжа аналогична природе формул Грина.

Интегрируя dU = F_idq_i при условии U(0)= 0 и суммируя ре­зультаты по i, получаем

В случае P_i = k_iq_i (k_i = const) имеем

т.е. для линейно деформирующегося тела потенциальная энергия деформации, эквивалентная работе внешних статически нарастающих сил, равна полусумме произведений сил на соответствующие им перемещения.

Сформулированное положение представляет собой теорему Клапейрона. Ее аналитическое выражение аналогично по структуре формуле

для континуальной системы.

Обращаясь к принципу возможных изменений напряженного со­стояния, устанавливаем, что

т.е. частная производная дополнительной энергии по одной из сил равна перемещению точки приложения этой силы по ее направлению (теорема Кастильяно).

Для линейно деформирующегося тела (U*= U)

Ввиду независимости вторых смешанных производных иот порядка дифференцирования вытекают следующие зависимости:

В случае линейной связи между силами и перемещениями

а) первая зависимость выражает первую теорему Рэлея – тео­рему о взаимности реакций: реакция первой связи от единичного перемещения второй связи равна реакции второй связи от единичного перемещения первой связи (r_ij = r_ji);

б) вторая зависимость выражает теорему Максвелла – теорему о взаимности перемещений: перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй силы, вызванному первой силой (δ_ij = δ_ji).

Рассмотрим два случая бесконечно малых произвольных при­ращений сил F_i и перемещений q_i : dF_i', dq_i'; dF_i", dq_i", так что

(i = 1,2,…,n; j = 1,2,…,n),

где (∂q_i /∂F_j)₀ − величина производной ∂q_i /∂F_j при F_j= F_jo.

Запишем равенство

и выпишем первые три члена ряда для каждого слагаемого правой части (i=1, j=1; i=1, j=2; i=2, j=1):

Согласно первой теореме Рэлея, (∂q₁/∂F₂)₀ = (∂q₂/∂F₁) ₀ и выпи­санная сумма, как и вся правая часть равенства, обращается в нуль. В итоге получаем

Это равенство выражает следующую теорему: при некотором состо­янии равновесия упругой системы двум различным случаям беско­нечно малых приращений сил соответствуют такого рода прираще­ния перемещений, что работа приращений сил первого случая на приращениях перемещений второго случая равна работе приращений сил второго случая на приращениях перемещений первого.

В случае линейной упругости (F_i= k_iq_i) имеем

После подстановки этих выражений в полученное равенство выводим

Это равенство выражает теорему Бетти - теорему о взаимно­сти работ для упругого линейно деформирующегося тела: работа первой группы сил на перемещениях по их направлениям, вызван­ных второй группой сил, равна работе второй группы сил на пе­ремещениях по их направлениям, вызванных первой группой сил.

Представив предшествующее равенство в виде

устанавливаем принцип независимости действия приращений сил:

обобщающий принцип независимости действия сил, справедливый для линейно-упругого тела.

Еще один вариант теоремы взаимности можно получить, пред­полагая, что в первом случае получила приращение только сила F_i на величину dF_i и место приложения силы F_j закреплено, а во втором случае получило приращение перемещение q_j на величину dq_j и сила F_i ос- талась неизменной. Тогда

где dF_j следует рассматривать как реакцию в точке закрепления, a dq_i – как перемещение, вызванное dq_j. В итоге

В случае линейной связи между силами и перемещениями эта зависимость выражает вторую теорему Рэлея − теорему о взаимно­сти реакций и перемещений: единичная реакция связи j от силы F_i=1 равна единичному перемещению по направлению силы F_i от перемещения связи q_j=l, взятому с противоположным знаком (r_{i j}= – δ_ji).

Теоремы взаимности находят практическое использование, в частности, при расчете статически неопределимых систем.