4.3. Понятие о деформации

Следует различать деформации и перемещения. Перемещение – изменение положения точки в пространстве. Деформация – изменение формы и размеров тела.

Деформации могут быть угловыми и линейными (рис. 12).

Рис. 12. Линейная и угловая деформация

Линейная деформация характеризует изменение размеров тела: ε = ∆l/l.

Угловая деформация характеризует изменение формы тела и чаще всего называется углом сдвига. Угол сдвига – это изменение первоначально прямого угла .Полная деформация представляется как сумма линейной и угловой деформаций.

4.4. Типы напряжено-деформированного состояния

В зависимости от приложенных к телу нагрузок и вызываемых ими внутренних сил выделяют несколько типов деформаций, различающихся законом распределения напряжений по сечению тела.

1. Растяжение-сжатие –в поперечном сечении действует только одно внутреннее усилие, не равное нулю, – продольная сила.

2. Сдвиг –в поперечном сечении действует только поперечная сила.

3. Кручение –в поперечном сечении действует только крутящий момент.

4. Чистый изгиб – в поперечном сечении действует только изгибающий момент.Поперечный изгиб– в поперечном сечении действует изгибающий момент и поперечная сила.

5. Сложное сопротивление –одновременное действие нескольких типов простых деформаций – растяжения-сжатия, кручения, изгиба.

4.5. Закон Гука

По закону Гука перемещения прямо пропорциональны нагрузкам.

,

где F – сила, Δ – перемещение, K – жесткость, зависящая не только от свойств материала, но и от формы и размеров сечения.

На графике этот закон изображается прямой линией (рис. 13, а). – работа внешних сил;u – удельная потенциальная энергия деформации.

а б

Рис. 13. Закон Гука при растяжении: а – для сил и перемещений;

б – для напряжений и деформаций

Поскольку напряжения и деформацииесть нагрузка и перемещение, деленные соответственно на константыA и l, то и напряжения прямо пропорциональны деформациям. На графике (рис. 13, б) зависимость σ от ε изображается прямой линией. Следовательно, можно записать

,

где Е – коэффициент пропорциональности, названный модулем Юнга. Модуль Юнга Е – константа материала и приводится в справочниках. Например, для стали Е = 2 · 10⁵ МПа.

На практике часто необходимо найти удлинение стержня под действием растягивающих или сжимающих нагрузок. Подставим в запись закона Гука выражение и, тогда, откуда

.

Эта формула справедлива в случае постоянного продольного усилия N по всей длине стержня. Величина ЕА называется жесткостью при растяжении-сжатии.

Если на стержень действует несколько сосредоточенных сил, то стержень разбивается на несколько участков (от силы до силы) и полное удлинение равно сумме удлинений каждого участка в отдельности

,

где i – номер участка, n – количество участков.

В общем случае, если продольная сила на некоторых участках переменная, т. е. действует распределенная нагрузка, то удлинение пропорционально площади эпюры продольных усилий:

.

4.6. Гипотезы и допущения

В целях упрощения решения практических задач в ряде случаев принимают упрощающие гипотезы, которые приводят к простым инженерным формулам. Перечислим основные гипотезы, используемые в курсе сопротивления материалов.

Гипотеза сплошности, однородности, изотропности материалов. Пренебрегая атомно-молекулярной структурой материала, считаем его сплошным, однородным, изотропным. Материал считается:

– сплошным, если в теле нет разрывов;

– однородным, если его свойства во всех точках одинаковы;

– изотропным, если его свойства во всех направлениях одинаковы.

При этом справедлив закон Гука.

Гипотеза малости деформаций. Для всякого твердого тела деформации малы по сравнению с размерами тела. При составлении уравнений равновесия тела изменением его размеров вследствие деформации можно пренебречь.

Принцип независимости действия сил. Результат действия на тело системы сил не зависит от порядка приложения нагрузок и равен сумме результатов действия каждой силы в отдельности.

Рассмотрим балку с тремя нагрузками F, М и q (рис. 14). Суммарный прогиб конца балки (точки А) будет равен сумме прогибов балки от действия отдельно приложенных сил М, F и q:

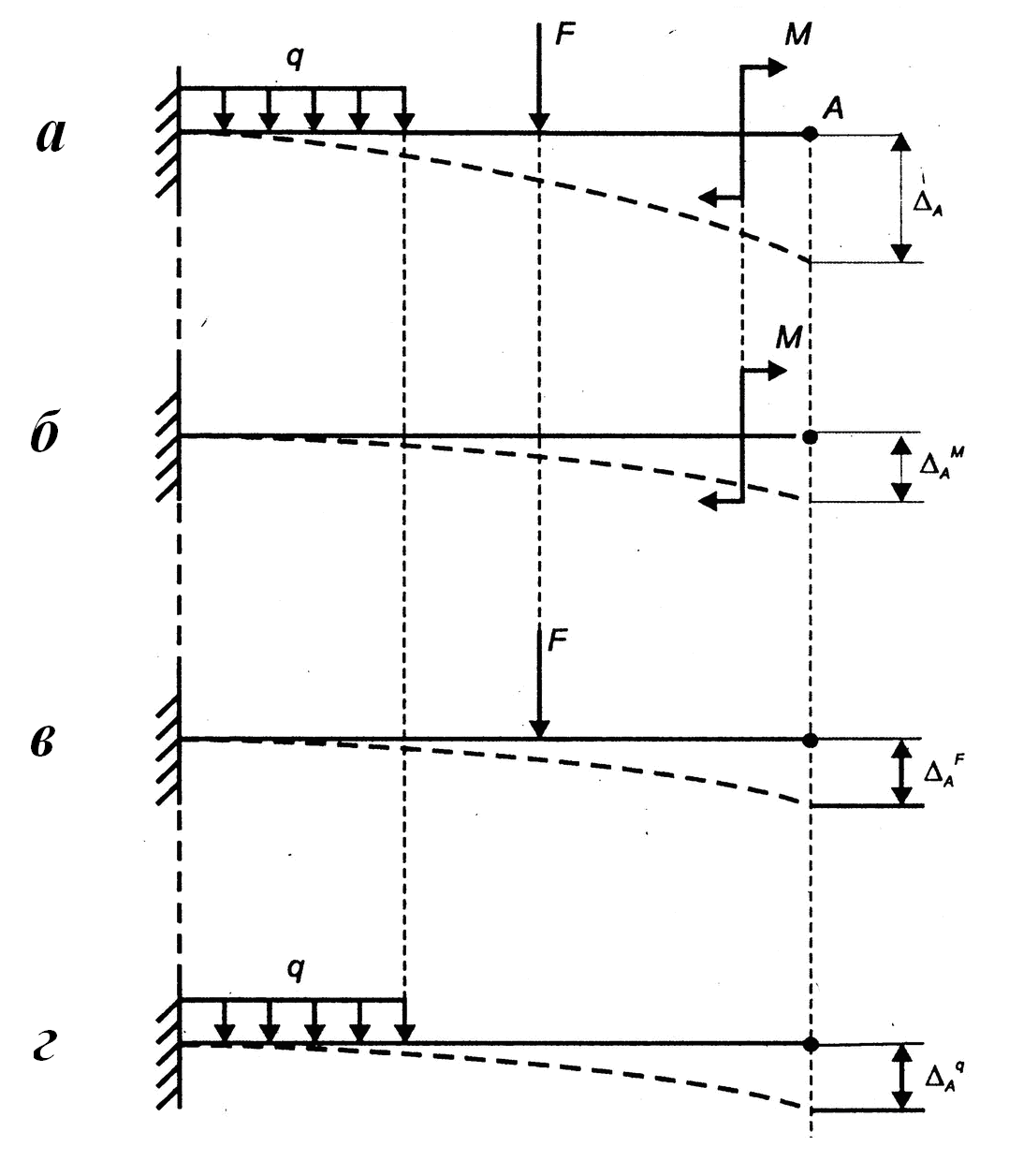
Рис. 14. Принцип независимости действия сил: а – прогиб от

заданной нагрузки; б – ,,– прогибы от ее компонентов

Гипотеза плоских сечений, относящаяся к брусьям и стержням. Сечения, плоские до деформирования остаются плоскими после деформирования.

Эту гипотезу можно рассматривать как экспериментальный факт, отражающий, например, поведение прямоугольной сетки, нанесенной на резиновый стержень (рис. 15). При его изгибе продольные линии искривляются, в то время как поперечные линии остаются прямыми.

Гипотеза отсутствия боковых давлений, т. е. давление волокон друг на друга.

Гипотеза предполагает, что нормальные напряжения σ действуют только вдоль продольной оси стержня и отсутствуют в поперечных направлениях. На самом деле напряжения σ в поперечных направлениях существуют, но они во много раз меньше, чем в продольном направлении, и для упрощения расчетов ими можно пренебречь.

Рис. 15. Гипотеза плоских сечений: а – сетка поверхности тела

до деформирования; б – она же после деформирования