
ответы на экзамен по математике(2 семестр)
.pdf
|
|
1. Вычисление объемов тел вращения. |
|
|
|
|
2. Вычисление площади поверхности вращения. |
|||||||||||||
|
|
Вычисление объема тела вращения. Если криволинейная |
|
|
|
Если дуга гладкой кривой y f x a x b вращается |
||||||||||||||
|
|
трапеция, ограниченная кривой y f x и прямыми |
|
|
|
вокруг оси Ox, то площадь поверхности вращения |
||||||||||||||
|
|
y 0, x a, x b, вращается вокруг оси Ox, то объем тела |
|
|
вычисляется по формуле b |
|
|
|
||||||||||||
|
|
вращения вычисляется по формуле |
|
|
|
|
|
|
|
|
Sx 2π y 1 y 2 dx. |
|||||||||
|
|
|
|
|
|
|
|
|
|
a |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
b |
|
|
|
|
|
|
|
Если кривая задана параметрическими уравнениями |
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
Vx π y dx. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x x t , y y t t t t |
|
, |
|||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Если фигура, ограниченная кривыми |
|
|
|
|
|
|
|
|
t2 |
|
|
|||||||
|
|
y1 f1 x и y2 |
f2 x 0 f1 x f2 x и прямыми x=a, x=b, |
|
|
|
|
Sx 2π y x2 y2 dt. |
||||||||||||
|
|
вращается вокруг оси Ox, то объем тела вращения |
|
|
|
|
|
|
t1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vx π y22 y12 |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Механические приложения определенных |
|
|
|
|
4. |
Несобственные интегралы. |
|||||||||||||
|
|
|
интегралов. |
|
|
|
|
|
|
|
Несобственные интегралы |
|||||||||
|
|
|
Вычисление работы с помощью определённого |
|
бывают 2-ух видов: |
|
|
|
|
|
|
|||||||||
|
интеграла. |
|
|
|
|
|
|
|
|
1)интервал интегрирования представляет собой бесконечность |
||||||||||
|
|
|
Пусть |
под |
|
действием |
|
некоторой |
|
|
|
|
|
∞ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ ( ) |
||||
|
силы |
материальная |
|
точка |
М движется по |
прямой |
в |
|
|
|
|
|
−∞ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
направлении оси |
. Требуется найти работу, произведённую |
|
2)хотя бы 1 из пределов является точкой разрыва интегральной |
||||||||||||||||
|
|
функции |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
силой |
|
при |
перемещении |
точки |
М |
из |
|
ТЕОРЕМА(1): не собственный интеграл |
|||||||||||
|
|
|
∫∞ ( ) является сходящимся если существует предел |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
(∫ |
|
|
|
|
|
|
|
|
положения |
в положение |
. |
|
|
|
|
lim |
( )) |
|
|
|
|
|
|
|||||
|
|
1) |
Если сила постоянна |
, то работа выражается |
|
|
→∞ |
− |
|
|
|
|
|
|
|
|||||
|
|
|
в противном случае интеграл является расходящимся |
|||||||||||||||||
|
|
|
следующим образом |
|
. |
|
|
|
|
ПРИМЕЧАНИЕ. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
В не собственных интегралах такого вида, один из пределов |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2) |
Если сила переменная величина, то |
|
. |
|
|
может быть конечным числом. |
||||||||||||
|
|
|
|
ТЕОРЕМА(2): |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ ( ) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
b-точка разрыва |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Th: Если есть не собственный интеграл где b-точка разрыва, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
тогда не собственный интеграл является сходящимся, если |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
существует предел |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim ∫ ( ) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
значение не собственного интеграла будет равняться пределу |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
если предел не существует не собственный интеграл является |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
расходящимся |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

5.Алгебраическая форма комплексного числа. 6. Тригонометрическая форма записи комплексного числа и
|
Геометрическое изображение. |
действия над числами. Формула Муавра. |
||||
Запись |
|
|
|
Абсциссу a и ординату b комплексного числа a + bi можно выразить через |
||
вида |
|
называется алгебраической или |
его модуль r и аргумент φ : |
|
||
координатной формой комплексного числа . |
|
|
||||
При этом действительное |
|
|
|
|||
число |
называется действительной |
|
|
|||
частью числа : |
, а действительное |
Правила перехода от алгебраической формы комплексного числа к |
||||
число |
- его мнимой частью: |
. |
тригонометрической |
|
||
|
|
|||||
Величина называется мнимой единицей и |
1. Находим модуль комплексного числа |
|
||||
|
|
|
|
|
||
удовлетворяет равенству |
. |
2. Для нахождения угла j сначала определяем геометрически, в какой |
||||
Для числа |
действительная |
четверти находится точка z |
|
|||
часть |
|
, а мнимая - |
. |
|
|
|
Любому комплексному числу z = a + ib можно поставить в |
3. Составляем уравнение |
и по решению одного из |
||||
соответствие точку координатной плоскости. На оси |
них находим угол j |
|
||||
абсцисс (действительная ось) будем откладывать |
4. Записываем комплексное число z в тригонометрической форме. |
|||||
действительную часть комплексного числа, а на оси |
операции над комплексными числами. |
|
||||
ординат (мнимая ось) – мнимую часть. Таким образом, мы |
Сложение комплексных чисел осуществляется в алгебраической |
|||||
построим взаимнооднозначное соответствие между всеми |
||||||
|
|
|||||
комплексными числами и всеми точками плоскости. Если |
форме и определяется следующим образом: суммой |
|||||
такое соответствие построено, то координатная плоскость |
||||||
|
|
|||||
называется комплексной плоскостью. |
|
чисел |
является число |
|||
|
|
|
|
Вычитаное. |
|
|
|
|
|
|
Умножение: |
|
|
Очень важной является интерпретация комплексного |
|
|
||||
числа z = a + ib как вектора OP на комплексной плоскости |
|
|
||||
с началом в точке O (0; 0) и концом в точке P с |
|
|
||||
координатами (a; |
|
|
|
|
||
b). Ясно, что это соответствие является |
|
Деление: |
|
|||
взаимнооднозначным: любому комплексному числу z = a |
|
|
||||
+ ib соответствует вектор и наоборот, каждому вектору |
|
|
||||
соответствует, и притом единственное, число z = a + ib. |
|
|
||||
Модулем комплексного числа называется длина вектора |
|
|
||||
OP, изображающего комплексное число на координатной |
|
|
||||
(комплексной) плоскости. Модуль комплексного числа a+ |
|
|
||||
bi обозначается |a+ bi| или буквой r и равен: Сопряжённые |
Возведение в степень: |
|
||||
комплексные числа имеют одинаковый модуль. |
|
|||||
|
|
|||||
Аргумент комплексного числа - это угол между осью |
|
|
||||
|
|
|
|
Извлечение корня из комплексного числа |
||

7. Показательная форма записи комплексного числа и |
8. Дифференциальные уравнения первого |
||
действия над ними. Формулы Эйлера. |
порядка. Задача Коши для |
||
Показательной формой комплексного числа называется |
дифференциальных уравнений 1-го порядка. |
||
выражение |
— модуль |
Уравнение вида |
|
|
|
||
комплексного числа, |
— расширение экспоненты на случай, |
|
|
когда показатель степени является комплексным числом. |
называется обыкновенным дифференциальным |
||
|
|
уравнением первого порядка. Рассмотрим способы |
|
|
|
решения некоторых его типов. |
|
|
|
Для уравнений вида |
|
|
|
с заданными граничными условиями доказана теорема |
|
|
|
существования и единственности. |
|
|
|
Пусть в области D плоскости (x, y) функция f (x, y) и ее |
|
|
|
частная производная |
непрерывны. Тогда через |
|
|
каждую точку (x0; y0) этой области проходит одна и |
|
|
|
только одна интегральная кривая. |
|
|
|
Задача Коши |
|
|
|
Если, кроме дифференциального уравнения, задано |
|
|
|
также начальное условие в форме y(x0) = y0, то такая |
|
|
|
задача называется задачей Коши. |
|
|
|
Теорема существования и единственности решения |
|
|
|
задачи Коши: если в уравнении y’ = f (x; y) функция f |
|
|
|
(x; y) и ее частная производная f ’y (x; y) непрерывны в |
|
|
|
некоторой области D, содержащей точку (x0; y0), то |
|
|
|
существует единственное решение y = φ (x) этого |
|
|
|
уравнения, удовлетворяющее начальному условию y |
|
|
|
(x0) = y0 или y | x = x0 = y0. |
|
9. Дифференциальные уравнения с разделенными и с |
10. Задачи, приводящие к дифференциальным |
разделяющимися переменными. |
уравнениям. |
Наиболее простым ДУ первого порядка является уравнение вида |
Математические модели в виде уравнений, |
P (x) · dx + Q (y) · dy = 0. |
связывающих независимую переменную, искомую |
В нем одно слагаемое зависит только от x, а другое – от y. Иногда |
функцию и ее производные, называются |
такие ДУ называют уравнениями с разделенными переменными. |
дифференциальными. Решением дифференциального |
Проинтегрировав почленно это уравнение, получаем: |
уравнения называется функция, которая при |
∫ P (x) · dx + ∫ Q (y) · dy = c – его общий интеграл. |
подстановке в уравнение обращает его в тождество. |
Более общий случай описывают уравнения с разделяющимися |
Если искомая (неизвестная) функция зависит от одной |
переменными, которые имеют вид: P1 (x) · Q1 (y) · dx + P2 (x) · Q2 |
переменной, то ДУ называют обыкновенным; в |
(y) · dy = 0. Особенность этого уравнения в том, что коэффициенты |
противном случае – ДУ в частных производных. |
при dx и dy представляют собой произведения двух функций |
Процесс отыскания решения ДУ называется его |
(чисел), одна из которых зависит только от x, другая – только от y. |
интегрированием, а график решения ДУ – интегральной |
|
кривой. |
|
Задачи, приводящие к обыкновенным ДУ: |
|
1) Закон изменения массы радия в зависимости от |
|
времени («радиоактивный распад») описывается |
|
дифференциальным уравнением dm/dt = – k · m, где k > |
|
0 – коэффициент пропорциональности, m (t) – масса |
|
радия в момент t; |
|
2) Зависимость массы x вещества, вступившего в |
|
химическую реакцию, от времени t во многих случаях |
|
описывается уравнением dx/dt = k · x, где k – |
|
коэффициент пропорциональности; |
|
3) «Закон охлаждения тел», т.е. закон изменения |
|
температуры тела в зависимости от времени, |
|
описывается уравнением |
|
dT/dt = k (T – t0), где T (t) – температура тела в момент |
|
времени t, k – коэффициент пропорциональности, t0 – |
|
температура воздуха (среды охлаждения). |

11. Однородные дифференциальные уравнения, |
12. Линейные дифференциальные уравнения 1-го |
однородные функции. |
порядка. |
К уравнению с разделяющимися переменными приводятся |
Дифференциальное уравнение первого порядка называется |
однородные ДУ первого порядка. |
линейным, если его можно записать в виде y’ + p (x) · y = g (x), |
Дифференциальное уравнение y’ = f (x; y) называется |
где p (x) и g (x) – заданные функции, в частности – постоянные. |
однородным, если функция f (x; y) есть однородная функция |
Особенность этого ДУ: искомая функция y и ее производная y’ |
нулевого порядка. |
входят в уравнение в первой степени, не перемножаясь между |
Функция f (x; y) называется однородной функцией n-го |
собой. |
порядка (измерения), если при умножении каждого ее |
|
аргумента на произвольный множитель λ вся функция |
|
умножится на λn, т.е. |
|
f (λ · x; λ · y) = λn · f (x; y). |
|
Однородное ДУ можно записать в виде y’ = φ (y/x). |
|
Однородное уравнение часто задается в дифференциальной |
|
форме: P (x; y) · dx + Q (x; y) · dy = 0. |
|
ДУ будет однородным, если P (x; y) и Q (x; y) – однородные |
|
функции одинакового порядка. |
|
13. Метод вариации произвольной постоянной. |
14. Уравнение Бернулли. |
|
Рассмотрим ЛНДУ y” + α1 (x) y’ + α2 (x) y = f (x). Его общим |
Уравнение вида y’ + p (x) · y = g (x) · yn, n Э IR, n ≠ 0, n ≠ 1 |
|
решением является функция y = y* + . Частное решение y* |
называется уравнением Бернулли. Если n = 0, то это ДУ – |
|
уравнения y” + α1 (x) y’ + α2 (x) y = f (x) можно найти, если |
линейное, а при n = 1 – с разделяющимися переменными. |
|
известно общее решение соответствующего однородного |
На практике ДУ удобнее искать методом И. Бернулли в виде |
|
уравнения y” + α1 (x) y’ + α2 (x) y = 0, методом вариации |
y = u · υ (не сводя его к линейному). |
|
|
||
произвольных постоянных (метод Лагранжа), состоящим в |
|
|
следующем. Пусть = c1y1 (x) + c2y2 (x) – общее решение |
|
|
уравнения y” + α1 (x) y’ + α2 (x) y = 0. Заменим в общем решении |
|
|
постоянные c1 и c2 неизвестными функциями c1 (x) и c2 (x) и |
|
|
подберем их так, чтобы функция y* = c1 (x) • y1 (x) + c2 (x) • y2 (x) |
|
|
была решением уравнения y” + α1 (x) y’ + α2 (x) y = f (x). Найдем |
|
|
производную: (y*)’ = c’1 (x) y1 (x) + c1 (x) y’1 (x) + c’2 (x) y2 (x) + c2 |
|
|
(x) y’2 (x). |
|
|
Подберем функции c1 (x) и c2 (x) так, чтобы |
|
|
c’1 (x) • y1 (x) + c’2 (x) • y2 (x) = 0. |
|
|
Тогда (y*)’ = c1 (x) • y’1 (x) + c2 (x) • y’2 (x), |
|
|
(y*)” = c’1 (x) • y’1 (x) + c1 (x) • y”1 (x) + c’2 (x) • y’2 (x) + c2 (x) • y”2 |
|
|
(x). Подставляя выражение для y*, (y*)’ и (y*)” в уравнение y” + |
|
|
α1 (x) y’ + α2 (x) y = f (x), получим: |
|
|
c’1 (x) • y’1 (x) + c1 (x) • y”1 (x) + c’2 (x) • y’2 (x) + c2 (x) • y”2 (x) + |
|
|
α1 (x) [c1 (x) y’1 (x) + c2 (x) y’2 (x)] + α2 (x) [c1 (x) y1 (x) + c2 (x) y2 |
|
|
(x)] = f (x). Поскольку y1 (x) и y2 (x) – решения уравнения y” + α1 |
|
|
(x) y’ + α2 (x) y = 0, то выражения в квадратных скобках равны |
|
|
нулю, а потому c’1 (x) • y’1 (x) + c’2 (x) • y’2 (x) = f (x). |
|
|
Таким образом, функция y* = c1 (x) • y1 (x) + c2 (x) • y2 (x) будет |
|
|
частным решением y* уравнения y” + α1 (x) y’ + α2 (x) y = f (x), |
|
|
если функции c1 (x) и c2 (x) удовлетворяют системе уравнений: |
|
|
{c’1 (x) • y1 (x) + c’2 (x) • y2 (x) = 0, |
(1) |
|
{c’1 (x) • y’1 (x) + c’2 (x) • y’2 (x) = f (x). |
|
|
Определитель системы | y1 (x) y2 (x) |
| ≠ 0, т.к. это |
|
определитель |
|
|
| y’1 (x) y’2 (x) | |
|
|
Вронского для фундаментальной системы частных решений y1 |
|
|
(x) и y2 (x) уравнения y” + α1 (x) y’ + α2 (x) y = 0. Поэтому система |
|
|
(1) имеет единственное решение: c’1 (x) = φ1 (x) и c’2 (x) = φ2 (x), |
|
|
где φ1 (x) и φ2 (x) – некоторые функции от x. Интегрируя эти |
|
|
функции, находим c1 (x) и c2 (x), а затем по формуле y* = c1 (x) • |
|
|
y1 (x) + c2 (x) • y2 (x) составляем частное решение уравнения |
|
|
y” + α1 (x) y’ + α2 (x) y = f (x). |
|
|

15. Дифференциальные уравнения высших порядков. |
16. Основные виды дифференциальных уравнений |
Задача Коши для дифференциальных уравнений |
высших порядков и их решение. |
высших порядков. |
|
Дифференциальные уравнения порядка выше первого |
|
называются ДУ высших порядков. ДУ второго порядка в общем |
|
случае записывается в виде F (x; y; y’; y”) = 0 или, если это |
|
возможно, в виде, разрешенном относительно старшей |
|
производной: y” = f (x; y; y’). |
|
Решением последнего ДУ называется всякая функция y = φ (x), |
|
которая при подстановке в уравнение обращает его в |
|
тождество. |
|
Общим решением ДУ называется функция y = φ (x; c1; c2), где c1 |
|
и c2 – не зависящие от x произвольные постоянные, |
|
удовлетворяющая условиям: |
|
1.φ (x; c1; c2) является решением ДУ для каждого фиксированного значения c1 и c2 .
2.Каковы бы ни были начальные условия y | x = x0 = y0, y’ | x = x0 = y’0, существуют единственные значения постоянных c1 = c10 и c2 = c20 такие, что функция y = φ (x; c10; c20) является решением уравнения y” = f (x; y; y’) и удовлетворяет начальным условиям.
Всякое решение y = φ (x; c10; c20) уравнения y” = f (x; y; y’),
получающееся из общего решения y = φ (x; c1; c2) при конкретных значениям постоянных c1 = c10, c2 = c20, называется частным решением.
Как и в случае уравнения первого порядка, задача нахождения решения ДУ y” = f (x; y; y’), удовлетворяющего заданным начальным условиям y | x = x0 = y0, y’ | x = x0 = y’0, называется задачей Коши.
Теорема существования и единственности задачи Коши: если в уравнении y” = f (x; y; y’) функция f (x; y; y’) и ее частные производные f ’y и f ‘y’ непрерывны в некоторой области D изменения переменных x, y и y’, то для всякой точки (x0; y0; y’0) Э D существует единственное решение y = φ (x) уравнения y” = f (x; y; y’), удовлетворяющее начальным условиям y | x = x0 = y0, y’ | x = x0 = y’0 .
Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменной (подстановки) данное ДУ сводится к уравнению, порядок которого ниже.
3типа уравнений, допускающих понижение порядка: 1) y” = f (x);
2) y” = f (x; y’), не содержащее явно искомой функции y. Частный случай: y” = f (y’), не содержащее также и независимую переменную x.
3) y” = f (y; y’), которое не содержит явно независимой переменной x.
Частный случай: y” = f (y).
17. Система линейно-независимых функций. |
18. Линейные дифференциальные уравнения n-го |
|
Определитель Вронского. |
порядка. |
|
Функции y1, y2 , … , yn называются линейно независимыми на |
Уравнение вида b0 (x) y(n) + b1 (x) y(n – 1) + … + bn (x) y = g (x), |
|
(a; b), если равенство α1y1 + α2y2 + … + αnyn = 0 выполняется |
где b0 (x) ≠ 0, b1 (x), … , bn (x), g (x) – заданные функции (от x), |
|
лишь в случае, когда все числа αi = 0 (I = 1, 2, … , n); в противном |
называются линейным ДУ n-го порядка. |
|
случае (если хотя бы одно из чисел αi не равно нулю) функции |
Если свободный член g (x) 0, то это уравнение называется |
|
y1, y2 , … , yn – линейно зависимы. |
линейным однородным уравнением; если g (x) ≠ 0, то уравнение |
|
b0 (x) y(n) + b1 (x) y(n – 1) + … + bn (x) y = g (x) называется |
||
Функции y1 = y1 (x) и y2 = y2 (x) называются линейно |
||
неоднородным. |
||
независимыми на интервале (a; b), если равенство |
||
Линейные однородные дифференциальные уравнения n-го |
||
α1y1 + α2y2 = 0, где α1 , α2 Э IR, выполняется тогда и только |
||
порядка имеют вид y(n) + a1 (x) • y(n – 1) + a2 (x) • y(n – 2) + … |
||
тогда, когда α1 = α2 = 0. Если хотя бы одно из чисел α1 или α2 |
||
+ an (x) • y = 0. |
||
отлично от нуля и выполняется равенство α1y1 + α2y2 = 0, то |
||
Если функции y1 = y1 (x), y2 = y2 (x), … , yn = yn (x) являются |
||
функции y1 и y2 называются линейно зависимыми на (a; b). |
||
частными решениями этого уравнения, то его решением |
||
Определитель Вронского имеет вид: |
||
является функция y = c1y1 + c2y2 + … + cnyn . |
||
|

19. Линейные дифференциальные уравнения 2-го
порядка с постоянными коэффициентами.
Частным случаем линейных однородных дифференциальных уравнений являются ЛОДУ n-го порядка (n>2) с постоянными коэффициентами: y(n)
1) + p2y(n – 2) + … + pny = 0, где pi ,
i = 1, , - числа.
Частные решения этого уравнения ищем в виде y = ekx, где k – постоянное число.
Характеристическим для уравнения y(n) + p1y(n – 1) + p2y(n – 2) + … + pny = 0 является алгебраическое уравнение n-го порядка вида
kn + p1kn – 1 p2kn – 2 + … + pn – 1 k + pn = 0.
Это уравнение имеет, как известно, n корней (в их числе могут быть и комплексные). Обозначим их через k1 , k2 , …
, kn .
Замечание: не все из корней уравнения kn + p1kn – 1 p2kn – 2 + … + pn – 1 k + pn = 0 обязаны быть различными. Так, в частности, уравнение (k – 3)2 = 0 имеет два равных корня: k1 = k2 = 3. В этом случае говорят, что корень один (k = 3) и имеет кратность mk = 2. Если кратность корня равна единице: mk = 1, его называют простым.
Случай 1: все корни уравнения kn + p1kn – 1 p2kn – 2 + … + pn – 1 k + pn = 0 действительны и просты (различны). Тогда функции y1 = ek1x, y2 = ek2x, … , yn = eknx, являются частными решениями уравнения y(n) + p1y(n – 1) + p2y(n – 2) + … + pny = 0 и образуют фундаментальную систему решений (линейно независимы). Поэтому общее решение
уравнения y(n) + p1y(n – 1) + p2y(n – 2) + … + pny = 0
записывается в виде
y = c1ek1x + c2ek2x + … + cneknx.
20.Линейные дифференциальные уравнения с постоянными коэффициентами с правой частью
специального вида.
Рассмотрим ЛНДУ второго порядка с постоянными коэффициентами, т.е. уравнение y” + p · y’ + q · y = f (x), где p и q – некоторые числа.
Согласно теореме о структуре общего решения ЛНДУ, общее решение этого уравнения представляет собой сумму общего решения ̂ соответствующего однородного уравнения и частного решения y* неоднородного уравнения. Частное решение уравнения может быть найдено методом вариации произвольных постоянных.
Для уравнений с постоянными коэффициентами существует более простой способ нахождения y*, если правая часть f (x) уравнения y” + p · y’ + q · y = f (x) имеет так называемый «специальный вид»:
I. f (x) = Pn (x) · eαx или II. f (x) = eαx · (Pn (x) · cos βx + Qm (x) · sin βx).
Суть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части f (x) уравнения y” + p · y’ + q · y = f (x) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют ее в уравнение y” + p · y’ + q · y = f (x) и из полученного тождества находят значения коэффициентов.
21. Метод вариации произвольных постоянных. |
22. Функции нескольких переменных. Метод сечения в |
|||
Рассмотрим ЛНДУ y” + α1 (x) y’ + α2 (x) y = f (x). Его общим |
построении графика. |
|||
решением является функция y = y* + ̂. Частное решение y* |
|
|
||
уравнения y” + α1 (x) y’ + α2 (x) y = f (x) можно найти, если |
|
|
||
известно общее решение ̂ соответствующего однородного |
|
|
||
уравнения y” + α1 (x) y’ + α2 (x) y = 0, методом вариации |
|
|
||
произвольных постоянных (метод Лагранжа), состоящим в |
|
|
||
следующем. Пусть ̂ = c1y1 (x) + c2y2 (x) – общее решение |
|
|
||
уравнения y” + α1 (x) y’ + α2 (x) y = 0. Заменим в общем решении |
|
|
||
постоянные c1 и c2 неизвестными функциями c1 (x) и c2 (x) и |
|
|
||
подберем их так, чтобы функция y* = c1 (x) · y1 (x) + c2 (x) · y2 (x) |
|
|
||
была решением уравнения y” + α1 (x) y’ + α2 (x) y = f (x). Найдем |
|
|
||
производную: (y*)’ = c’1 (x) y1 (x) + c1 (x) y’1 (x) + c’2 (x) y2 (x) + c2 |
|
|
||
(x) y’2 (x). |
|
|
|
|
Подберем функции c1 (x) и c2 (x) так, чтобы |
|
|
||
c’1 (x) · y1 (x) + c’2 (x) · y2 (x) = 0. |
|
|
|
|
Тогда (y*)’ = c1 (x) · y’1 (x) + c2 (x) · y’2 (x), |
|
|
||
(y*)” = c’1 (x) · y’1 (x) + c1 (x) · y”1 (x) + c’2 (x) · y’2 (x) + c2 (x) · y”2 |
|
|
||
(x). Подставляя выражение для y*, (y*)’ и (y*)” в уравнение y” + α1 |
|
|
||
(x) y’ + α2 (x) y = f (x), получим: |
|
|
|
|
c’1 (x) · y’1 (x) + c1 (x) · y”1 (x) + c’2 (x) · y’2 (x) + c2 (x) · y”2 (x) + α1 |
|
|
||
(x) [c1 (x) y’1 (x) + c2 (x) y’2 (x)] + α2 (x) [c1 (x) y1 (x) + c2 (x) y2 (x)] = |
|
|
||
f (x). Поскольку y1 (x) и y2 (x) – решения уравнения y” + α1 (x) y’ + |
|
|
||
α2 (x) y = 0, то выражения в квадратных скобках равны нулю, а |
|
|
||
потому c’1 (x) · y’1 (x) + c’2 (x) · y’2 (x) = f (x). |
|
|
||
Таким образом, функция y* = c1 (x) · y1 (x) + c2 (x) · y2 (x) будет |
|
|
||
частным решением y* уравнения y” + α1 (x) y’ + α2 (x) y = f (x), |
|
|
||
если функции c1 (x) и c2 (x) удовлетворяют системе уравнений: |
|
|
||
{c’1 (x) · y1 (x) + c’2 (x) · y2 (x) = 0, |
(1) |
|
|
|
{c’1 (x) · y’1 (x) + c’2 (x) · y’2 (x) = f (x). |
|
|
|
|
Определитель системы | y1 (x) |
y2 (x) |
| ≠ 0, т.к. это определитель |
|
|
| y’1 (x) |
y’2 (x) | |
|
|
|
Вронского для фундаментальной системы частных решений y1 (x) |
|
|
||
и y2 (x) уравнения y” + α1 (x) y’ + α2 (x) y = 0. Поэтому система (1) |
|
|
||
имеет единственное решение: c’1 (x) = φ1 (x) и c’2 (x) = φ2 (x), где |
|
|
||
φ1 (x) и φ2 (x) – некоторые функции от x. Интегрируя эти функции, |
|
|
||
находим c1 (x) и c2 (x), а затем по формуле y* = c1 (x) · y1 (x) + c2 |
|
|
||
(x) · y2 (x) составляем частное решение уравнения |
|
|
||
y” + α1 (x) y’ + α2 (x) y = f (x). |
|
|
|
|
|
|
|
|
|

23.Системы дифференциальных уравнений. (Каноническая и однородная системы).
Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.
Общий вид системы ДУ первого порядка, содержащей n искомых функций y1, y2, … , yn, следующий:
{F1 (x ; y1 ; y2 ; … ; yn ; y’1 ; y’2 ; … ; y’n ) = 0,
{……………………………………………….
{Fn (x ; y1 ; y2 ; … ; yn ; y’1 ; y’2 ; … ; y’n ) = 0.
Система ДУ первого порядка, разрешенных относительно производной, т.е. система вида
{dy1/dx = f1 (x ; y1 ; y2 ; … ; yn ),
{dy2/dx = f2 (x ; y1 ; y2 ; … ; yn ), (1)
{…………………………………
{dyn/dx = fn (x ; y1 ; y2 ; … ; yn ),
Называется нормальной системой ДУ. При этом предполагается, что число уравнений равно числу искомых функций.
Замечание: во многих случая системы уравнений и уравнения высших порядков можно привести к нормальной системе вида
(1).
Решением системы (1) называется совокупность из n функций y1, y2, … , yn, удовлетворяющих каждому из уравнений этой системы.
Начальные условия для системы (1) имеют вид: y1 (x0) = y01, y2 (x0) = y02, … , yn (x0) = y0n .
Задача Коши для системы (1) ставится следующим образом: найти решение системы (1), удовлетворяющее начальным условиям y1 (x0) = y01, y2 (x0) = y02, … , yn (x0) = y0n .
Условия существования и единственности решения задачи Коши описывает следующая теорема: если в системе (1) все функции fi (x ; y1 ; … , yn ) непрерывны вместе со всеми своими частными производными по yi в некоторой области D ((n + 1)- мерного пространства), то в каждой точке M0 (x0 ; y01 ; y02 ; … ; y0n ) этой области существует, и притом единственное, решение y1 = φ1 (x), y2 = φ2 (x), … , yn = φn (x) системы, удовлетворяющее начальным условиям y1 (x0) = y01, y2 (x0) = y02, … , yn (x0) = y0n .
Линейные системы ДУ имеют вид:
dx1/dt = a11 (t) x1 + a12 (t) x2 + … + a1n (t) xn + f1 (t) } dx2/dt = a21 (t) x1 + a22 (t) x2 + … + a2n (t) xn + f2 (t) } (1)
…………………………………………………….. } dxn/dt = an1 (t) x1 + an2 (t) x2 + … + ann (t) xn + fn (t) }
где fi (t) – некоторые функции.
dxi/dt = ∑=1 ij (t) xj + fi (t), где i = 1,2, … , n.
dX/dt = A · X + F |
|
|
|
|
(dx1/dt) |
(x1 ) |
(a11 a12 … a1n) |
(f1 |
(t) ) |
dX/dt = (dx2/dt) , X = (x2 ) , A = (a21 a22 … a2n) , F = (f2 |
(t) ) |
|||
(…….) |
(…) |
(……………) |
(…… ) |
|
(dxn/dt) |
(xn ) |
(an1 an2 … ann) |
(fn (t) ) |
|
Если все функции aij (t) и fi (t) в системе (1) на некотором отрезке a ≤ t ≤ b непрерывны, то в достаточно малой окрестности точки t0 a < t0 < b, координаты которой (t0, x10, x20 , … , xn0), выполняются условия теоремы Коши о существовании и единственности решения задачи Коши.
24. Частные производные и их свойства.
Частная производная ф-ции z f (x, y) в точке P(x0 , y0 )
по переменной x называется
|
lim |
|
f (x0 x, y0 ) f (x0 , y0 ) |
, если он . |
|||||||||||
|
|
|
|||||||||||||
x 0 |
|
|
|
|
x |
|
|
|
|
|
|
||||
|
dz |
| |
|
, Z ' |
|
(P ), |
dt |
| |
, f ' |
|
(x , y |
) ; |
|
||
|
|
|
|
x |
|
x |
|||||||||
|
dy |
p0 |
0 |
dx |
p0 |
0 0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
dz |
lim |
f (x0 , y0 y) f (x0 , y0 ) |
; |
|||||||||||
|
|
|
|||||||||||||
|
dy |
|
y 0 |
|
|
|
y |
|
|
|
|
|
|||
U f (M ) непрерывна U 'x |A ,U 'y |A |
|||||||||||||||
U f (x) |
имеет частные производные в т. А,В f (M ) |
||||||||||||||
непрерывна в т. А,В.
Частные производные обладают теми же свойствами что и обычное производные.

25.Дифференциал функции 2-х переменных. Применение дифференциала в приближенных
вычислениях
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):dy=ƒ'(х)•∆х.
Дифференциал обладает следующими основными свойствами.
1.d(с)=0.
2.d(u+w-v)= du+dw-dv.
3.d(uv)=du·v+u·dv.
d(сu)=сd(u).
4. |
. |
5.y=f(z),  ,
,  ,
,
.
Применение дифференциала в приближенных
вычислениях
Приращение  функции
функции  представимо в виде:
представимо в виде:
где функция  является б.м. функцией при стремлении аргумента
является б.м. функцией при стремлении аргумента  к нулю. Так как
к нулю. Так как  , то
, то
В силу того, что второе слагаемое  является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.
Для приближенного вычисления значения функции применяется следующая формула:
26. Касательная плоскость к поверхности и нормаль.
Определение 1: касательная плоскость к
поверхности в точке  – это плоскость, содержащая касательные ко всем кривым, которые принадлежат
– это плоскость, содержащая касательные ко всем кривым, которые принадлежат
данной поверхности и проходят через точку  .
.
Определение 2: нормаль к поверхности в точке  – это прямая, проходящая через данную точку перпендикулярно касательной плоскости.
– это прямая, проходящая через данную точку перпендикулярно касательной плоскости.
Пусть поверхность задана в неявном виде: F(x,y,z)=0 и пусть точка M0(x0,y0,z0) принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке M0 таково:
Уравнение нормали имеет вид:
Если же уравнение поверхности задано в явном виде z=f(x,y), то уравнение касательной плоскости имеет вид:
Уравнение нормали в случае явного задания поверхности таково:

27.Экстремум функции двух переменных. Необходимые условия существования экстремума.
Понятие максимума и минимума функции двух переменных аналогично этим же понятиям для функции независимой переменной.
Говорят, что функция  имеет максимум в
имеет максимум в
точке  , т.е. при
, т.е. при  ,
,
если  для всех точек
для всех точек  , достаточно близких к точке
, достаточно близких к точке  и отличных от неё. Говорят, что функция
и отличных от неё. Говорят, что функция 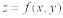 имеет минимум в
имеет минимум в
точке 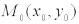 , т.е. при
, т.е. при  ,
,
если  для всех точек
для всех точек  ,
,
достаточно близких к точке  и отличных от неё. Максимум и минимум функции называются экстремумами функции.
и отличных от неё. Максимум и минимум функции называются экстремумами функции.
Если функция z = f(x, y) в точке имеет экстремум, то в этой точке обе частные производные равны нулю (fx¢(P0) = 0, fy¢(P0) = 0) или, по крайней мере, одна из них не существует.
Теорема имеет простой геометрический смысл. Касательная плоскость к поверхности z = f(x, y) в точке экстремума P0 параллельна плоскости Оху (zx¢(P0) = 0, zy¢(P0) = 0) или не существует. Необходимые условия существования экстремума остаются справедливыми и для функций большего числа переменных. Точки, в которых все частные производные первого порядка функции z = f(P) равны нулю или хотя бы одна из них не существует, называются критическими точками. Если в критической точке функция дифференцируема, то все частные производные первого порядка в ней обращаются в нуль. Такую точку часто называют стационарной. Для отыскания стационарных точек функции z = f(x, y) находят частные производные первого порядка и решают систему уравнений
(3)
28.Достаточное условие существования экстремума. Дифференциал второго порядка функции двух переменных.
Пусть функция z = f(x,y) в стационарной точке Р0 (х0,у0) имеет непрерывные частные производные до третьего порядка включительно. Если А = f¢¢xx (Р0), B = f¢¢xy (Р0), C = f¢¢yy (Р0)
и D(Р0) = АС - В2, то возможны три случая:
1)при D(Р0) > 0 Р0 – точка экстремума, причем, в точке Р0 максимум, когда А < 0, и минимум, когда А > 0;
2)при D(Р0) < 0 Р0 не является точкой экстремума;
3)при D(Р0) = 0 о характере стационарной точки Р0 никакого заключения сделать нельзя, нужны дополнительные исследования.
Замечание. Приведенные выше условия эквивалентны следующим. Пусть Р0 – стационарная точка функции z = f(x, y), т.
е. d f(Р0) = 0, тогда:
1)если d2f(Р0) < 0 при dx2 + dy2 ¹ 0, то f(Р0) – максимум функции f(x, y);
2)если d2 f(Р0) > 0 при dx2 + dy2 ¹ 0, то f(Р0) – минимум функции f(x, y);
3)если d2f(Р0) меняет знак, то f(Р0) не является экстремумом. Дифференциал от первого дифференциала функции называется вторым дифференциалом:
Аналогично определяются дифференциалы более старших порядков.
Вычислим второй дифференциал функции двух переменных
 При этом будем считать, что дифференциалы независимых переменных dx и dy – величины постоянные (т.е. не зависят от т.(х,у) и не меняются при вычислении каждого последующего дифференциала).
При этом будем считать, что дифференциалы независимых переменных dx и dy – величины постоянные (т.е. не зависят от т.(х,у) и не меняются при вычислении каждого последующего дифференциала).
Не трудно видеть, что второй дифференциал представляет собой квадратичную форму от
переменных dx и dy. Матрица этой квадратичной формы есть матрица Гессе, т.е.
d2z = (dx,dy)Г(dx,dy)T (см. раздел «Линейная алгебра», квадратичные формы). Кроме того, второй дифференциал можно записать в символическом виде:
 Можно показать, что в общем случае дифференциал 2 – го порядка функции u = F(x) равен
Можно показать, что в общем случае дифференциал 2 – го порядка функции u = F(x) равен
Дифференциал m – го порядка равен

29.Условный экстремум. Функция Лагранжа.
Вэтом методе не требуется выражать явно y через х , однако используется то обстоятельство, что в случае предполагаемой замены y на g(x) дело сводится к безусловному экстремуму функции одной переменной.
dz f f dy dx x y dx
Итак, находим полную прозводную от z по х, считая y функцией х:
f |
|
f dy |
0 |
|
x |
y dx |
|||
|
|
В точках экстремума dz: dx=0, следовательно (1),
Применим снова правило дифференцирования сложной функции к уравнению φ(x,y)=0. Будем предполагать при этом, что у заменен той самой функцией х, которая неявно задается уравнением. Такая замена превращает уравнение φ(x,y)=0 в тождество. Получим (2):
dy
x y dx
0
Умножим (2) на неопределенный множитель λ и сложим с (1):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
f |
|
f |
|
dy |
|
|
|
|
|
|
|
|
dy |
|
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x |
|
y dx |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
y dx |
|
|
||||||||||||||||
|
f |
|
|
|
|
|
|
|
f |
|
|
dy |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0(3) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
y dx |
|
||||||||||||
Мы будем предполагать, что в точке экстремума у . Тогда
существует число , при котором f y + ( у) = 0 в этой точке. Из равенства (3) следует, что в этой точке f х + ( х) = 0
|
f |
|
|
0 |
|
|
|
|
|||
x |
x |
||||
|
|
|
|||
|
f |
|
|
0 |
|
|
|
|
|||
y |
y |
||||
|
|
|
|||
|
(x, y) 0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Мы приходим к необходимым условиям экстремума (4):
В этой системе из трех уранений три неизвестные величины x, y и . Из системы находятся одна или несколько точек (х,у). Что касается , то этот множитель играет вспомогательную роль и дальше не требуется. Найденные точки (х,у) проверяют на наличие в них экстремума и его вид (максимум или минимум). В случае необходимости вычисляются значения f(x,y) на концах промежутка, ограничивающего изменение х при описании кривой АВ. Часто из существа задачи легко решается вопрос, с каким из значений - наибольшим или наименьшим - мы имеем дело. Проведенные рассуждения обосновывают метод Лагранжа, который состоит в следующем.
Составляется вспомогательная функция
F (x,y, ) = f(x,y) + (x,y) (5), называемая функцией Лагранжа. Для нее выписываются как для функции трех переменных необходимые условия абсолютного экстремума:
F'x 0, F'y 0, F' 0.
При этом получается в точности система (4). Коэффициент называют множителем Лагранжа.
Метод Лагранжа допускает обобщение на функции большего числа переменных. Так, в задаче на условный экстремум функции u=f(x,y,z)
30.Наибольшее/наименьшее значение функции на ограниченной области.
Итак, для того, чтобы найти наибольшее и наименьшее значения функции z = f (х, у), непрерывной в
ограниченной замкнутой области  , необходимо воспользоваться следующим правилом:
, необходимо воспользоваться следующим правилом:
1. Найти критические точки данной функции,
лежащие в области  и вычислить значения функции в этих точках (не классифицируя экстремума).
и вычислить значения функции в этих точках (не классифицируя экстремума).
2.Найти наибольшее и наименьшее значения функции на линиях, образующих границу области.
3.Из всех полученных значений выбрать наибольшее и наименьшее.
Заметим, что подобным же образом решается задача об отыскании наименьшего и наибольшего значений
функции трёх переменных u = f (х, у, z), в замкнутой трёхмерной области.
