
math-st796 / Дифференциальные уравнения в задачах и примерах_Пушкарь Е.А_Уч-метод. пос_МГИУ, 2007 -158с
.pdf
Критерий устойчивости по первому приближению |
131 |
|
|
Следовательно, положение равновесия x = −1, y = −1 также неустойчиво.
Задача 24.2. |
Исследовать устойчивость решения x = 0, |
|||||||||||
y = 0, z = 0 системы уравнений |
|
|
|
|
|
|
||||||
dydt |
= sin2 |
(x |
|
z) |
|
|
y |
|
sin z, |
|||
dxdt |
= − sin (x − z), |
|
|
|
|
|
||||||
dz |
− |
|
|
|
|
− |
|
− |
|
− |
|
|
|
= tg (y |
− |
z). |
|
|
|
|
|
|
|||
dt |
|
|
|
|
|
|
|
|
|
|
||
Решение: Уравнения первого приближения, соответству- |
||||||||||||
ющие данной системе, имеют вид |
|
|
|
|
|
|||||||
|
dy |
|
|
− − |
|
|
|
|
||||
|
|
dx |
= |
|
x |
|
z, |
|
|
|||
|
dt |
|
|
− − |
|
|
|
|
||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
= |
|
y |
|
z, |
|
(24.2) |
||
|
|
|
|
|
|
|||||||
dt = y − z.
Собственные числа матрицы коэффициентов системы уравнений (24.2) определяются из характеристического уравнения
−10− λ |
|
10 |
λ |
−1 |
= 0 |
или (λ + 1)(λ2 + 2λ + 2) = 0. |
|
|
0 |
− |
1− |
|
1 |
λ |
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− − |
|
|
|
|
|
|
|
|
|
|
|
Корни характеристического |
уравнения – действительный |
|||||
λ1 = −1 и комплексные λ2,3 = −1 ± i, – имеют отрицательные вещественные части. Следовательно, нулевое решение x = 0, y = 0, z = 0 данной системы уравнений асимптотически устойчиво.
Задача 24.3. Найти все положения равновесия системы
уравнений |
|
|
|
||
|
dx |
|
|
|
|
|
|
= x2 + y2 |
|
17. |
|
dy |
|
||||
dt |
= xy + 4, |
|
(24.3) |
||
|
|
|
|
||
dt |
|
− |
|
||
|
|
|
|
|
|
132 |
24 Практическое занятие |
|
|
Исследовать иx устойчивость и определить типы особых то-
чек.
Решение: Положения равновесия (особые точки) данной системы определяются из системы уравнений
xy + 4 = 0,
x2 + y2 − 17 = 0.
Решая эти уравнения, находим четыре положения равновесия: A(−1; 4), B(−4; 1), C(1; −4) и D(4; −1).
Раскладывая правые части исходной системы в ряд Тейлора
вокрестности положения равновесия (x0, y0) и ограничиваясь
вэтих разложениях линейными членами, получим уравнения первого приближения
|
|
dy |
= 2x0(x− x0) + 2y0(y y0). |
|
|
|||||||||
|
|
dxdt |
= y0(x x0) + x0 |
(y − y0), |
|
|
||||||||
|
|
dt |
|
|
|
− |
|
|
|
− |
|
|
|
|
Заменяя x − x0 на x, а y − y0 на y, имеем |
|
|
||||||||||||
|
|
|
|
|
dydt |
= 2x0x + 2y0y. |
|
|
|
|
||||
|
|
|
|
|
|
dx |
= y |
x + x y, |
|
|
|
|
||
|
|
|
|
|
|
dt |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составляем характеристическое уравнение |
− |
|
||||||||||||
|
2x0 |
2y0 |
|
|
λ |
|
|
|
− |
|
|
0 |
0 |
|
|
y0 − λ |
x0 |
|
|
= 0, |
λ2 |
|
3y0λ + 2(y2 |
x2) = 0. |
|||||
|
|
− |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если y02 < x20, то корни характеристического уравнения действительны и имеют разные знаки. Так как координаты положений равновесия B и D удовлетворяют этому условию, то указанные положения равновесия неустойчивы. Особые точки (−4; 1) и (4; −1) являются особыми точками типа “седло”.
Характеристические уравнения, соответствующие точкам A и C, имеют вид
λ2 − 12λ + 30 = 0 и λ2 + 12λ + 30 = 0.

Критерий устойчивости по первому приближению |
133 |
|
|
Оба корня первого из них положительны, а второго – отрицательны. Поэтому положение равновесия A(−1; 4) неустойчиво, а положение C(1; −4) асимптотически устойчиво.
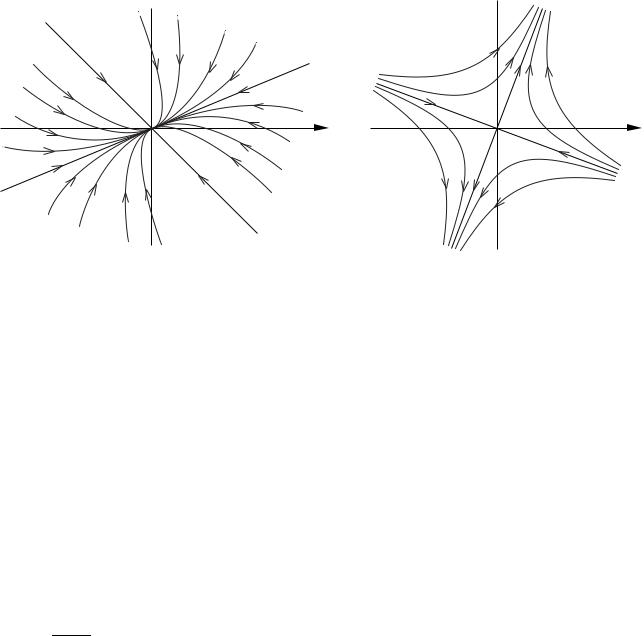
Особая точка A является неустойчивым узлом, а точка C – устойчивым узлом. Поведение траекторий в окрестности положений равновесия изображено на рис. 24.1.
Рис. 24.1. Траектории решений системы (24.3)
Задача 24.4. Исследовать устойчивость всех особых точек системы уравнений
dt |
= x2 |
− y2 |
− 5, |
(24.4) |
|||
|
dx |
+ y2 |
|
13. |
|
||
dy |
= x2 |
|
|
||||
|
|
|
|
|
|
|
|
dt |
|
|
− |
|
|
||
|
|
|
|
|
|
|
|
Определить типы особых точек.
Решение: Особые точки (положения равновесия) данной системы определяем из системы алгебраических уравнений
x2 − y2 − 5 = 0, x2 + y2 − 13 = 0.

134 |
24 Практическое занятие |
|
|
Отсюда находим четыре особые точки: A(−3; −2), B(−3; 2), C(3; 2), D(3; −2). Система первого приближения, соответствующая исходной системе, в окрестности особой точки (x0; y0) имеет вид
dxdt = 2x0(x − x0) − 2y0(y − y0), dydt = 2x0(x − x0) + 2y0(y − y0),
откуда, заменяя (x − x0) на x и y − y0 на y, получим
dxdt = 2x0x − y0y, dydt = 2x0x + 2y0y.
Собственные числа матрицы коэффициентов этой системы определяются из уравнения
λ2 − 2(x0 + y0)λ + 8x0y0 = 0. |
(24.5) |
Если x0y0 < 0, то уравнение (24.5) имеет действительные корни разных знаков. Неравенство x0y0 < 0 выполняется для особых точек B и D. Таким образом, эти точки неустойчивы и являются особыми точками типа “седло”.
 y
y
B |
C |
0 |
x |
A |
|
|
D |
Рис. 24.2. Траектории решений системы (24.4)



Особые точки на фазовой плоскости |
137 |
|
|
Сделать схематический чертеж.
Решение: Составим и решим характеристическое уравнение:
|
−31− λ |
42 |
λ |
|
= 0, λ2 + 7λ + 10 = 0, λ1 = −2, λ2 = −5. |
|
|
|
− − |
|
|
|
|
|
|
|
|
|
|
|
|
Корни |
характеристического |
уравнения действительные и |
|||
отрицательные; следовательно, положение равновесия – устойчивый узел.
Прямые, содержащие фазовые кривые системы, ищем в виде
y = kx. Подставляя y = kx в уравнение |
|
|
|
|
||||||||
|
|
|
|
dy |
= |
x − 4y |
, |
|
|
|
|
|
|
|
|
|
|
−3x + 2y |
|
|
|
|
|||
|
|
|
|
dx |
|
|
|
|
|
|
||
получаем уравнение для определения k: |
|
|
|
|
||||||||
k = |
1 − 4k |
, |
2k2 + k |
− |
1 = 0, |
k = 1, |
k = |
1 |
. |
|||
|
2 |
|||||||||||
|
3 + 2k |
|
|
|
|
1 |
− |
2 |
|
|||
|
− |
|
|
|
|
|
|
|
|
|
|
|
Значит, y = −x и y = x/2 – искомые прямые. Остальные фазовые кривые – части парабол, касающихся в начале координат прямой y = x/2. Их схематически можно построить, например, методом изоклин. То, что эти параболы касаются именно прямой y = x/2, следует из того, что собственный вектор {2; 1} матрицы коэффициентов данной системы, соответствующий собственному значению λ1 = −2 (меньшему по модулю), параллелен прямой y = x/2 (фазовые кривые изображены на рис. 25.2 (a)).
Задача 25.3. Определить тип положения равновесия си-
стемы уравнений
dx
dt = 2y,
dy = 2x + 3y
dt
и исследовать поведение фазовых кривых.


140 |
26 Практическое занятие |
|
|
Движение фазовой точки по этим спиралям происходит в направлении к положению равновесия, если α < 0, и от него, если α < 0 (рис. 25.3). Направление движения найдем, вычислив направляющий вектор (x,˙ y˙) в какой-нибудь точке. Например, задав x = 1, y = 0, находим, что направляющий вектор в точке (1, 0) равен (α, −1 + α), т.е. при малых α движение происходит по часовой стрелке, как показано на рис. 25.3.
Задачи для самостоятельного решения
Исследовать поведение фазовых кривых систем уравнений:
1. |
dt |
= 2x, |
|
|
|
dx |
= x + y. |
|
dy |
||
|
|
|
|
dt
dx
2.dt = −3x + 2y,
dy = x − 4y.
dt
dx
3.dt = 3x − 4y,
dy = x − 2y.
dt
dx
4.dt = −2x − 5y,
dy = 2x + 2y.
dt
dx
5.dt = x − 2y,
dy = 2x − 3y.
dt
dx
6.dt = x − 2y,
dy = 3x + 4y.
dt

 y
y y
y