
ser
.pdf
22
Вычислим значения этих производных при x = 0, принимая во внимание
начальное условие y(0) = |
1 |
|
и данное уравнение y' = x2 + y 2 , откуда |
|||||||||||||||||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y' (0) = 0 |
|
|
|
|
1 |
|
; |
|
|
y' ' (0) = 2 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
; |
|
|
|
|||||||||||||
+ |
|
|
= |
|
|
|
|
|
0 + 2 |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||||||||||||
|
4 |
|
|
|
|
2 |
|
4 |
|
4 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
2 |
|
1 |
|
|
1 |
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y' ' ' (0) = 2 + 2 |
1 |
|
+ 2 |
|
|
|
|
|
= |
; |
y (4) |
(0) = |
1 |
|
|
+ |
1 |
|
+ |
19 |
= |
11 |
. |
|||||||||||||||||||
42 |
|
2 |
|
|
4 |
|
|
|
4 |
|
8 |
|
|
8 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||
Подставляя эти значения в ряд Маклорена, получаем: |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
y(x) = |
1 |
|
+ |
|
1 |
x |
+ |
1 |
x |
2 |
+ |
19 |
|
|
x |
3 |
|
+ |
|
11 |
x |
4 |
+... |
||||||||||||||||
|
|
|
2 |
|
4 |
8 |
|
|
48 |
|
|
|
|
|
96 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
III.РЯДЫ ФУРЬЕ
1.Рядом Фурье функции f (x), определённой на отрезке [–π, π], называется ряд
a0 + ∑∞ (an cos nx + bn sin nx), 2 n=1
коэффициенты которого определяются по формулам
|
|
|
|
|
|
|
1 |
π |
|
|
|
||
|
|
|
a0 = |
∫ f (x) dx , |
|
||||||||
|
|
|
π |
|
|||||||||
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
1 |
|
π |
|
|
|
|
|
|
|
|||
an = |
|
∫ f (x) cos nx dx |
(n =1, 2, ...) , |
|
|||||||||
π |
|
||||||||||||
|
|
|
−π |
|
|
|
|
|
|
|
|||
|
|
1 |
|
π |
|
|
|
|
|
|
|
||
bn = |
|
∫ f (x) sin nx dx |
(n =1, 2, ...) |
(1.1) |
|||||||||
π |
|||||||||||||
При этом пишут |
|
−π |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
∞ |
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
∑ |
|
|
|
|||||
f (x) ~ |
a0 |
+ |
|
|
(an cos nx + bn sin nx) |
(1.2) |
|||||||
|
|
|
|||||||||||
n=1
Поскольку построение ряда (1.2) выполнено формально, то этот ряд может расходиться или сходиться, но сумма его, вообще говоря, может не совпадать с разложенной в него функцией.
2.Сформулируем достаточные условия, при выполнении которых ряд (1.2) имеет сумму, равную заданной функции f (x):
Функция f (x) может иметь на отрезке [–π, π] лишь конечное число максимумов и минимумов и должна быть непрерывной, за исключением, быть может, конечного числа точек разрыва первого рода.
Эти условия называются условиями Дирихле.
Теорема Дирихле. Если функция f (x) удовлетворяет условиям Дирихле на отрезке [–π, π], то её ряд Фурье сходится к функции f (x) во
всех точках, в которых она непрерывна. В точках разрыва функции

23
ряд сходится к полусумме |
f (c − 0) + f (c + 0) |
её предельных значений |
|
2 |
|||
|
|
слева и справа (c – точка разрыва первого рода). Если f (−π) ≠ f (π) , то
в точках ± π ряд сходится к значению |
f (−π + 0) + f (π − 0) |
. При этом |
|
2 |
|||
|
|
сумма ряда (1.2) является периодической с периодом 2π функцией на всей оси Ox.
3. Пусть теперь функция f (x) задана на отрезке [–l, l]. Ряд Фурье в этом случае имеет вид
|
a0 |
|
|
|
∞ |
|
|
|
|
|
|
nπx |
|
|
nπx |
|
|
|||||
f (x) ~ |
+ |
|
∑ |
(an |
cos |
|
+ bn sin |
) , |
(3.1) |
|||||||||||||
2 |
|
|
|
|
l |
|
|
l |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 = |
|
∫ f (x) dx , |
|
|
|
||||||||||
|
|
|
|
|
|
|
l |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−l |
|
|
|
|
|
|
|
|
|
|
|
|
1 l |
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
||||||||
an = |
|
|
∫ f (x) cos |
|
|
|
dx |
(n =1, 2, ...) , |
|
|||||||||||||
l |
|
l |
|
|
||||||||||||||||||
|
|
|
|
|
−l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 l |
|
|
|
|
|
nπx |
|
|
|
|
|
|
||||||
bn = |
|
|
∫ f (x) sin |
|
|
|
dx |
(n =1, 2, ...) |
(3.2) |
|||||||||||||
l |
|
l |
|
|||||||||||||||||||
|
|
|
|
|
|
|
−l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вопрос о сходимости |
ряда |
(3.1), |
|
|
в |
свою |
очередь, |
определяется |
||||||||||||||
теоремой Дирихле, но на отрезке [–l, l], соответственно. Суммой ряда будет периодическая на всей числовой оси функция с периодом 2l.
Замечание: Значок ~ в (1.2) и (3.1) нужно понимать следующим образом: если f (x) удовлетворяет условиям Дирихле на [–π, π] и [–l, l] соответственно, то во всех точках её непрерывности значок ~ надо заменить знаком = и помнить, что в точках разрыва сумма ряда равна
полусумме левого и правого пределов f (x) в этих точках, |
а на концах |
||||||||
|
f (−π) + f (π) |
f (−l) + f |
(l) |
f (−π) ≠ |
f (π) |
( f (−l) ≠ f (l) |
|||
отрезка – |
|
|
|
|
|
, если |
|||
2 |
2 |
|
|||||||
|
|
|
|
|
|
|
|||
соответственно). |
|
|
|
|
|
|
|
|
|
Пример 1. Разложить функцию |
|
|
|
||||||
|
|
|
f (x) = 0, − 2 ≤ x ≤ 0, |
|
|
||||
|
|
|
|
x, |
0 < x ≤ 2 |
|
|
|
|
в ряд Фурье на интервале (–2, 2).
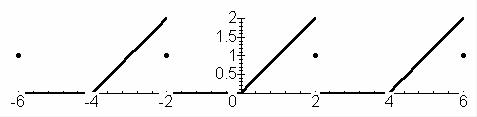
24
Рис. 1
|
a0 |
∞ |
nπx |
|
nπx |
|
|
f (x) = |
+ ∑(an cos |
+ bn sin |
) . Данная функция непрерывна |
||||
|
|
|
|||||
2 |
n=1 |
2 |
|
2 |
|
||
на отрезке [–2, 2] и не имеет там экстремумов, следовательно, удовлетворяет условиям Дирихле. Вычислим коэффициенты ряда:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 = |
|
∫0 dx + ∫x dx |
= |
|
|
|
|
|
|
|
|
|
=1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
u |
= x, du = dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
an = |
|
∫0 cos |
|
dx |
+ ∫x cos |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
2 |
|
|
|
|
nπx = |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
dv = cos |
|
|
|
|
, v = |
|
|
|
|
|
sin |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
nπ |
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
nπx |
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
= |
|
|
x |
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
dx |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 |
nπ |
|
2 |
|
|
0 |
|
nπ |
|
2 |
|
|
2 |
|
n |
2 |
|
π |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
n = 2k − чётное |
|
|
|
|
(k =1, 2, ...), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
(cos nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
−1) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
n = 2k −1 − нечётное; |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
2 π2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
π |
2 |
|
|
(2k −1) |
2 |
π |
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
u = x, |
du = dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
bn = |
|
|
∫0 sin |
|
|
dx + ∫x sin |
dx |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
nπx |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
dv |
= sin |
|
|
|
|
|
, v |
= − |
|
|
|
|
cos |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
nπ |
2 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
nπx |
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
= |
|
|
− |
x |
|
cos |
|
|
|
|
|
|
|
|
+ ∫ |
|
|
cos |
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
2 |
|
nπ |
2 |
|
|
|
|
|
0 |
nπ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
= |
|
|
|
|
nπ |
cos nπ + |
|
sin |
|
|
|
|
|
|
|
|
|
= |
|
(−1) |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
n2 π2 |
2 |
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Таким образом, разложение функции f (x) в ряд Фурье имеет вид |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2k −1)πx |
|
|
|
|
|
|
∞ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
f (x) = |
|
|
− ∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
+ ∑ |
|
(−1) n+1 sin |
. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(2k |
−1)2 π2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
n=1 nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
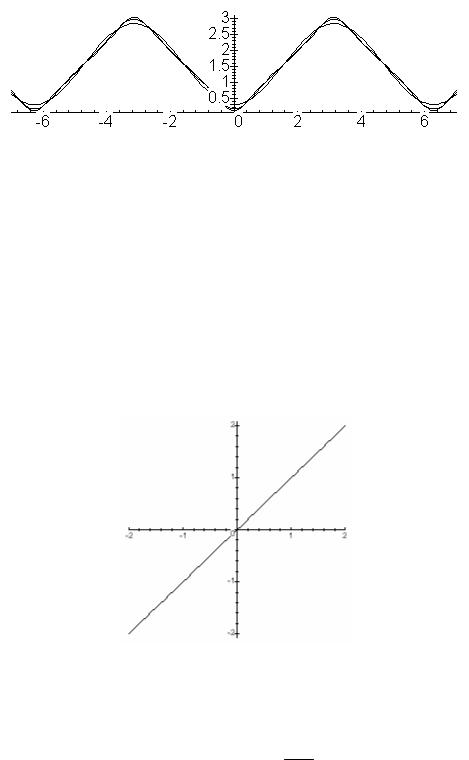
В соответствии с теоремой Дирихле, график суммы ряда Фурье для функции f (x) имеет вид
Рис. 2
4. Разложение в ряд Фурье чётных и нечётных функций.

25
а) Пусть функция f (x), заданная на отрезке [–l, l] – чётная и удовлетворяет условиям Дирихле. Тогда ряд Фурье для этой функции будет содержать только a0 и члены с косинусами, т. е.
|
|
|
a0 |
|
|
∞ |
|
nπx |
|
|
||
|
|
f (x) = |
|
+ ∑an cos |
, |
(4.1) |
||||||
|
|
|||||||||||
|
2 l |
2 |
|
|
n=1 |
|
l |
|
||||
|
nπx |
|
|
|
|
|
||||||
an = |
|
∫ f (x) cos |
|
|
dx |
(n = 0, 1, 2, ...), bn |
= 0 . |
|||||
l |
l |
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|||
Пример 2. Разложить |
в |
ряд |
Фурье на отрезке |
[–π, π] чётную |
||||||||
функцию f (x) = |x|.
Рис. 3
Данная функция непрерывна на заданном отрезке (l = π) и имеет на нём один экстремум, поэтому удовлетворяет условиям Дирихле.
Ряд (4.1) в данном случае принимает вид
f (x) = a0 + ∑∞ an cos nx .
2 n=1
Так как f (x) = |x| = x при 0 ≤ x ≤ π, то
|
2 |
π |
2 |
|
x 2 |
|
π |
|
|
|
|
||||||
a0 = |
|
∫x dx = |
|
|
|
|
|
= π, |
π |
π |
2 |
|
|
||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
an = π2
=2 x sin nx
π n
0, n = 2k
= − 4 = −n 2 π
π |
|
|
|
u |
= x, du = dx, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
= |
|
|
|
||
∫x cos nx dx = |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
dv = cos nx dx, v = |
|
|
sin nx |
|
|
|
|
||||||
|
|
|
|
|
n |
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
π |
1 |
π |
|
2 |
|
|
|
|
2 |
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
− |
|
∫sin nx dx |
= |
|
(cos nπ − |
1) = |
|
|
((−1) |
|
−1) |
= |
||||
0 |
n |
πn 2 |
πn2 |
|
|
||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− чётное |
(k =1, 2, ...), |
|
||
4 |
|
, |
n = 2k −1 |
− нечётное. Следовательно, |
(2k −1)2 |
|
|||
π |
|
|
||
|
π |
∞ |
1 |
|
|
|
f (x) = |
− 4 ∑ |
|
|
cos (2k −1) x . |
||
2 |
(2k −1) |
2 |
|
|||
|
k =1 |
|
π |
|||
В соответствии с теоремой Дирихле, график суммы ряда Фурье – периодическая функция с периодом 2π, которая совпадает с f (x) на отрезке
[–π, π] (рис. 4).
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
|
|
|
|
||
|
|
|
|
|
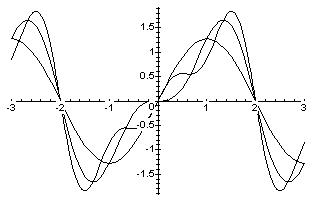
На рис. 5 изображены графики частичных сумм ряда Фурье S1 (x) = |
|||||||||||||||||
= |
π |
− |
|
4 |
cos x , |
S2 (x) = |
π |
− |
4 |
cos x − |
4 |
cos 3x , |
S3 (x) = |
π |
− |
4 |
cos x – |
|||||
2 |
|
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
π |
2 |
|
π |
9π |
|
|
π |
||||||||||
– |
4 |
|
cos 3x – |
4 |
cos 5x : |
|
|
|
|
|
|
|
|
|
|
|
||||||
9π |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
25π |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5
б) Пусть функция f (x), заданная на отрезке [–l, l] – нечётная и удовлетворяет условиям Дирихле. Тогда ряд Фурье для этой функции будет содержать только члены с синусами:
|
|
|
|
∞ |
nπx |
|
|
|
|
|
f (x) = ∑bn sin |
, |
|
|
|
|
|
l |
||
|
|
|
|
n=1 |
|
|
|
2 l |
|
|
|
||
|
nπx |
|
|
|
||
где bn = |
|
∫ f (x) sin |
|
dx (n = 0, 1, 2, ...) . |
|
|
l |
l |
|
|
|||
|
|
0 |
|
|
|
|
Пример 3. Разложить в ряд Фурье на отрезке [–2, 2] нечётную функцию f (x) = x.
Рис. 6 Эта функция на заданном отрезке удовлетворяет условиям Дирихле,
так как непрерывна и не имеет там экстремумов. Ряд Фурье для данной функции имеет вид
f (x) = ∑∞ bn sin nπx ,
n=1 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
nπx |
|
|
u = x, |
du = dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
∫x sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где bn |
= |
|
|
|
|
|
|
dx = |
|
|
|
|
nπx |
|
|
|
2 |
|
|
|
nπx |
= |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
dv |
= sin |
|
dx, v = − |
|
cos |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
nπ |
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
nπx |
|
|
|
2 |
|
|
2 |
2 |
|
nπx |
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
nπx |
|
|
2 |
|
||
= − x |
|
cos |
|
|
|
+ |
∫cos |
dx = − |
cos nπ + |
|
|
sin |
|
|
= |
||||||||||||||||||||
nπ |
|
|
|
|
nπ |
|
nπ |
|
2 |
2 |
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
0 |
|
|
0 |
2 |
|
|
|
|
|
|
|
n |
|
π |
|
|
2 |
|
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
(−1) |
n+1 |
4 |
|
. Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
nπ |
|
|
|
|
|
∞ |
(−1)n+1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
nπx |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
|
∑ |
sin |
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
n |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
На рис. 7 изображены графики частичных сумм ряда Фурье S1 |
||||||||||||||||||||||||||||
= |
|
4 |
sin |
πx |
, S2 (x) = |
4 |
sin |
πx |
− |
4 |
|
sin πx , S3 |
(x) = |
4 |
sin |
πx |
|
− |
4 |
sin πx |
||||||||||||
|
|
|
|
|
2 |
2π |
|
2 |
2π |
|||||||||||||||||||||||
|
|
π |
|
2 |
|
|
|
|
|
π |
|
|
|
|
|
π |
|
|
|
|||||||||||||
+ |
4 |
sin |
3πx |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7
(x) =
+
5.Разложение в ряд Фурье функций, заданных на отрезке [0, l].
Вэтом случае можно доопределить функцию на полуинтервал
[–l, 0) либо чётным, либо нечётным образом. В первом случае получится чётная на [–l, l] функция, которая будет раскладываться в ряд Фурье по косинусам, а во втором – нечётная на [–l, l] функция, и её ряд Фурье будет содержать только синусы. В обоих случаях на отрезке [0, l] эти ряды дадут разложение исходной функции в ряд Фурье.
Пример 4. Разложить функцию f (x) = x, заданную на отрезке [0, π], доопределив её чётным образом на полуинтервал [–π, 0).
Врезультате получим чётную функцию φ (x); для x < 0 будет φ (x) =
=φ (–x) = f (–x) = –x, следовательно, φ (x) = |x| на [–π, π]. Разложение этой функции было сделано в примере 2, и оно одновременно является разложением f (x) = x на отрезке [0, π].
Пример 5. Разложить функцию f (x) = x + 1, заданную на отрезке [0, 2], в ряд Фурье, продолжив её нечётным образом на полуинтервал [-2,0)

28
Рис. 8
В результате получим нечётную функцию φ (x); для x < 0 будет φ (x)
= – φ (–x) = – f (–x) = x – 1, следовательно, φ (x) = |
x −1, |
− 2 |
≤ x < 0, |
Эта |
|
0 ≤ x ≤ 2. |
|||
|
x +1, |
|
||
функция непрерывна на [–2, 2] за исключением точки x = 0, в которой она имеет разрыв первого рода, т. е. удовлетворяет условиям Дирихле:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ (x) = ∑bn sin |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
nπx |
|
|
|
|
u = x +1, du |
= dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где bn |
= |
|
|
(x +1) sin |
|
|
|
dx = |
|
|
nπx |
|
|
|
|
|
|
|
|
2 |
|
|
|
nπx |
= |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
dv = sin |
|
|
|
|
dx, v = − |
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
nπ |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|
nπx |
|
|
2 |
|
|
|
2 |
|
2 |
|
nπx |
|
|
|
|
2 |
|
|
[− 3 cos nπ +1] |
|
|
|
4 |
|
|
|
nπx |
|
|
2 |
|||||||||||||||
− (x +1) |
|
cos |
|
|
+ |
|
|
∫cos |
dx = |
|
|
+ |
|
|
|
sin |
|
|
|||||||||||||||||||||||||||||||||||
nπ |
|
|
|
|
|
nπ |
|
|
|
nπ |
|
|
2 |
2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
0 |
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
π |
|
|
2 |
|
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
[1 − 3 (−1)n ]= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
2 |
|
2 |
|
1 + 3 (−1)n+1 |
. Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
nπ |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
∞ |
(−1)n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
φ (x) = |
∑ |
1 + 3 |
sin |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В этот ряд одновременно разложена заданная на [0, 2] функция f (x) = x + 1. Замечание: Можно также разложить f (x) и на отрезке [0, l], но тогда в разложение войдут члены ряда и с синусами, и с косинусами, а сумма
ряда будет периодической функцией с периодом T = l.

29
Вариант № 1
1. Исследовать сходимость знакоположительных рядов.
|
∞ |
|
1 |
|
|
π |
|
∞ |
n!(2n +1)! |
||||||
1) |
∑ n |
sin |
n |
2) |
∑ |
|
|
|
|
||||||
(3n)! |
|||||||||||||||
|
|
|
|
||||||||||||
|
n=1 |
|
|
|
|
|
|
|
n=1 |
|
|
|
|
||
|
∞ |
1 |
n |
n |
|
∞ |
|
1 |
|
||||||
|
|
∑ |
|
|
|
||||||||||
3) |
∑ |
|
|
|
|
|
|
4) |
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|||||||
3 |
n |
|
|
|
(n +1) |
||||||||||
|
n=1 |
|
n +1 |
|
|
n=1 n ln |
|
||||||||
2.Исследовать сходимость знакопеременного ряда. Если он сходится, то указать абсолютно или условно.
∞ |
|
n n |
|
∑(−1)n |
|
|
|
|
|||
n=1 |
|
2n +1 |
|
|
|
|
|
3. Найти область сходимости степенного ряда.
∑∞ n +1 (x −2)n
n=1 n2 2n
4.Разложить функцию в ряд Тейлора по степеням х. Указать интервал, в котором это разложение имеет место.
9
20 − х − х2
5. Вычислить интеграл с точностью до 0,001.
1 − x 2
∫e 2 dx
0
6.Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего данному начальному условию y(0) = a .
y′=sin x + y2 ; y(0) =1
7.Данную функцию f (x) разложить в ряд Фурье в данном интервале. Построить график функции f (x) и график суммы ряда Фурье
f (x) =1 − x , (−2 < x < 2)

30
Вариант № 2
1. Исследовать сходимость знакоположительных рядов.
∞ |
|
|
|
|
∞ |
|
|
|
|
|
1) ∑ln n |
|
|
|
(2n)! |
|
|||||
|
2) |
∑ |
|
|
||||||
|
|
n |
||||||||
n=2 |
n |
|
|
n =1 |
2 |
+ 3 |
||||
∞ |
2n |
n |
|
∞ |
|
sin 2 n |
||||
3) ∑n4 |
|
|
4) |
∑ |
|
n |
2 |
+ 1 |
||
|
|
|||||||||
n =1 |
3n + 5 |
|
|
n =1 |
|
|||||
|
|
|
|
|
|
|
|
|||
2.Исследовать сходимость знакопеременного ряда. Если он сходится, то указать абсолютно или условно.
∞ |
(−1)n |
|
∑ |
||
(n +1)ln n |
||
n =1 |
||
|
3. Найти область сходимости степенного ряда.
∞ |
|
3n |
|
|
∑ |
|
|
(x −3)n |
|
n |
2 |
|||
n=1 |
+1 |
|
||
|
|
|
|
|
4.Разложить функцию в ряд Тейлора по степеням х. Указать интервал, в котором это разложение имеет место.
ch 3x −1
х2
5.Вычислить интеграл с точностью до 0,001.
2,5 |
dx |
|
∫ 4 |
4 |
|
0 |
625 + x |
|
6.Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего данному начальному условию y(0) = a .
y′= y + y2 ; y(0) =3
7.Данную функцию f (x) разложить в ряд Фурье в данном интервале. Построить график функции f (x) и график суммы ряда Фурье
f (x) =1 + x , (−1 < x <1)

31
Вариант № 3
1. Исследовать сходимость знакоположительных рядов.
∞ sin |
π |
|
|
|
|
∞ |
π |
|
||||
|
|
|
|
|||||||||
1) ∑ |
|
|
n |
|
|
2) |
∑n! sin |
|
||||
|
|
n |
|
|||||||||
|
7 |
|
|
n |
||||||||
n=1 |
|
|
|
|
n 2 |
|
n=1 |
2 |
|
|||
∞ |
|
|
n |
|
∞ |
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑n=1 (3n+1) ln2(n+2) |
||||||
|
|
|
|
|
|
|||||||
3) ∑n =1 10n + 5 |
|
4) |
||||||||||
2.Исследовать сходимость знакопеременного ряда. Если он сходится, то указать абсолютно или условно.
∞ |
|
(−1)n |
∑ |
|
|
2 |
n +1 |
|
n =1 |
(2n +1) |
3. Найти область сходимости степенного ряда.
∑∞ 5n (x + 2)n
n=2 n
4.Разложить функцию в ряд Тейлора по степеням х. Указать интервал,
вкотором это разложение имеет место.
x2
 4 − x
4 − x
5. Вычислить интеграл с точностью до 0,001.
1
∫1−cosx xdx
0
6.Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего данному начальному условию y(0) = a .
y′ = 2e y − xy ; y(0) = 0
7.Данную функцию f (x) разложить в ряд Фурье в данном интервале. Построить график функции f (x) и график суммы ряда Фурье
f (x) = |
π− x |
, (−π < x < π) |
|
2 |
|
