
- •Первые два вопроса:
- •Гармоническое колебание. Понятие комплексной амплитуды.
- •Комплексное сопротивление и комплексная проводимость цепи.
- •Описание процессов в электрических цепях. Методы анализа процессов в цепях.
- •Импульсная функция. Импульсная характеристика цепи.
- •Описание сигнала на выходе цепи с использованием импульсной характеристики. (Интеграл свертки).
- •Третьи вопросы:
-
Импульсная функция. Импульсная характеристика цепи.
Импульсная или δ-функция представляет импульс бесконечно малой длительности в точке t=0, имеющий бесконечно большую амплитуду и площадь, равную единице:

 ,
,
 .
.
Импульсную функцию можно рассматривать как предел, к которому стремиться прямоугольный импульс длительностью τ и амплитудой 1/τ при τ→∞
 Это
соотношение отражает фильтрующее
свойство импульсной функции.
Это
соотношение отражает фильтрующее
свойство импульсной функции.
Одной из важных характеристик линейной цепи является импульсная характеристика. Она представляет реакцию цепи (сигнал на выходе) на воздействие (сигнал на входе) в виде импульсной функции δ(t). Обозначается она h(t). Использование импульсной характеристики позволяет проводить анализ линейной цепи во времени.
|
|
-
Описание сигнала на выходе цепи с использованием импульсной характеристики. (Интеграл свертки).
Используя импульсную характеристику можно получить сигнал на выходе цепи при использовании сигнала на входе.
|
|
Сигнал произвольного вида
Сигнал может быть представлен в виде последовательности узких импульсов – импульсных функций
 ,
где Т – интервал разбиения по оси
времени.
,
где Т – интервал разбиения по оси
времени.
Тогда, с учетом принципа суперпозиции для линейной цепи выражение для сигнала на выходе цепи можем записать в виде
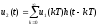 ,
где u1(t)
– сигнал на входе, h(t)
– реакция цепи на импульсное воздействие
– импульсная характеристика.
,
где u1(t)
– сигнал на входе, h(t)
– реакция цепи на импульсное воздействие
– импульсная характеристика.
Переходя
от дискретного сигнала к непрерывному,
вместо суммы запишем интеграл
 ,
где
,
где
 -
знак свертки (условное обозначение
интеграла свертки). Записанный интеграл
называется интегралом свертки или
интегралом Дюамеля. Он позволяет описать
сигнал на выходе цепи с известной
импульсной характеристикой при заданном
сигнале на входе.
-
знак свертки (условное обозначение
интеграла свертки). Записанный интеграл
называется интегралом свертки или
интегралом Дюамеля. Он позволяет описать
сигнал на выходе цепи с известной
импульсной характеристикой при заданном
сигнале на входе.
-
Соотношение между частотной характеристикой и импульсной характеристиками цепи.
Если гармонический сигнал на входе цепи представить в виде u1(t)=Re[Ů1eiωt], где Ů1=U1=const, то комплексный сигнал на выходе цепи, имеющей импульсную характеристику h(t), с учетом интеграла свертки определиться как
 ,
,
 .
Из записанного выражения следует
.
Из записанного выражения следует
 .
Таким образом, частотная характеристика
линейной цепи представляет преобразование
Фурье импульсной характеристики.
Обратное преобразование Фурье позволяет
перейти от частотной характеристики
цепи к импульсной
.
Таким образом, частотная характеристика
линейной цепи представляет преобразование
Фурье импульсной характеристики.
Обратное преобразование Фурье позволяет
перейти от частотной характеристики
цепи к импульсной
 .
.
Третьи вопросы:
-
Определить комплексное сопротивление цепи.
-
Определить частотную характеристику цепи (заданного вида).
-
Определить АЧХ цепи.
-
Определить сигнал на выходе цепи с использованием интеграла свертки.
-
Составить и решить уравнение для цепи первого порядка.
-
Записать выражение для импульсной характеристики цепи заданного вида.
-
Записать выражение для характеристики цепи с известной импульсной характеристикой.
