Потоком вектора через ориентированную поверхность называется поверхностный интеграл второго типа

. (14)

Выведем эту формулу, исходя из физического смысла введённого понятия. Рассмотрим частный случай стационарного поля, когда скорость течения жидкости во всех точках поля одна и та же (см. рис. 7). Количество жидкости Q, протекшее за единицу времени через прямоугольник со скоростью , равно произведению его площади на скорость :

.

Величина Q постоянна в любом сечении, параллельном данному.

Очевидно, что это же количество жидкости протечёт и через площадку ABCD, составляющую угол с прямоугольником A’B’C’D’. Тогда

,

где S - площадь ABCD,

, (15)

где - проекция скорости на нормаль .

Разумеется, формула будет верна для площадки любого вида, например, как на рис. 8.

Рис. 7                                                                  Рис. 8

Перейдём к общему случаю. Решим задачу о вычислении количества жидкости, протекшего через произвольную поверхность . Пусть в некоторой части пространства задано поле скоростей жидкости, т.е. в каждой точке M(x, y, z) этого пространства задан переменный вектор скорости

.

Рис. 9

Возьмём гладкую ориентированную поверхность (рис. 9) и подсчитаем количество жидкости, протекающее через эту поверхность. Разобьём поверхность сетью произвольных кривых на п участков , в каждом из которых выберем произвольную точку M_i. Будем считать, что каждая площадка , в силу её малости, плоская и поток, проходящий через неё, - постоянный, именно такой, как в точке M_i в направлении нормали ni, построенной в точке M_i.

Можно приближённо подсчитать количество жидкости, протекшее через поверхность по формуле (15), суммируя результаты по всем i = 1, 2, …, n :

, (16)

где - площадь участка,

- скорость поля в точке M_i,

- угол между нормалью к поверхности , построенной в точке M_i, и вектором скорости .

Преобразуем формулу (16), используя свойства скалярного произведения вектора на единичный вектор нормали

Перейдём к пределу при , когда, т. е. каждая площадка стягивается в точку:

.

Величина Q называется потоком жидкости через поверхность и выражается поверхностным интегралом (сравните с формулой 11 Темы 15)

 (17)

или . (18)

Таким образом, мы получили различные формулы для вычисления потока векторного поля с помощью поверхностных интегралов первого и второго типов.

Пример 6. Вычислить поток вектора через полную поверхность эллипсоида 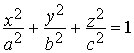в сторону внешней нормали.

Решение. Подынтегральная функция терпит разрыв в точке (0, 0, 0) - центре эллипсоида. Формулу Остроградского нельзя применять, хотя поверхность и замкнута, но можно воспользоваться формулой (17), связывающей поверхностные интегралы первого и второго типов:

2. Дифференциальная форма

Дифференциальная форма общего уравнения непрерывности такова:

где

• ∇• - дивергенция,

• t - время,

• σ добавление q на единицу объёма в единицу времени. Члены которые добавляют (σ > 0) или удаляют (σ < 0) q называются "источниками" и "стоками" соответственно.

Это общее уравнение может быть использовано для вывода любого уравнения непрерывности, начиная с простого уравнения неразрывности и до уравнения Навье-Стокса.

Если q сохраняющаяся величина, которая не может быть создана или уничтожена (например энергия), тогда σ = 0, и уравнение непрерывности принимает вид:

3. Возьмем несжимаемую жидкость и рассмотрим в ней трубку тока. Объём жидкости, прошедшей через поперечное сечение Sза время Dt, равенSvDt.

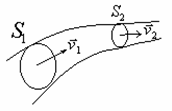
Тогда  Q = Sv  - поток жидкости, т.е. объём жидкости, прошедшей через поперечное сечениеSза единицу времени.

 

Если жидкость несжимаема, то объем жидкости между сечениями S₁ иS₂будет оставаться неизменным, и тогдаS₁v₁ = S₂v₂. Это справедливо для любой парыS₁ иS₂, и мы получаем

            Sv = const–теорема о неразрывности струи:

 Для несжимаемой жидкости величина потока жидкости Sv в любом сечении одной и той же трубки тока должна быть одинаковой.

4. Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Здесь

 — плотность жидкости,

 — скорость потока,

 — высота, на которой находится рассматриваемый элемент жидкости,

 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

 — ускорение свободного падения.

5. Трубка Пито–Прандтля.

Трубка Пито–Прандтля (см. рис. 3.6) позволяет одновременно определить величину динамического и статического давления в определенной точке потока.

Через отверстие А происходит измерение динамического давления. Через отверстия М измеряется статическое давление жидкости. Жидкость под действием давления поднимается по соответствующим пьезометрическим трубкам до точек А¢ и М¢.

Рис. 3.6. Трубка Пито–Прандтля

Так как плотность газа (воздуха) значительно меньше плотности жидкости, то давлением воздуха можно пренебречь. Разность давления в точках А и М будет . Разность давления Δp зависит от динамического давления на входе в трубку Пито–Прандтля, что следует из уравнения Бернулли для точек А и М:

,

где  – скорость потока на входе в трубку Пито–Прандтля. Таким образом,

,

откуда получаем

6. Фо́рмула Торриче́лли – связывает скорость истечения жидкости из малого отверстия в открытом сосуде с высотой жидкости над отверстием^[1].

Формула Торричелли утверждает, что скорость истечения жидкости через отверстие в тонкой стенке, находящееся в ёмкости на глубинеот поверхности, такая же, как и у тела, свободно падающего с высоты, то есть

где –ускорение свободного падения.

Последнее выражение получено в результате приравнивания приобретённой кинетической энергии и потерянной потенциальной энергии.

Эта формула была получена (хотя и не в приведённой выше форме) итальянским учёным Эванджелиста Торричелли, в 1643 году. Позже было показано, что эта формула является следствием закона Бернулли.

7. Закон Стокса, математическим выражением которого является формула Стокса, описывает взаимодействие между неподвижной безграничной вязкой жидкостью и помещенным в нее движущимся равномерно и прямолинейно телом. В соответствии с механическим принципом относительности, такая задача эквивалентна задаче об обтекании неподвижным телом набегающего на него стационарного потока жидкости, скорость v₀ которого вдали перед телом равна - u.

При обтекании тела потоком несжимаемой (div v = 0) жидкости (рис. 1), соответствующим малым значениям числа Рейнольдса

 

Re = v₀ l /n <<1,

 

где l - характерный линейный размер тела;

n - кинематическая вязкость жидкости,

 

уравнение движения вязкой жидкости (урравнение Навье-Стокса) может быть представлено в следующей приближенной форме:

 

v  grad p  0

 

или

 

rot v  0,

 

где  - динамическая вязкость жидкости;

p - давление;

 - оператор Лапласа.