
- •1. Содержание математического программирования. Постановка общей и основной задач линейного программирования.
- •1. Линейное программирование
- •1.1. Примеры задач линейного программирования
- •1.2. 0Бщая и основная задачи линейного программирования
- •2. Свойства задач линейного программирования. Графический метод решения задач линейного программирования.
- •1.3. Свойства задач линейного программирования
- •1.4.1. Графический метод решения задач линейного программирования
- •3. Алгоритм симплекс-метода решения общей задачи линейного программирования.
- •1.4.2. Симплекс-метод
- •Алгоритм симплекс-метода
- •4. Метод искусственного базиса
- •1.4.3. Методы искусственного базиса
- •5. Двойственная задача линейного программирования. Экономическая интерпретация двойственной задачи линейного программирования.
- •1.5. Двойственная задача линейного программирования
- •1.5.1. Экономическая интерпретация двойственной задачи
- •6. Постановка транспортной задачи. Методы нахождения первого допустимого решения транспортной задачи.
- •1.6. Транспортная задача
- •1.6.1. Пocтaнoвкa тpaнcпopтнoй зaдaчи
- •1.6.2. Методы нахождения начального допустимого плана перевозок груза
- •1. Правило "северо-западного yглa"
- •2. Метод наименьшей стоимости
- •7. Метод потенциалов.
- •1.6.3. Метод потенциалов
- •Алгоритм решения транспортной задачи методом потенциалов
4. Метод искусственного базиса
1.4.3. Методы искусственного базиса
Многие практические задачи линейного программирования не содержат линейно независимой системы единичных векторов Рj, которую можно выбрать в качестве первого базиса задачи. В этом случае в задачу вводят дополнительно k единичных векторов Рn+1,...,Pn+к, образующих базис.
Пусть задана следующая основная задача линейного программирования:
![]()
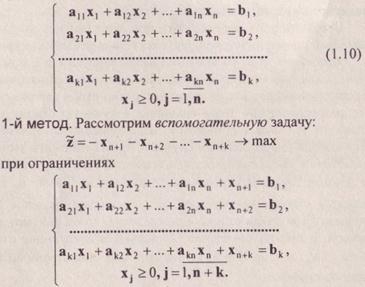
Переменные хn+1,…,xn+k называются искусственными, а связанная с ними система векторов Pn+1,…,Рn+k - искусственным базисом вспомогательной задачи. Следует здесь заметить, что если среди векторов Рj есть векторы, которые могут быть элементами базиса, то в соответствующие равенства исходной системы ограничений нет смысла вводить искусственные переменные.
Теперь к вспомогательной задаче можно применить симплекс-метод и найти ее решение.
Теорема
1.6.
Вспомогательная задача всегда разрешима.
При этом mах ![]() <=
0. Если mах
<=
0. Если mах![]() =
0 и достигается на плане
=
0 и достигается на плане=(
1,...,
n,
n+1,...,
n+k),
то вектор х=(
1,...,
n)
является опорным планом исходной задачи
(1.9), (l.10). Если mах
![]() <
0, то система условий (1.10) несовместна.
<
0, то система условий (1.10) несовместна.
Продолжая итерации симплекс-метода для модифицированной последней симплекс-таблицы вспомогательной задачи, найдем решение исходной задачи. Модификация симплекс-таблицы состоит в удалении искусственных переменных и замене коэффициентов целевой функции вспомогательной задачи на соответствующие коэффициенты целевой функции (1.9).
2-й метод. Рассмотрим следующую расширенную задачу, часто называемую М-задачей :

где М- некоторое достаточно большое положительное цисло, конкретное значение которого обычно не задается.
Переменные хn+1,..,xn+k также называют искусственными, а связанная с ними система векторов Pn+i ,…, Рn+к - искусственным базисом расширенной задачи.
Теорема 1.7. Если в оптимальном плане расширенной задачи (1.11), (1.12) все искусственные переменные равны нулю, то полученное оптимальное решение является решением исходной задачи (1.9), (1.10). Если в оптимальном плане расширенной задачи (1.11), (1.12) хотя бы одна искусственная переменная отлична от нуля, то исходная задача (1.9), (1.10) решения не имеет.
В
этом методе, искусственного базиса
исходные данные расширенной задачи
заносятся в таблицу, которая содержит
на одну строку больше, чем обычная
симплекс-таблица. Это связано с тем, что
разности :![]() j
(
j
(![]() j
=d+
еМ )
состоят из дух частей, одна из которых
зависит от M, а другая - нет. В(k+2)-ю строку
помещаются коэффициенты при М, а в
(k+1)-ю - слагаемые, не содержащие М.
j
=d+
еМ )
состоят из дух частей, одна из которых
зависит от M, а другая - нет. В(k+2)-ю строку
помещаются коэффициенты при М, а в
(k+1)-ю - слагаемые, не содержащие М.
При переходе от одного опорного плана к другому в базис вводят переменную, соответствующую наименьшему отрицательному числу (k+2)-й строки. Искусственная переменная, исключенная из базиса в результате некоторой итерации, в дальнейшем не вводится ни в один из последующих базисов, и преобразование столбца симплексной таблицы, соответствующего этой переменной, не производится.
Пересчет симплекс-таблиц при переходе от одного опорного плана к другому производится по общим правилам симплекс-метода. Итерационный процесс по (k+2)-й строке ведут до тех пор, пока:
1) либо все искусственны е переменные не будут исключены из базиса;
2) либо не все искусственны е переменные исключены из базиса, но (k+2)-я строка не содержит больше отрицательных элементов в столбцах векторов Р1,..., Рn+к :
В первом случае базис отвечает некоторому опорному плану исходной задачи, и определение ее оптимального плана продолжают по (k+1)-й строке симплекс-таблицы.
Во втором случае, если элемент, стоящий в (k+2)-й строке столбца вектора Ро, отрицателен, то исходная задача не имеет решения; если же он равен нулю, то найденный опорный план исходной задачи является вырожденным и базис содержит по крайней мере один из векторов искусственного базиса.
