Алгоритм симплекс-метода

 

Рассмотрим алгоритм симплекс метода применитетельно к общей задаче ЛП. На предварительном шаге алгоритма определяется возможность применения симплекс-метода к задаче ЛП.

Шаг 0. Прежде чем применять симплекс-метод к общей задаче линейного программирования, ее следует привести к каноническому виду. После приведения задачи к каконическому виду будем иметь:

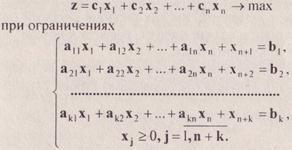
Векторы Р_n+1,…,_Pn+k образуют базис. Если из векторов Р1 системы ограничений нельзя указать базис, то к такой задаче ЛП симплекс-метод напрямую не применяется.

Дальнейший вычислительный пpoцeсс удобнее вести, если условия задачи записать н следующей симплекс-таблице:

 

Базис

СБ

C1

C2

…

Cn+1

…

Cn+k

bi

i

X1

X2

…

Xn+1

…

Xn+k

Xn+1

Cn+1

a11

a12

…

1

…

0

b1

1-е уравнение

…

…

…

…

…

…

…

…

…

…

Xn+k

Cn+k

ak1

ak2

…

0

…

1

bk

k-е уравнение

j>=0

1

2

…

n+1

…

n+k

z

Строка индексов

 

Шаг 1. По симплекс-таблице определяется опорное решение следующим образом: все свободные переменные приравниваются нулю, а базисные - соответствующим значениям столбца bi; . Начальный опорный план имеет вид: Х⁽⁰⁾ =(0,...,0,b₁,...,b_k). Проверим его на оптимальность, для этого заполним строку индексов в таблице. произведя следующие вычисления:

 

 - значение целевой функции в гочке Х^(о).

 

Если в строке индексов нет отрицательных оценок, то вычисления следует завершить, так как текущий опорный план оптимален. В противном случае следует перейти к новому опорному решению, т. е. изменить базис.

Шаг 2. Для смены базиса Выбираются ведущий (разрешающий) столбец и ведущая (разрешающая) строкаиз следующих условий:

Ведущая строка показывает, какая переменная будет из нового базиса удалена, а ведущий столбец - какая переменная будет в новый базис включена.

Если в ведущем столбце нет а_i > 0, то исходная задача не имеет конечного рецаения (т. е. mах z=+).

Шаг 3. Строится новая симплекс-таблица, в которой вместо базисной переменной х, включена х. Новые коэффициенты аij и bi пересчитываются по следующим формулам:

Перейти к шагу 1.

Последовательное выполнение вычислений шагов 1-3 составляет одну итерацию симплекс-метода.

Итерации повторяется до тех пор, пока не будет найден оптимальный план или установлено отсутствие решения задачи.

Замечание. При выполнении вычислений шага 2 может получиться так, что минимум отношения окажется одинаковы м для нескольких номеров i, т. е. сразу несколько строк таблицы могут быть разрешающими. Если выбирать ведущую строку произвольно, то это может привести к зацикливанию алгоритма симплекс-метода (вырожденный случай). Чтобы избежать этого, рекомендуется этот выбор осуществлять по следующему правилу: для данных строк таблицы вычисляются отношения: а_i1/а_i и находится строка, для которой это отношение является минимальным. Если такая строка единственная, то ее считают разрешающей. В противном случае вычисляются следующие отношения: а_i1/а_i и т. д. В результате получим единственную разрешающую строку.