
- •1. Содержание математического программирования. Постановка общей и основной задач линейного программирования.
- •1. Линейное программирование
- •1.1. Примеры задач линейного программирования
- •1.2. 0Бщая и основная задачи линейного программирования
- •2. Свойства задач линейного программирования. Графический метод решения задач линейного программирования.
- •1.3. Свойства задач линейного программирования
- •1.4.1. Графический метод решения задач линейного программирования
- •3. Алгоритм симплекс-метода решения общей задачи линейного программирования.
- •1.4.2. Симплекс-метод
- •Алгоритм симплекс-метода
- •4. Метод искусственного базиса
- •1.4.3. Методы искусственного базиса
- •5. Двойственная задача линейного программирования. Экономическая интерпретация двойственной задачи линейного программирования.
- •1.5. Двойственная задача линейного программирования
- •1.5.1. Экономическая интерпретация двойственной задачи
- •6. Постановка транспортной задачи. Методы нахождения первого допустимого решения транспортной задачи.
- •1.6. Транспортная задача
- •1.6.1. Пocтaнoвкa тpaнcпopтнoй зaдaчи
- •1.6.2. Методы нахождения начального допустимого плана перевозок груза
- •1. Правило "северо-западного yглa"
- •2. Метод наименьшей стоимости
- •7. Метод потенциалов.
- •1.6.3. Метод потенциалов
- •Алгоритм решения транспортной задачи методом потенциалов
1.4.1. Графический метод решения задач линейного программирования
Графическим методом в основном решаются задачи с малым числом переменных. Он включает следующие этапы:
1. Строится многогранник решений.
Геометрический смысл системы ограничений состоит в следующем: уравнение а11х1+…+а1nхn=b1 представляет собой гиперплоскость в n-мерном пространстве, неравенство же есть точки подпространства, лежащие по одну сторону от гиперплоскости и образующие выпуклое множество. Следовательно, система ограничений (1.2) задачи линейного программирования есть множество точек n-мерного пространства, причем это множество выпуклое и каждая точка является решением системы неравенств.
2.
Находятся вектор ![]() =
grad z=(
=
grad z=(![]() 1,...,
1,...,![]() n)и
вершина многоугольника решений, на
которой достигается mах
z.
n)и
вершина многоугольника решений, на
которой достигается mах
z.
Известно,
что вектор-градиент функции z показывает
направление наибольшего роста функции.
Строится линия уровня с1х1+...+сnхn =h,
проходящая через начало координат.
Линия уровня обладает замечательным
свойством: после подстановки координат
лю6ой ее точки в выражение целевой
функции z последняя
принимает постоянное значение. Далее
перемещаем линию уровня в направлении
вектора ![]() до
тех пор, пока не будет достигнута угловая
вершина многоугольника решений либо
установлена неограниченность функции
на множестве решений.
до
тех пор, пока не будет достигнута угловая
вершина многоугольника решений либо
установлена неограниченность функции
на множестве решений.
3. Определяются координаты угловой вершины, являющиеся оптимальным планом, и значение целевой функции в этой точке.
Замечание. При нахождении решения задачи линейного программирования графическим методом могут встретиться случаи, изображенные на следующих рисунках.

На первом рисунке изображен случай, когда целевая функция принимает максимальное значение в единственной точке М. Из второго рисунка видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ. На третьем рисунке изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений.
Отметим, что нахождение минимального значения целевой функции отличается от нахождения её максимального значения лишь тем, что линия уровня c1x1+...+сnхn=hперемещается не в направлении вектора с, а в противоположном направлении.
3. Алгоритм симплекс-метода решения общей задачи линейного программирования.
Метод искусственного базиса.
1.4.2. Симплекс-метод
Учитывая теоремы 1.2, 1.3 и 1.4, для решения задачи линейного программирования можно предложить такую схему вычислений:
- среди векторов Р1,...,Рn выбрать k линейно независимых;
- найти опорный план, связанный с этой системой векторов;
- вычислить значение целевой функции для опорного плана.
Перебирая,
таким образом, все опорные планы данной
задачи и сравнивая между собой полученные
значения целевой функции, найдем
оптимальный план. Количество всех
переборов определяется по следующей
формуле: ![]() .
.
При достаточно большом количестве переменных исходной задачи такой перебор крайне затруднителен. В 40-х гг. ХХ в. американский математик Данциг предложил алгоритм разумного перебора опорных планов, получивший название симплекс-метода. Он позволяет найти вершину многогранника решений и определить, является ли она точкой экстремума целевой функции. Если нет, то обеспечивается переход в соседнюю вершину, где значение целевой функции больше предыдущего. Через конечное число подобных шагов точка экстремума функции z либо оказывается найденной, либо признается несуществующей. Симплекс-метод используется тогда, когда уже получено некоторое допустимое решение для ограничений (1.2), что равносильно приведению общей задачи линейного программирования к каноническому виду.
Рассмотрим
общую схему симмекс-метода применительно
к невырожденному случаю. Пусть
известен некоторый опорный план .
Для простоты изложения, не нарушая
общности, будем полагать:
=(
1,
2,...,
k,0,...,0)
с системой нeзависимых векторов

Определение 1.9. Если из некоторой системы векторов можно составить единичную матрицу, то такую систему векторов называют базисом.
Система единичных векторов Рj является базисом. Соответствующие базису переменные будем называть базисными переменными, а остальные - свободными перемеными.
Из (1.3) имеем:
1P1 +
2Р2...+
kРk =Р0. (1.4)
Обозначим
через ![]() значение
целевой функции, вычисленное для опорного
плана
значение
целевой функции, вычисленное для опорного
плана:
![]() =c1
=c11
+с2
2
+...+ck
k. (1.5)
Разложение
векторов Рj (j= ![]() )
по базису имеет вид:
)
по базису имеет вид:
Рj =а1j Р1 +а2j Р2 ...+akjPk . (1.6)
Для
фиксированногo j Е ![]() выберем
некоторое число
выберем
некоторое число![]() i
> 0 и вычтем
i
> 0 и вычтем![]() i
x (l.6) из (1.4), тогда получим :
i
x (l.6) из (1.4), тогда получим :
Р0 =(1-
![]() iaij)P1 +...+(
iaij)P1 +...+(k -
![]() iakj)Рk+
iakj)Рk+![]() iРj.
iРj.
Введем обозначение
![]() =(
=(1-
![]() ia1j,...,
ia1j,...,k-
![]() iakj,0,...,
iakj,0,...,![]() i,0,...0).
i,0,...0).
Если ![]() i выбрать
из условия
i выбрать
из условия
![]() i
=min{
i
=min{/аij:аij
> 0,i=
![]() }, (1.7)
}, (1.7)
то ![]() —
план исходной задачи. Обозначим
через
—
план исходной задачи. Обозначим
через![]() значение
целевой функции, вычисленное для этого
плана, которое имеет вид:
значение
целевой функции, вычисленное для этого
плана, которое имеет вид:
![]() =c1(
=c1(1-
![]() iа1j)+...+ck(
iа1j)+...+ck(k -
![]() iakj)+сj
iakj)+сj![]() i (1.8)
i (1.8)
Обозначим через z(j) следующее выражение:
z(J)=c1a1j +...+ckakj.
Вычтем ![]() i х z(j)
из (1.5), получим :
i х z(j)
из (1.5), получим :
![]()
Отсюдa
и (1.8) имеем: ![]() =
=![]() -
-![]() i(z(j)-cj)=
i(z(j)-cj)= ![]() -
-![]() i
i![]() jгде
jгде ![]() j=z(j)-cj
j=z(j)-cj
Таким образом, пришли к следующему условию оптимальности.
Теорема
1.5. Опорный
план =(
1,
2,...,
k,0,...,0)
задачи линейного программирования
являетсяоптимальным, если
выполняется неравенство
![]() j>=
0 для любого номера j=
j>=
0 для любого номера j= ![]() .
.
Пусть
для некоторого номера j= ![]() выполняется
соотношение
выполняется
соотношение
![]()
Если
среди чисел аi![]() (i
=
(i
=![]() )
нет положительных, то план
)
нет положительных, то план![]() не
является опорным, так как содержит k+1
отличную от нуля компонeнтy. В зтом случае
целевая функция ислодной задачи не
oгpaничена на множестве ее планов.
не
является опорным, так как содержит k+1
отличную от нуля компонeнтy. В зтом случае
целевая функция ислодной задачи не
oгpaничена на множестве ее планов.
Если
же для некоторых индексов i Е ![]() :
аi
:
аi![]() >
0, то покажем, что план
>
0, то покажем, что план ![]() -
опорный план. Для этого достаточно
показать, чтo система векторов
Рj(J=1,...,
-
опорный план. Для этого достаточно
показать, чтo система векторов
Рj(J=1,...,![]() -1,
-1,![]() +1,...,k),Р
+1,...,k),Р![]() линейно
независима (
линейно
независима (![]() -
индекс i, на котором достигается минимум
в(1.7)).
-
индекс i, на котором достигается минимум
в(1.7)).
Покажем
это от противного. Пусть указанная
система векторов линейно не зависима.
Тогда можно указать числа ![]() ,
,![]() 1,...,
1,...,![]() k,
среди которых имеются ненулевые такие,
что
k,
среди которых имеются ненулевые такие,
что
![]()
Подставляя
в эту формулу разложение вектора Р![]() из
(1.6}, получим следующее:
из
(1.6}, получим следующее:
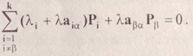
Система
векторов Р1,...,P![]() ,...,Pk линейно
независима, а а
,...,Pk линейно
независима, а а![]() >
0. Это значит, что последнее coотношение
выполняется лишь при
>
0. Это значит, что последнее coотношение
выполняется лишь при ![]() .
Получили противоречие.
.
Получили противоречие.
