2.8. Изотермический процесс

Изотермическим называется процесс, протекающий при постоянной температуре.

Рис. 2.7. График изотермического процесса	Рис. 2.8. К определению внутренней энергии газа

1. Уравнение процесса – .

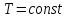2. График процесса. Из уравнения состояния следует, что , так как. Следовательно, графиком процесса вр,υ - координатах является равнобокая гипербола (рис. 2.7).

3. Связь между параметрами состояния газа. Для этого запишем уравнение состояния для точек 2 и 1 и разделим их друг на друга

, .

Так как в изотермическом процессе , то

. (2.20)

4. Теплоемкость газа в изотермическом процессе 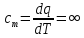, так как в этом процессе, а.

5. Определение количества теплоты q, подведенной к газу, совершенной им работы l и изменения его внутренней энергии Δu:

• изменение внутренней энергии , т.к.;

• согласно первому закону термодинамики . Так как = 0, то , где. Из уравнения состояния следует, что. Тогда. Таким образом, в изотермическом процессе

. (2.21)

Если , то, согласно равенству (2.21),. Значит, при подводе теплоты к газу его удельный объем возрастает и наоборот (рис. 2.7).

Таким образом, в изотермическом процессе теплота, сообщаемая газу, идет на совершение им работы расширения против внешних сил.

Используя график изотермического процесса (рис. 2.8), можно показать, что изменение внутренней энергии газа в любом процессе . Действительно, во всех процессахa, b и c, начинающихся в точке 0 и заканчивающихся на изотерме, изменение внутренней энергии будет одинаково, т.е. , так как начальное и конечное значение температуры в этих процессах одно и то же.

Но согласно первому закону термодинамики в изохорном процессе a теплота, подведенная к газу, идет только на увеличение его внутренней энергии, т.к. в этом процессе газ не совершает работу, т.е. . Как установлено выше, в изохорном процессе. Отсюда следует, что в любом процессе

.

Рис. 2.9. Графики адиабатного и изотермического процессов

2.9. Адиабатный процесс

Адиабатным называется процесс, протекающий при отсутствии теплообмена с окружающей средой (т.е. при q = 0).

1. Уравнение процесса.

Для вывода уравнения процесса запишем уравнение первого закона термодинамики в двух формах:

и

или в виде и.

Разделив второе уравнение на первое, получим

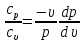или,

где – показатель адиабаты.

Проинтегрировав последнее уравнение, получим

или .

Откуда следует выражение для уравнения адиабатного процесса в виде

. (2.22) 2. График процесса. Из уравнения процесса (2.22) следует, что . Вр,υ - координатах – это неравнобокая гипебла.

Так как k >1, то адиабата протекает круче изотермы (рис. 2.9).

3. Связь между параметрами состояния газа. Для этого запишем уравнение адиабаты для точек 2 и 1 и разделим их друг на друга

, .

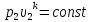Тогда получим

. (2.23)

Из уравнения состояния, записанного для точек 1 и 2 (рис. 2.9), следует, что . Используя соотношение (2.23), получим

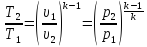. (2.24)

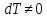4. Теплоемкость газа в адиабатном процессе. Так как в этом процессе , а, то

.

5. Определение количества теплоты q, подведенной к газу, совершенной им работы l и изменения его внутренней энергии Δu:

• количество тепла, подведенного к газу ;

• изменение внутренней энергии газа

;

• для адиабатного процесса по определению q = 0. Тогда из первого закона термодинамики следует, что при q = 0 работа расширения газа

, (2.25)

т. е. в адиабатном процессе работа газа совершается за счет убыли его внутренней энергии.Поэтому, как видно из формулы (2.25), адиабатное расширение газа (т.е. присопровождается уменьшением его температуры, а сжатиеповышением.

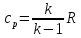Из уравнения Майера и выражения для показателя адиабатыследует, что,a , тогда

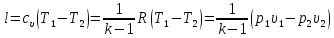. (2.26)