Способы измерения полного и статического давления газового потока

Статическое давление газового потока обычно измеряется путем подключения прибора для измерения давления (например, манометра) к отверстию в стенке канала (рис. 4.8а) или к отверстию на какой-либо поверхности, расположенной параллельно линиям тока. При этом важно, чтобы ось отверстия была перпендикулярна обтекаемой поверхности. Для измерения полного давления в поток вводится трубка полного напора (рис. 4.8б).

4.6. Уравнение сохранения энергии в параметрах заторможенного потока

Заменим в уравнении сохранения энергии, записанном в виде

,

сумму энтальпии и кинетической энергиис²/2 на выражение для энтальпии в параметрах заторможенного потока . Тогда получим уравнение сохранения энергии в параметрах заторможенного потока в виде

.

Таким образом, внешняя энергия в виде теплоты 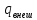и работы , подведенная к газу, расходуется на изменение его энтальпии в параметрах заторможенного потока (полной энтальпии).

Для идеального газа . Тогда уравнение энергии в параметрах заторможенного потока можно записать так:

.

Частные случаи уравнения сохранения энергии

а) Энергоизолированный поток (входные и выходные устройства, рис. 4.9 и рис. 4.10, каналы и т.д.).

В энергоизолированном потоке к газу не подводится и не отводится энергия в виде теплоты (и работы (=0). Поэтомууравнение сохранения энергии для любого газа в параметрах заторможенного потока приобретает вид: .

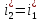Таким образом, в энергоизолированном потоке полная энтальпия газа остается постоянной.

Рис. 4.9. Схема дозвукового входного устройства				Рис. 4.10. Схема дозвукового выходного устройства

Для идеального газа, учитывая, что 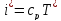, получим

.

Таким образом, в энергоизолированном потоке идеального газа его полная температура остается постоянной.

б) Теплоизолированный поток. В теплоизолированном потоке q_внеш=0. Но возможен обмен механической энергией с внешней средой, т.е. l_внеш  0. Тогда уравнение сохранения энергии для любого газа в параметрах заторможенного потока приобретает вид: ,

а для идеального газа: .

 Компрессор (рис. 4.4). В компрессоре q_внеш=0, но к воздуху через его вал подводится работа l_внеш =l_К , тогда

.

Следовательно, полная температура воздуха в компрессоре всегда повышается, причем это повышение пропорционально подведенной работе:

.

 Турбина (рис. 4.5). В турбине механическая работа отводится от газа через вал. Если эту работу обозначить l_Т , то l_внеш =  l_Т . Тогда

l _Т = i₁^*  i₂^* или .

Поэтому полная температура газа в турбине всегда снижается.

Заметим, что мощность на валу турбины, т.е. работа, производимая турбиной в единицу времени, равна произведению работы, отдаваемой вовне (через вал) единицей массы газа, на секундный расход газа, т.е.

N _Т = l_Т G _г .

Точно так же мощность, потребляемая компрессором, равна произведению работы, подводимой к единице массы воздуха, на его расход

N _К = l _К G _в .

 Камера сгорания. В камерах сгорания газотурбинных двигателей, теплообменных аппаратах и т.п. поток газа находится в условиях интенсивного подвода или отвода теплоты при отсутствии подводимой или отводимой механической работы. В таких случаях

или (для потока идеального газа)

.

Таким образом, теплота, подводимая к воздуху в камере сгорания, идет на увеличение его полной энтальпии (для идеального газа – на увеличение полной температуры).