Вычисление дисперсии ошибки исследуемой системы

Структура исследуемой системы приведена на рис. 4.2.

Рис. 4.2. Структурная схема лабораторной САУ.

Передаточная функция ошибки от полезного сигнала:

где К_пе = К_пС_п; К_ое = К₀С₀; p = s – оператор Лапласа;

Т₀₂= Т_и - искомый параметр.

Передаточная функция ошибки от помехи:

Полезный сигнал представляет собой синусоиду со случайной фазой

G(t) = Asin(₀t + f) ,

у которой фаза распределена по равномерному закону

P(f) = {1/(2) при | f |  ; 0 при | f | > }

Составляющая ошибки от полезного сигнала может быть вычислена по формуле (11). Спектральная плотность синусоидального сигнала представляет собой сумму двух -функций, расположенных на частотах ₀ и -₀:

S_g() = A²[( + ₀) + ( - ₀)]. (13)

После подстановки (13) в выражение (11) получается:

С учетом свойства -функции

можно записать

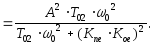
Составляющая D_en дисперсии D_e от помехи N(t) определяется следующим образом.

Рис. 4.3. Спектральная плотность помехи.

На рис. 4.3. приведен график спектральной плотности помехи. Из графика видно, что математическое ожидание помехи равно нулю. Величина S_no определяется из выражения

Отсюда

Верхняя _n2 и нижняя _n1 частоты спектра помехи и среднеквадратичное отклонение _n заданы.

Дисперсия ошибки от помехи согласно (12) определяется следующим образом:

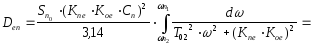
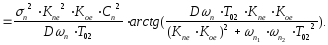
Суммарная дисперсия ошибки

(14)

Выражение (14) позволяет построить график зависимости дисперсии ошибки от постоянной времени Т₀₂. Характер этой зависимости показан на рис.4.4. Как видно из графика, функция D_e(T₀₂) имеет минимум при T_02опт.

Рис. 4.4. Графики зависимостей дисперсии ошибки САУ

от постоянной времени объекта управления.

Определение оптимального значения постоянной времени T_02опт является конечной целью данной лабораторной работы.

Значения параметров, входящих в формулу (14):

₀ = 6 c^-1; _n1 = 7,85 c^-1; _n2 = 126 c^-1; К_пС_п = 0,1; (C_п = 0,1); К₀С₀ = 10; (Co = 1); С_n_n = 13; (С_n = 1); D_n = _n2 - _n1 = 118,15;

T₀₂ = 0,011c - изменяется в ходе эксперимента.

Экспериментальное определение дисперсии.

В данной лабораторной работе сигнал ошибки e(t) проходит через квадратор, на выходе которого получается сигнал e²(t). Затем этот сигнал поступает на вход апериодического звена с постоянной времени Т.

Сигнал на выходе апериодического звена можно описать функцией:

где exp(-t/T)/T = L^-1{ 1/(Tp+1) } - весовая функция апериодического звена.

При T предел функции f(e) определяется следующей зависимостью:

Положив верхний предел равным Т и переобозначив переменную интегрирования, можно получить

Таким образом, если постоянная времени апериодического звена T, то на его выходе получается значение дисперсии ошибки D_e. Но, так как время наблюдения и постоянная времени не могут быть бесконечными, то фактически на выходе апериодического звена получается приближенная оценка дисперсии

Если время наблюдения выбрать равным постоянной времени Т, которая определяется из условия

T  50/_н,

где _н - низшая частота спектра случайного сигнала e²(t), то точность вычисления дисперсии составит примерно 2%, что вполне достаточно для практики. За низшую частоту спектра принимают частоту полезного сигнала ₀ = 6 c^-1. Тогда необходимая постоянная времени апериодического звена Т = 10 с, что и реализовано в лабораторном стенде.