контрольная по математике готовая

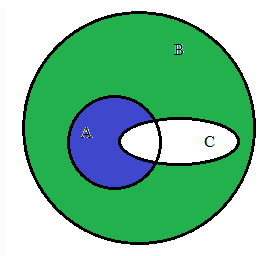
Задание 1. Доказать. Проиллюстрировать с помощью диаграммы Эйлера-Венна.

, то

Решение:

Если , то

Пусть . Доказать, что если , то . Действительно, . Учитывая условие , заключаем, что

Задание 2. Найти предел последовательности.

Решение:

Задание 3. Найти предел функции:

Решение:

Задание 4. Найти производные функции:

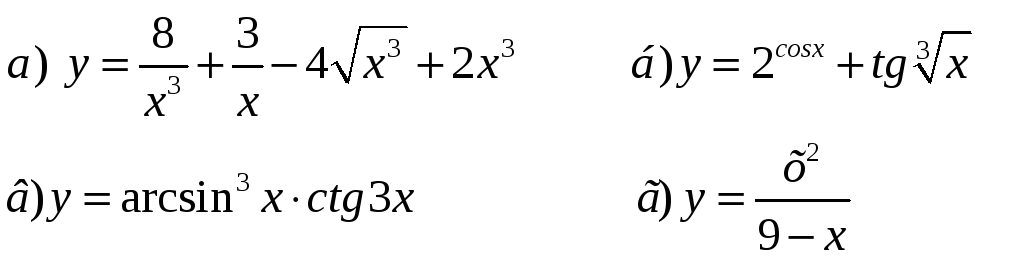
Решение:

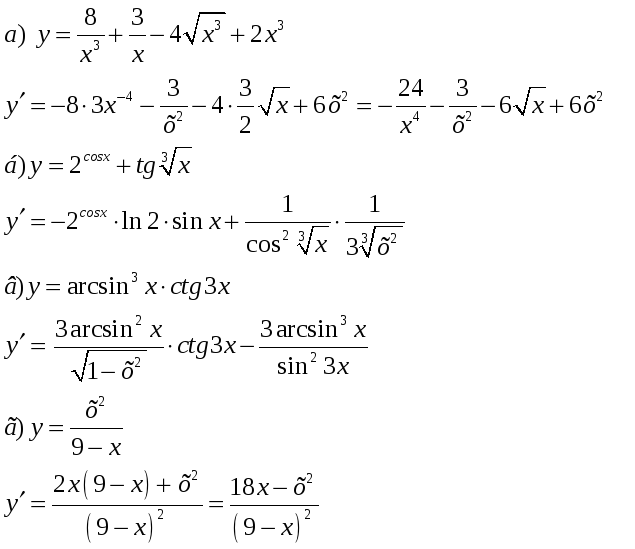
Задание 5. Найти данный предел, используя правило Лопиталя.

Решение.

Правило Лопиталя позволяет раскрывать неопределенность 0/0 и ∞ / ∞.

Для нашего примера:

Применим правило Лопиталя, которое гласит, что предел отношения функций равен пределу отношения их производных.

Для нашего примера:

f(x) = x-1

g(x) = ln(x)

Находим производные

f'(x) = 1

g'(x) = 1/x

Задание 6. Найти наибольшее и наименьшее значение функции.

y = x-1/x^2+3 [-2;3]

Необходимое условие экстремума функции одной переменной.

Уравнение f'₀(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает.

Достаточное условие экстремума функции одной переменной.

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:

f'₀(x*) = 0

f''₀(x*) > 0

то точка x* является точкой локального (глобального) минимума функции.

Если в точке x* выполняется условие:

f'₀(x*) = 0

f''₀(x*) < 0

то точка x* - локальный (глобальный) максимум.

Решение.

Находим первую производную функции:

y' = 1+2/x³

или

y' = (x³+2)/x³

Приравниваем ее к нулю:

1+2/x³ = 0

x₁ = -2^1/3

Вычисляем значения функции на концах отрезка

f(-2^1/3) = -3^1/3+3

f(-2) = 0.75

f(3) = 5.8889

Ответ: f_min = 0.75, f_max = 5.89

Задание 7. Исследовать функцию с помощью производной и построить график.

Решение:

Область определения функции:

Пересечение с осью абсцисс (OX):

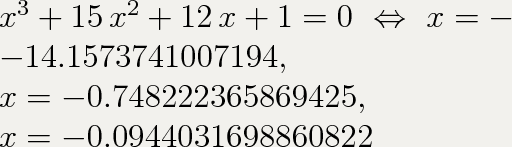
Пересечение с осью ординат (OY):

Поведение функции на бесконечности:

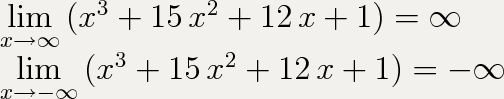
Исследование функции на чётность/нечётность:

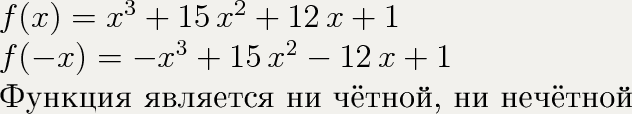
Производная функции равна:

Нули производной:

Функция возрастает на:

9Функция убывает на:

Минимальное значение функции:

Максимальное значение функции:

Ответ:

Построение графика функции

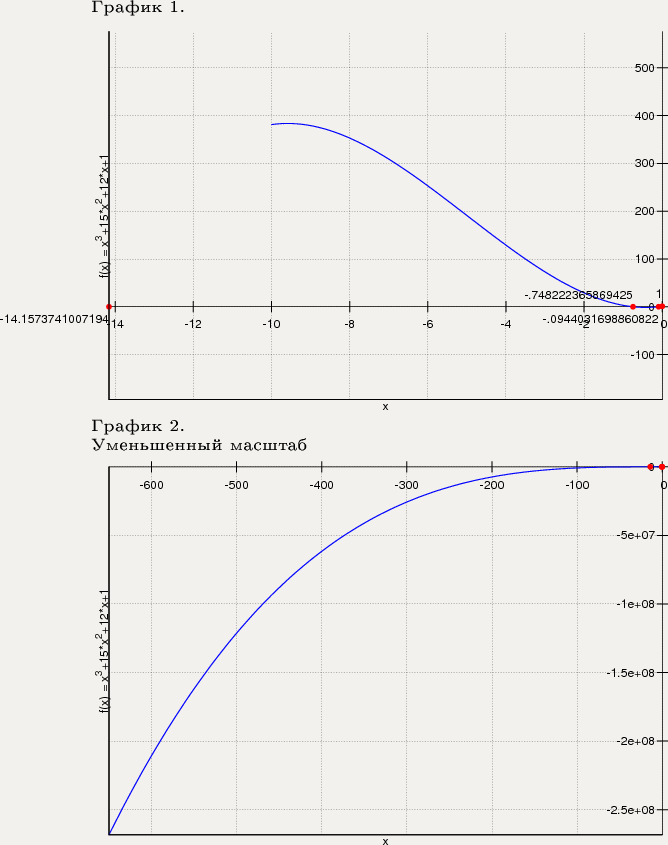
Задание 8. Найти неопределённые интегралы. Результат проверить дифференцированием.

а)

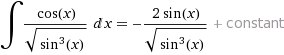
Решение:

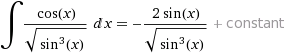
Альтернативные формы интеграла:

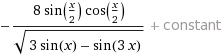
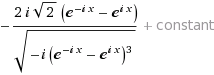
Альтернативная форма интеграла x>0:

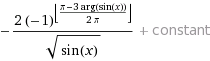
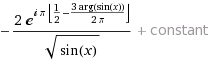
Разложение интеграла в точке x=0:

Разложение интеграла в точке х = 1 / (2 π):

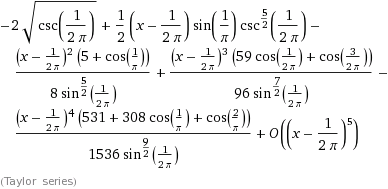
Разложение интеграла в точке х = 1 / π:

Разложение интеграла в точке х = π:

b) ∫ x arccosx dx

Решение:

Применим способ интегрирования по частям , где и

Вынесли константу из-под знака интеграла. Делаем замену переменных: Перепишем выражение:

Интеграл суммы есть сумма интегралов.

Проинтегрировали константу.

Вынесли константу из-под знака интеграла. Делаем замену переменных: Вынесли константу из-под знака интеграла.

Проинтегрировали косинус.

Сделали обратную замену.

Сделали обратную замену. Ответ:

Задание 9. Вычислить определённые интегралы.

Решение:

Задание 10. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертёж.

Решение:

Выполним построение фигуры, ограниченной параболой

и прямой :

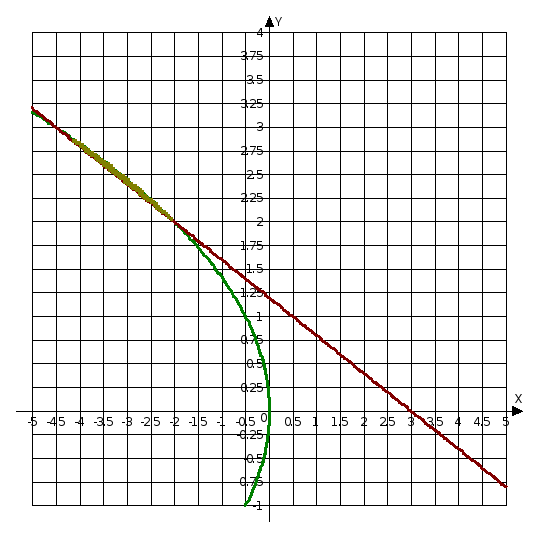
Найдём точки пересечения:

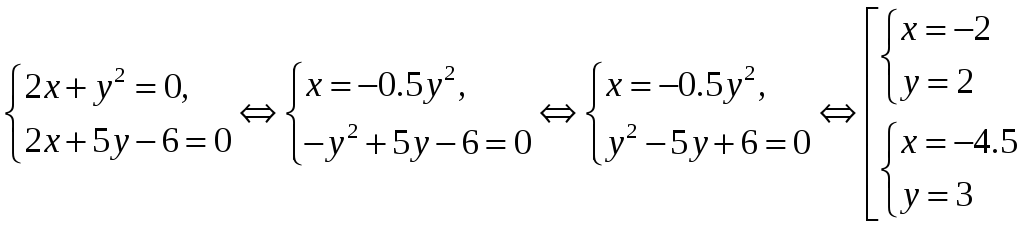
Находим площадь полученной области:

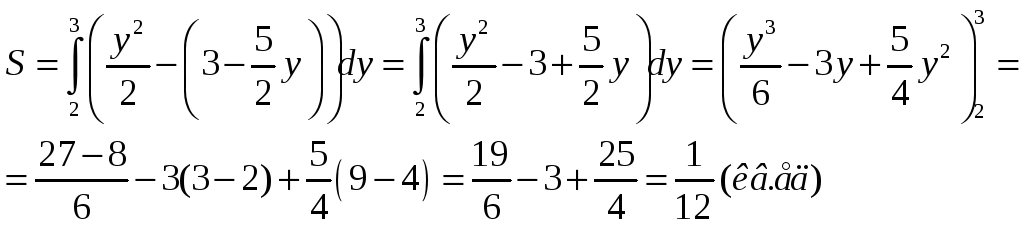
Задание 11. Найти общее решение уравнения первого порядка сетодом разделения переменных.

Решение:

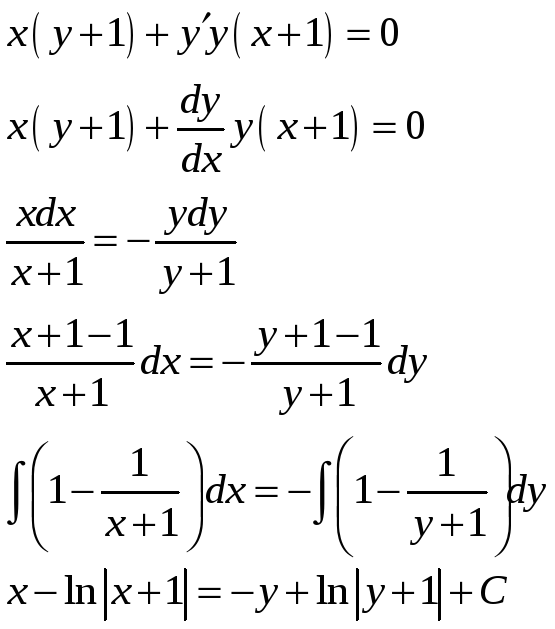
Задание 12. Найти частное решение уравнения первого порядка, удовлетворяющее следующим начальным условиям.

Решение:

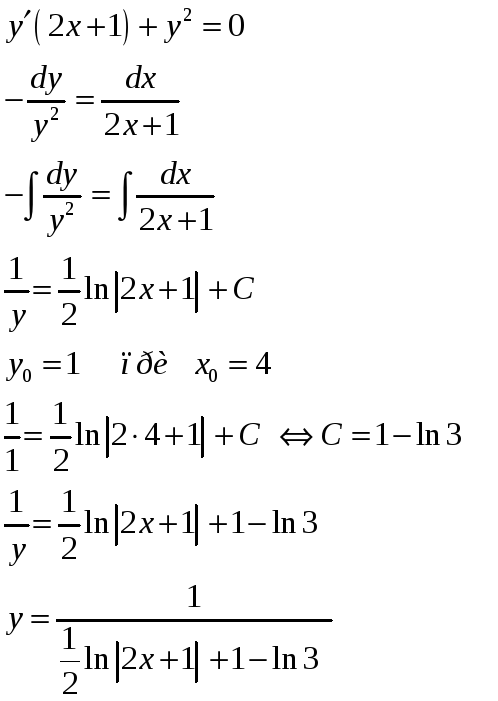
Задание 13. Найти общее решение линейного уравнения первого порядка.

Решение:

Положим y = uv, тогда

Сделаем подстановку в исходное уравнение:

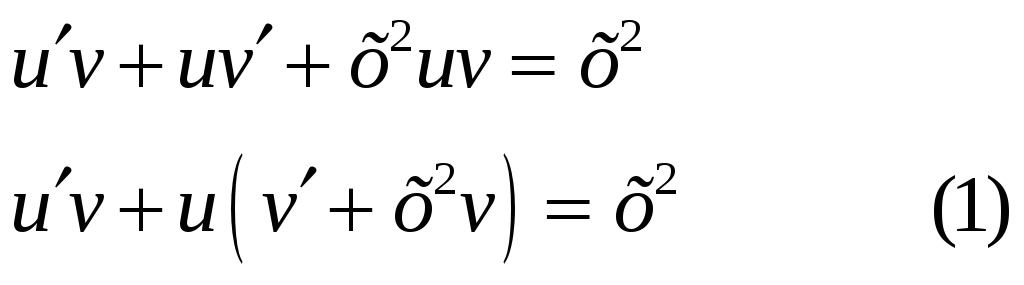
Приравняем к нулю выражение, стоящее в скобках:

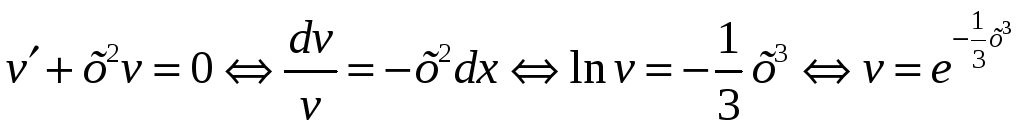
Подставим в уравнение (1):

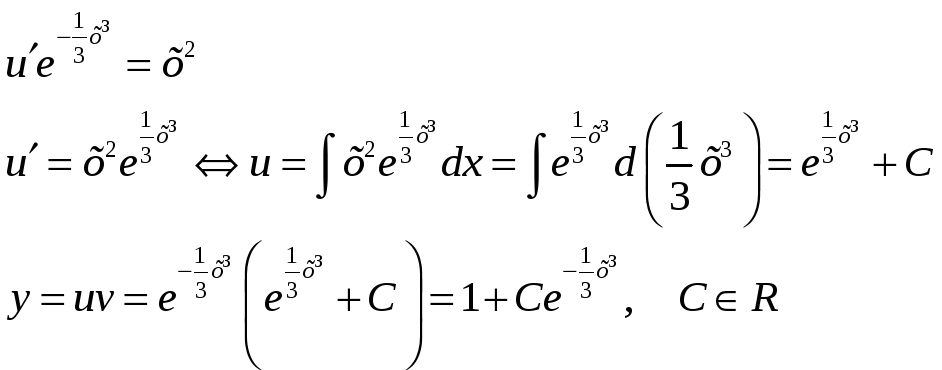
Задание 14. Найти решение линейного однородного уравнения второго порядка

Решение:

Составим и решим характеристическое уравнение:

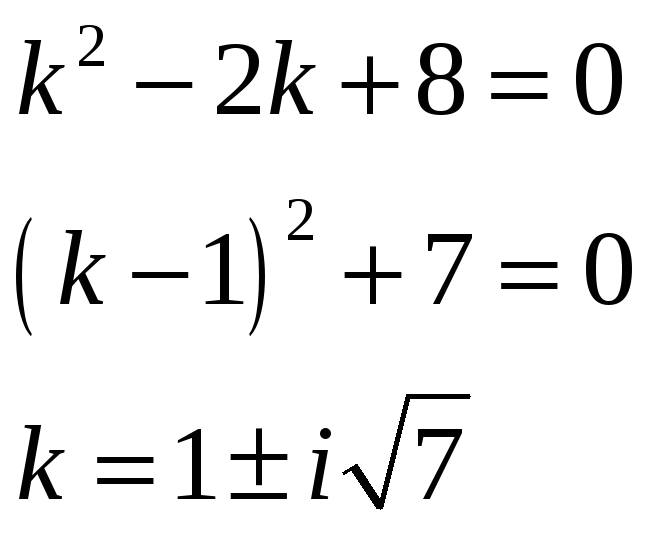
Так как получили два комплексных корня, то общее решение имеет вид: