1.1.5. Метод контурных токов

Этот метод значительно упрощает расчеты сложных цепей, так как позволяет сократить число уравнений. В соответствии с ним используется только второй закон Кирхгофа для каждого контура, и определяются контурные токи.

Общие правила расчёта:

1. выбираются независимые контуры;

2. в каждом контуре предполагается наличие контурного тока, положительное направление которого указывается стрелкой произвольно. Контурный ток – это ток, нереальный, задаваемый исключительно в целях упрощения расчетов;

3. составляются уравнения только по второму закону Кирхгофа для каждого контура, и определяются контурные токи;

4. реальные токи находятся как алгебраическая сумма контурных токов в данной ветви.

На рис. 1.19 показана сложная система, имеющая шесть ветвей (обозначим их условно индексами а, в, ав, ас, вс, с), в которых необходимо определить токи , ,,,и .

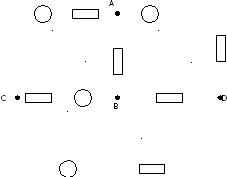
Рис. 1.19

Искомые токи в ветвях цепи должны удовлетворять системе уравнений, составленных по первому и второму законам Кирхгофа.

Число узлов в схеме равно четырем (A, B, C и D), поэтому по первому закону Кирхгофа можно было бы написать три уравнения. Но при расчёте сложных цепей методом контурных токов этого не делается, а сразу составляются оставшиеся три уравнения по второму закону Кирхгофа.

Если каждому контуру (  ) на рис. 1.19 приписывать некоторый идеализированный ток произвольно выбранного направления (I₁ , I₂ , I₃), называемый контурным током, то действительный ток в любом общем элементе, например резисторе, двух соединительных контуров можно рассматривать как алгебраическую сумму соответствующих контурных токов. Следовательно исходя из принципа наложения будем считать, что в каждом контуре протекают контурные (идеализированные) токи I₁ , I₂ , I₃ , из которых образуются действительные (реальные) токи ветвей 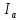, ,,,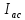и .

Составим уравнение для первого контура, обходя его в направлении собственного контурного тока и учитывая падение напряжения от всех контурных токов (естественно, смежных контуров), протекающих в резисторах первого контура. От тока I₁ будем иметь суммарное падение напряжения, равное I₁( + + ). По резистору проходит еще и контурный токI₂ смежного контура  в направлении, совпадающем с обходом контура , создающем падение напряжения I₂. По резистору протекает токI₃ так же в направлении обхода контура . Падение напряжения от этого тока равно I₃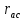. Поэтому уравнение для первого контура, составленное по второму закону Кирхгофа, имеет вид:

.

В правой части уравнения получаем 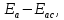т.к.совпадает с направлением обхода контура, аимеет противоположное направление.

Аналогично составим уравнение для второго и третьего контуров:

;

.

Члены уравнений ивзяты с отрицательными знаками, так как токI₃ в резисторе противоположен по направлению обхода второго контура, а токI₂ в резисторе противоположен направлению обхода третьего контура.

Сумму всех сопротивлений какого-либо контура условимся называть собственным сопротивление этого контура и обозначим двоичным индексом номера контура, например, r₁₁ – собственное сопротивление первого контура, r₂₂ – собственное сопротивление второго контура и т.д.

В нашем случае собственные сопротивления первого, второго и третьего контуров запишутся соответственно так:

;

;

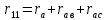Или в общем случае .

Сопротивления резисторов, которые одновременно входят в состав двух контуров, будем называть взаимными и считать их положительными, когда направления контуров токов в них совпадают, и отрицательными, когда направления токов противоположны, в частности:

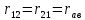– взаимное сопротивление 1…2 контуров. В резисторенаправления токовисовпадают, поэтому значение взаимного сопротивления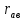пишем со знаком плюс и считаем его положительным;

– взаимное сопротивление 2…3 контуров. Токиив резисторенаправлены противоположно, соответственно значение взаимного сопротивленияберется со знаком минус и считается отрицательным;

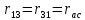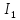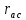– взаимное сопротивление 1…3 контуров. Токиив резисторенаправлены одинаково, и его можно считать положительным.

В общем случае можно написать , что выражает очевидные равенства взаимных сопротивлений резисторов контуровm и i.

Алгебраическую сумму всех ЭДС, действующих в каком-либо контуре, будем называть контурной ЭДС:

– контурная ЭДС первого контура.

– контурная ЭДС второго контура.

– контурная ЭДС третьего контура.

Или в общем виде для к-го контура .

В результате система уравнений для схемы на рис. 1.19 примет вид:

Для сложной цепи из n контуров может быть написана в общем виде система из n уравнений:

Полученная система уравнений является математической формулировкой метода контурных токов. Так как число контурных токов определяется количеством контуров и всегда меньше числа токов в ветвях, то применение метода контурных токов уменьшает число неизвестных величин в решаемой системе уравнений, что в значительной степени упрощает анализ сложных электрических цепей.

Приведенную сумму уравнений можно переписать в более удобном виде:

или в матричных обозначениях RI=E:

R=[r_ij] – матрица сопротивлений (квадратная матрица, т.к. число строк и столбцов равно n, т.е. n x n);

I=[I_j] – матрица токов [nx1];

E=[E_i] ­– матрица ЭДС [nx1].

Решая эти уравнения относительно любого контура тока I_k известными математическими методами, получим

где – главный определитель матрицы сопротивлений;

–алгебраическое дополнение, получаемое при вычеркивании в главном определители m-й строки и k-го стобца и умножении полученного определителя (минора) на (-1)^m+k,

,

где 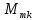– минор элемента, т.е. определитель квадратичной матрицы, полученной изR вычеркиванием m-ой строки и k-го столбца. В общем случае матрица сопротивлений запишется:

.

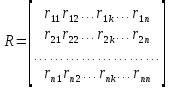Главный определитель квадратичной матрицыR находится с помощью разложения Лапласа:

где 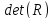– общепринятая в математике запись определителя матрицыR.

Запишем решение системы уравнений для частного примера на рис. 1.19 в общем виде:

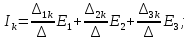
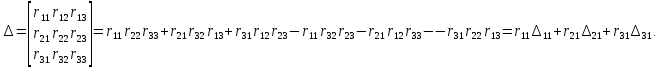
Алгебраическое дополнения определителя:

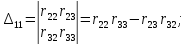
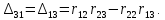
Вычислив значение контурных токов

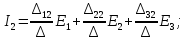
определим действительные значения токов во всех ветвях. Ток в каком-либо резисторе равен алгебраической сумме контурных токов. При этом положительным считается такой контурный ток, который в данном резисторе совпадает по направлению с результирующим током. Так, для нашего примера имеем: