1.6. Задачи для самостоятельно решения

1. Дать математическую постановку задачи линейного программирования.

2. Построить допустимую область.

Задача Т40. Джек — студент первокурсник. Он пришел к выводу, что одна только учеба без ежедневной игры в баскетбол, плохо влияет на умственное, нравственное и физическое развитие. Поэтому решил распределить свое дневное время (примерно 10 часов) для учебы и игры в баскетбол. Привлекательность игрового времени он оценивает в два раза выше, чем привлекательность времени, затраченного на учебу. Но, имея совесть и чувство долга, Джек решил, что время для игры не должно превышать время учебы. Кроме того, он заметил, что, если выполнять все учебные задания, на игру останется не более 4 часов в день. Помогите Джеку распределить время так, чтобы он получал максимальное удовольствие и от учебы, и от игры.

Глава 2. Транспортная задача

2.1. Постановка транспортной задачи

Существуют некоторые специальные классы задач линейного программирования, для решения которых можно использовать специальные методы, позволяющие ускорить процесс решения, учитывая специфику задачи. К таким задачам относятся, например, транспортные задачи (ТЗ).

Рассмотрим общую постановку транспортной задачи.

Постановка задачи. Пусть имеется пунктовпроизводства некоторого товара, ипунктовпотребления этого товара. Известны запасы товара() на каждом пункте производства, потребности() каждого пункта потребления, а также стоимости перевозок товараот каждого-того пункта производства к каждому-ому пункту потребления. Требуется составить наиболее экономичный план перевозок товара от пунктов производства к пунктам потребления.

Построим математическую модель задачи.

1). Искомые переменные задачи:

—объем перевозок от -ого пункта производства к-ому пункту потребления, где,.

План перевозок можно рассматривать, как вектор размерности.

2). Ограничения задачи.

а). Ограничения на возможности вывоза запасов из всех пунктов производства.

Суммарный объем перевозок из каждого пункта производства не может превышать объема, произведенного там товара:

, . (2.1)

b). Ограничения на потребности во всех пунктах потребления.

Суммарные перевозки в каждый пункт потребления должны полностью удовлетворять спрос на товар:

,. (2.2)

с). Ограничения на знак переменных.

Искомые переменные по условию не могут быть отрицательными:

, ,. (2.3)

3). Целевая функция минимизирует общие затраты на перевозку.

Здесь — стоимость перевозок единицы товара от-ого пункта производства к-ому пункту потребления.

Математическая постановка транспортной задачи может быть записана в виде:

(2.4)

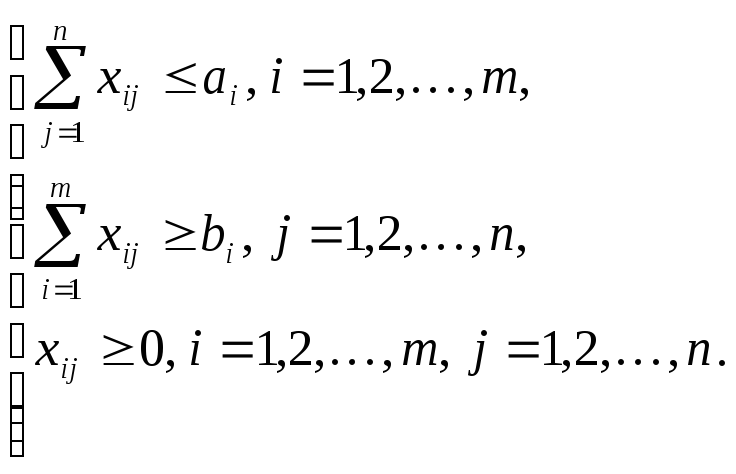(2.5)

Отметим важное свойство транспортной задачи. Для разрешимости ТЗ необходимо и достаточно, чтобы выполнялось условие баланса, при котором суммарный объем производства равен суммарному объему потребления:

. (2.6)

Транспортная задача, для которой выполнено условие баланса (2.6), называется сбалансированной или закрытой. При невыполнении условия (2.6) соответствующая задача называется несбалансированной или открытой.

Заметим, что открытая ТЗ всегда может быть сведена к закрытой путем введения фиктивного пункта производства или фиктивного пункта потребления.

Сбалансированная задача, согласно свойству (2.6) всегда имеет решение.

Рассмотрим сбалансированную задачу. При этом неравенства (2.1) и (2.2) перейдут в равенства. Математическая постановка сбалансированной задачи можно записать в форме ЗЛП:

(2.7)

(2.8)

Таким образом, ТЗ является канонической задачей линейного программирования. Ее можно решать с помощью симплекс-метода, описанного в предыдущей главе. Однако на практике для решения ТЗ, в силу ее специфических свойств, можно использовать и другие методы, в частности метод потенциалов.

Решение ТЗ методом потенциалов состоит из двух шагов:

• Нахождение начального допустимого плана.

• Нахождение оптимального решения методом потенциалов.