1.5. Двойственность в задачах линейного программирования

Каждой исходной задаче линейного программирования соответствует двойственная задача. Исходная задача называется прямой.

Приведем без доказательства ряд утверждений, связанных с двойственными задачами.

1. Если прямая и двойственная задачи имеют допустимые решения, то обе задачи имеют и оптимальные решения.

2. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций двойственных задач равны.

3. Критерий оптимальности. Пусть — целевая функция исходной задачи, а— целевая функция двойственной задачи;— допустимое решение исходной задачи, а— допустимое решение двойственной задачи. Если для этой пары двойственных задач выполняется равенство, тоиявляются оптимальными решениями соответствующих задач (справедливо и обратное утверждение).

Рассмотрим ЗЛП в общем виде. Построим задачу двойственную к исходной. При переходе к двойственно задаче, нужно соблюдать правила, которые указаны на рис. 1.9.

Правила построения двойственной задачи

Задача максимизации	z w x u	Задача минимизации
Ограничения		Переменные
=		Свободная
Переменные		Ограничения
Свободная		=

Рис. 1.9. Построение двойственной задачи

Пример 1

Задача максимизации				Задача минимизации
		z w
Ограничения				Условия на переменные
	=		Сво- бод.	свободная
Условия на переменные				Ограничения
свободная			=

В матричном виде

Ограничения				Переменные
	=		Своб.
Переменные				Ограничения
	Своб.		=	;

Задача максимизации переходит в задачу минимизации, и наоборот.

Количество переменных двойственной задачи равно количеству ограничений исходной задачи. Ограничения исходной задачи формируют условия на знак новых переменных.

Количество переменных исходной задачи равно количеству ограничений исходной задачи. Если, тогда число ограничений двойственной задачи равно. Знак исходных переменных формируют условия на знак новых ограничений.

Для нахождения допустимого плана двойственной задачи нужно найти план, который удовлетворяет всем ограничениям двойственной задачи и условиям на переменные.

При этом дополнительно используются условия дополняющей нежесткости:

а). Если для допустимого плана нестрогое неравенство в ограничениях исходной задачи выполняется как строгое, то естьили , то соответствующая переменная допустимого плана двойственной задачи равна нулю .

Если . (1.19)

Например, если , тогда(см. пример 1).

б). Если для допустимого плана некоторая переменная строго больше (меньше) нуля, , то соответствующее неравенство двойственной задачи выполняется как равенство для.

Если . (1.20)

Например, если , тогда.

Используя эти условия, получаем систему линейных уравнений для нахождения .

Задача 1. Небольшая фабрика изготовляет два вида удобрений. Продукция обоих видов поступает в оптовую продажу. Для производства удобрений используются два вида сырья A и B.

Максимально возможные суточные запасы сырья составляют 24 и 6 т соответственно. Расходы сырья A и B на 1 т на производство удобрения приведены в таблице.

Исходное сырье	Расход сырья, т на тонну		Максимально возможный запас, т
	Удобрение 1 вида	Удобрение 2 вида
А	6	4	24
В	1	2	6

Изучение рынка сбыта показало, что суточный спрос на удобрение 2 никогда не превышает спроса на удобрение 1 более чем на 1 т. Кроме того, установлено, что спрос на удобрение 1 никогда не превышает 2 т в сутки.

Оптовые цены одной тонны удобрения равны: 5 тыс. долларов для удобрения 1 и 4 тыс. долларов для удобрения 2.

Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

По исходной задаче линейного программирования постройте двойственную задачу.

Проверьте заданные планы на допустимость и оптимальность. Найдите оптимальное решение двойственной задачи. Найдите значение целевой функции для допустимых и оптимальных планов.

1. ,.

2. ,.

3. ,.

Дадим математическую постановку исходной задачи в стандартной постановке и сформулируем двойственную задачу.

Исходная задача является задачей максимизации, следовательно, двойственная будет задачей минимизации.

Исходная задача имеет 4 ограничения, следовательно, количество переменных двойственной задачи равно 4.

Количество переменных исходной задачи равно 2, следовательно двойственная задача будет иметь 2 ограничения.

Исходная задача	Двойственная задача
Задача максимизации	Задача минимизации
Исходная задача	Двойственная задача

1. Проверим план на допустимость и оптимальность.

Проверка плана на допустимость. Очевидно, что план не является допустимым, так как нарушено условие неотрицательности переменных, .

2. Проверим план .

Проверка плана на допустимость.

а). Подставим в неравенства ограничений на ресурсы.

(1)  выполняется как строгое неравенство по условию дополняющей нежесткости (1.19).

(2)  выполняется как строгое неравенство по условию дополняющей нежесткости.

(3)  выполняется как равенство,

(4)  выполняется как равенство.

ВСЕ ограничения на ресурсы выполнены.

б) Проверим условия на переменные:

строгое неравенство  соответствующее неравенство для превратиться в равенство:

;

строгое неравенство  соответствующее неравенство для превратиться в равенство:

.

ВСЕ условия на переменные выполнены.

Все ограничения на ресурсы выполнены, и все условия на переменные выполнены  план допустимый.

Проверка плана на оптимальность. На основе полученных выше равенств (подчеркнуты), сформируем систему уравнений для нахождения допустимого плана двойственной задачи.

Имеем систему уравнений:



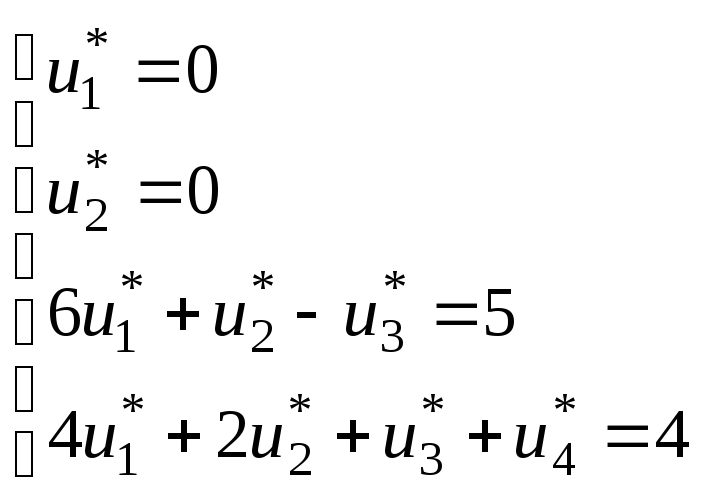
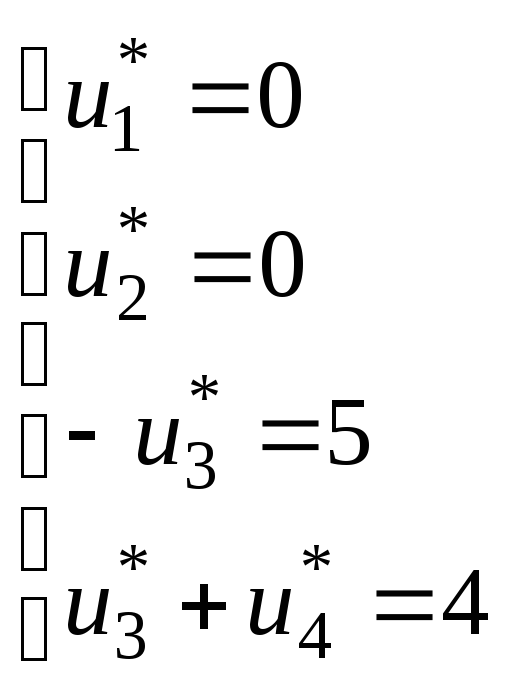
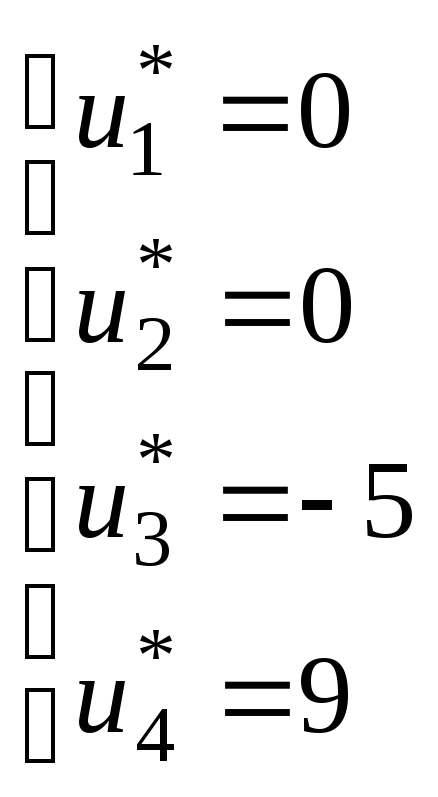
Одна из переменных отрицательна, , что не удовлетворяет условию двойственной задачи, следовательно, решение двойственной задачи не является допустимым.

Таким образом, решение исходной задачи ,допустимо, но не оптимально. Оно не удовлетворяет критерию оптимальности.

3. Проверим план .

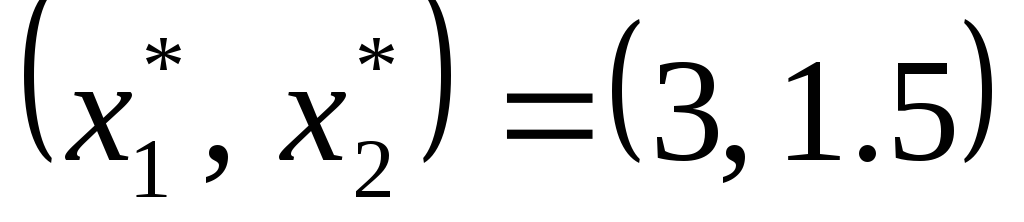Проверка плана на допустимость.

а). Подставим в неравенства ограничений на ресурсы.

(1)  выполняется как равенство;

(2)  выполняется как равенство;

(3)  выполняется как строгое неравенство по условию дополняющей нежесткости.

(4)  выполняется как строгое неравенство по условию дополняющей нежесткости.

ВСЕ ограничения на ресурсы выполнены.

б) Проверим условия на переменные:

строгое неравенство  соответствующее неравенство для превратиться в равенство:

;

строгое неравенство  соответствующее неравенство для превратиться в равенство:

.

ВСЕ условия на переменные выполнены.

Все ограничения на ресурсы выполнены, и все условия на переменные выполнены  план допустимый.

Проверка плана на оптимальность.

Рассмотрим систему уравнений:







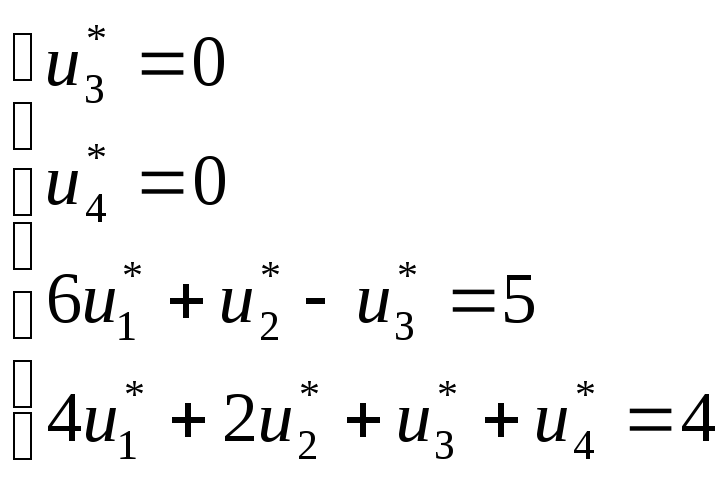
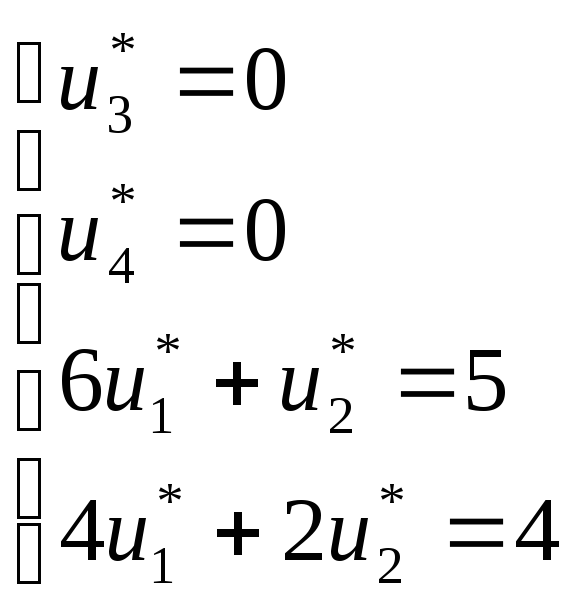
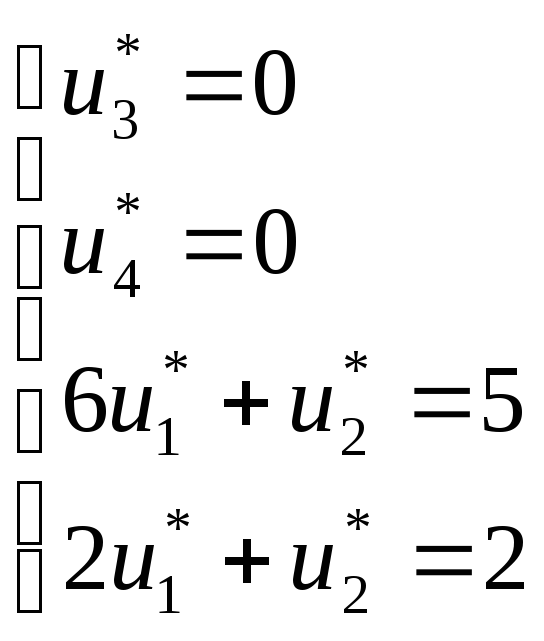
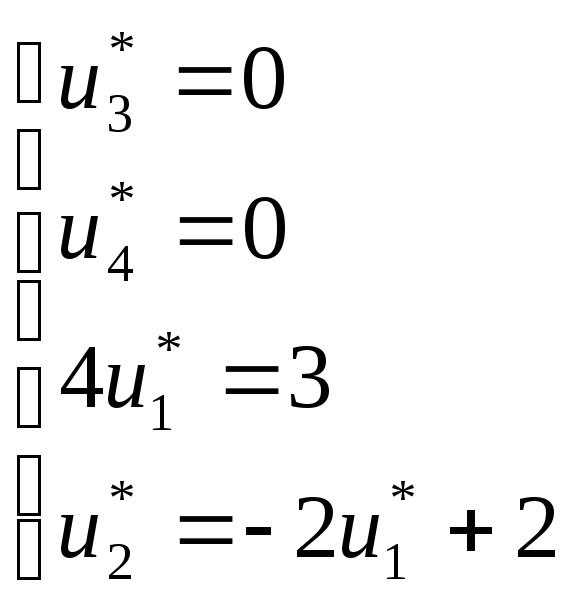
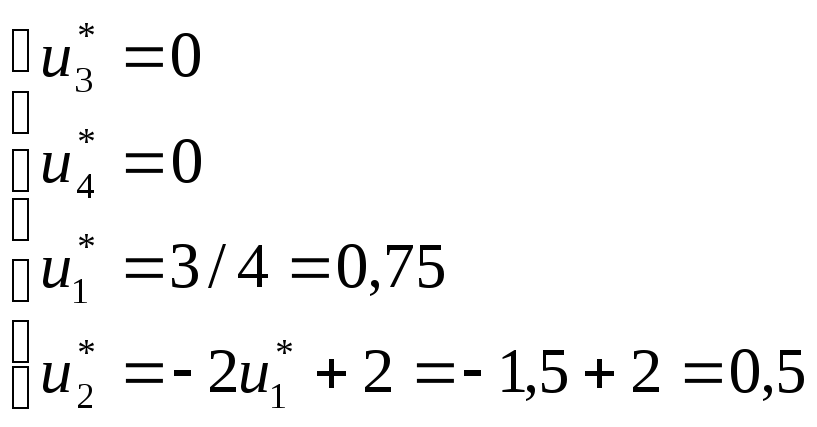
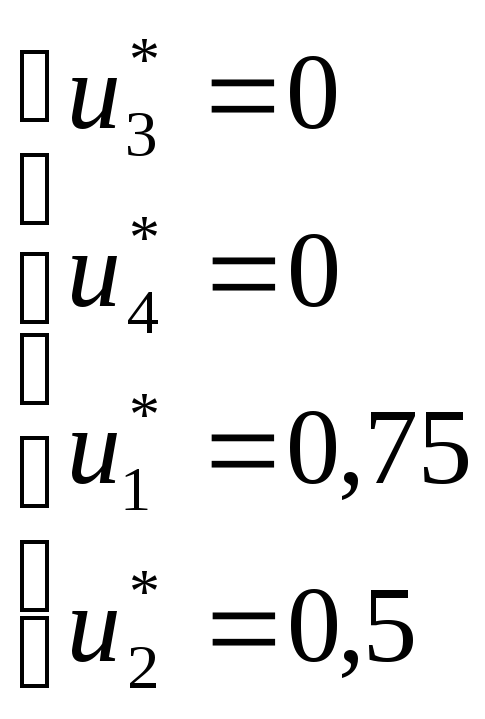
Все условия на переменные и неравенства выполнены, следовательно, решение двойственной задачи является допустимым.

Проверим критерий оптимальности. Если , гдеиявляются допустимыми планами исходной и двойственной задач соответственно, тогда эти планы являются оптимальными.

,

План является оптимальным планом исходной задачи, планявляется оптимальным планом двойственной задачи.
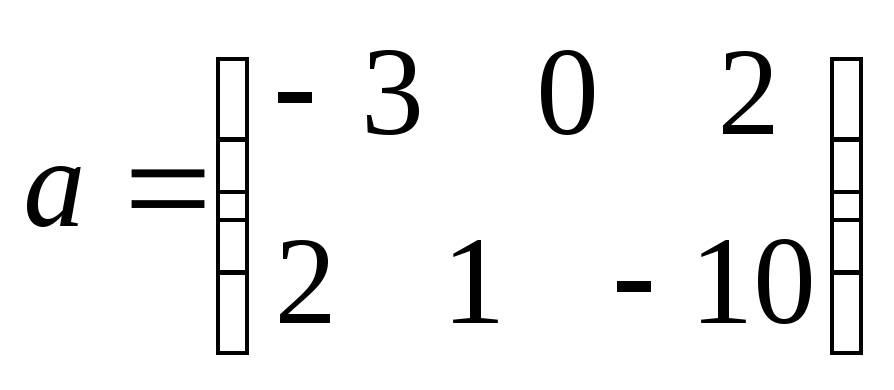
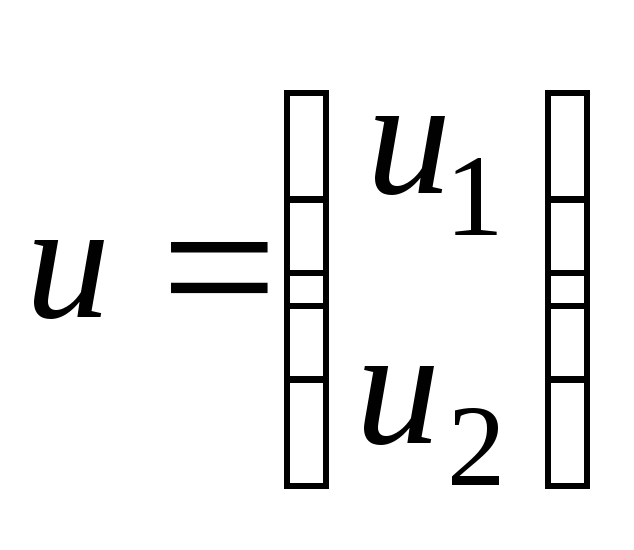