1.3 Расчет периода по способу в.Г. Сизова

Данный способ применим не только при положительных, но и при нулевой и отрицательной метацентрических высотах. Он основан на замене переменной интегрирования  новой переменной  по следующей формуле

(1.9)

Тогда , а пределам интегрирования=0 и соответствуюти. Тогда формулу для периода можно записать так

(1.10)

При любых значениях  подынтегральная функция в бесконечность не обращается . Однако при =0 имеется неопределенность типа 0/0. Применяя для ее раскрытия правило Лопиталя , получим

. (1.11)

Расчет периода качки для заданного значения угла крена по формуле (1.10) проводится в следующей последовательности:

1) Для значений переменной изменяющейся от 10 до 90 град. с шагом, вычисляются значения текущих углов крена по формуле

i=1,n ; n=9 ;

2) Для полученных значений с диаграммы динамической остойчивости снимаются значения плеч .

3) Для расчетного значения угла крена с диаграмм статической и динамической остойчивости снимаются соответствующие значения плечи.

4) Вычисление определенного интеграла в формуле (1.10 ) осуществляется по правилу трапеций с учетом раскрытой неопределенности

(1.12)

Здесь i=1,n и соотвествует значениям ;

(1.13)

1. Окончательная расчетная формула для периода будет иметь вид :

(1.14)

подставляется в радианах.

1.4 Расчет периода по способу г.Е. Павленко.

Способ Павленко применим только при положительном значении метацентрической высоты и основан на следующей замене переменной интегрирования

. (1.15)

Тогда подкоренное выражение, находящееся в знаменателе интеграла, преобразуется к виду :

(1.16)

Дифференцируя выражение (1.15), найдем

. (1.17)

С другой стороны, можно записать

. (1.18)

Приравнивая выражения (1.17) и (1.18) , найдем

. (1.19)

Определим пределы интегрирования новой переменной. При =0 имеем d=0 , и следовательно, на основании выражения (1.15) sin=0. Откуда =0.

При  . Следовательноsin=1 и =/2. Таким образом, после замены переменной интегрирования формула для периода качки преобразуется к виду

(1.20)

Входящий в (1.20) интеграл не содержит величин, обращающихся в бесконечность и для его вычисления можно применить любое правило приближенного интегрирования . При этом плечо статической остойчивости l следует рассматривать как функцию новой переменной .

Однако формула Павленко обладает тем же недостатком, что и формула Сизова. При =0, подынтегральная функция обращается в неопределенность. Используя для ее раскрытия правило Лопиталя, получим:

, (1.21)

где ho-поперечная метацентрическая высота

Порядок расчет периода качки для заданного значения угла кренапо формуле (1.20) следующий:

1. Для значений переменной изменяющейся в диапазоне от 10 до 90 град. С шагомвычислить значения плеч динамической остойчивости

, (1.22)

где -плечо динамической остойчивости, соответствующее расчетному углу крена;

2. С графика диаграммы статической остойчивости снять значения плеч 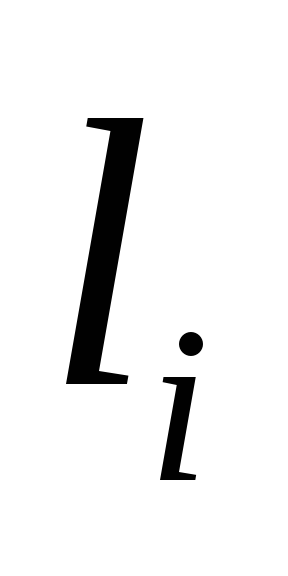, соответствующих найденным значениям(рис.1.1).

Рис.1.1 К определению плеч статической остойчивости

3. Подставляя снятые значения 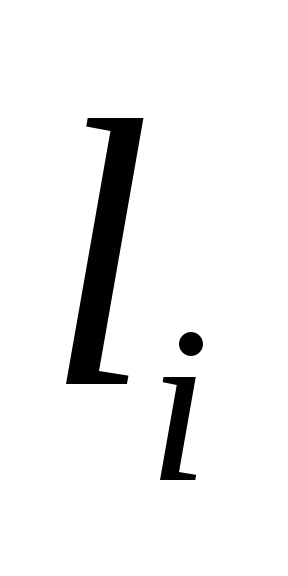в определенный интеграл , входящий в (2.20) ,вычисляем его по правилу трапеций

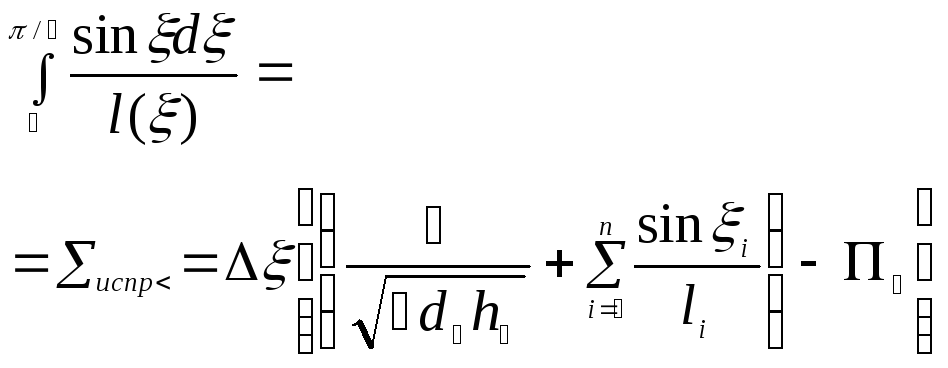; (1.23)

; (1.24)

4) Окончательная расчетная формула для периода будет иметь вид

(1.25)