
01_Основы теории горения
.pdf1
1. Основные понятия теории горения.
1. Особенности процессов горения.
Горение – сложный физико-химический процесс, при котором химическое превра-
щение сопровождается выделением энергии (главным образом в виде тепла и излучения)
и тепло- и массообменном с окружающей средой.
В основе процесса горения лежит химическая реакция, способная протекать с са-
моускорением. Причинами самоускорения могут быть:
1.Накопление тепла в системе – тепловое самоускорение
2.Накопление активных частиц – цепное самоускорение
3.Автокатализ – ускорение реакции еѐ продуктами.
Во многих случаях практически важные процессы горения подчиняются чисто фи-
зическим закономерностям, вследствие того, что при высоких температурах химическое превращение может протекать с большими скоростями и химический процесс оказывается подчинѐн чисто физическим закономерностям, таким как перенос тепла и диффузия и ими регулируется. Это означает, что химическая реакция, могущая протекать с высокой скоро-
стью, имеет ограниченную скорость и подчиняется закономерностям того или иного фи-
зического явления.
Основная особенность процессов горения состоит в том, что условия самоускоре-
ния химической реакции созданы ею самою. В кибернетике это явление носит название положительной обратной связи, то есть при малом изменении внешних условий возможен переход от стационарного режима протекания реакции с малой скоростью к режиму, к о-
гда скорость реакции возрастает в геометрической прогрессии. Подобные явления резкого изменения режима протекания реакции при малом изменении внешних условий называ-
ются критическими явлениями, а условия, при которых они наблюдаются, называются
критическими условиями.
К критическим явлениям относят:
1.Самовоспламенение
2.Зажигание
3.Концентрационные пределы распространения пламени.
Критические явления происходят не от того, что резко меняются законы природы, а
являются следствием нарушения равновесия между реагирующей системой и окружаю-
щей средой.
2
Условие самовоспламенения – невозможность теплового или диффузионного рав-
новесия с окружающей средой, условие зажигания – нарушение равновесия при заданных начальных условиях.
Второй особенностью процессов горения является их способность к распростране-
нию в пространстве. При тепловом режиме горения распространение происходит путѐм передачи тепла, при цепном или автокаталитическом – путѐм диффузии активных частиц.
2.Виды и режимы горения.
1.По агрегатному состоянию участников:
a.Горение газовых систем – гомогенное горение
b.Горение твѐрдых и жидких горючих (системы твѐрдое тело – жидкость и твѐрдое тело – газ) – гетерогенное горение
c.Горение конденсированных систем (системы твѐрдое тело – жидкость,
жидкость – жидкость, твѐрдое тело – жидкость).
2.По скорости распространения процесса:
a.Дефлаграционное горение – медленное распространение процесса (при помощи теплопроводности или диффузии)
b.Детонационное горение – быстрое распространение процесса (при по-
мощи ударной волны).
3.По аэродинамическим условиям:
a.Ламинарное горение – гладкий фронт пламени.
b.Турбулентное горение – сильно искривлѐнный фронт пламени.
Примеры различных видов горения по агрегатному состоянию участников:
Гомогенное горение:
Горение органических веществ в кислороде
CH4 (г.)+ 2O2 (г.) = CO2 (г.) + 2H2O (пар)
Горение в присутствии других газообразных окислителей
H2 (г.) + Cl2 (г.) = 2HCl (г.)
Разложение нестойких веществ (озона)
2O3(г.) = 3O2(г.)

3
Гетерогенное горение:
Горение жидкого гидразина:
N2H4(ж.) + O2(г.) = N2(г.) + 2H2O(пар)
Горение углерода:
C(тв.) + O2(г.) = CO2(г.)
Разложение нестойких веществ (ацетилена)
C2H2(г.) = 2C (тв.) + H2(г.)
Горение конденсированных систем:
KClO3(тв.) + Al(тв.) = KCl(тв.) + Al2O3(тв.) 2NH4NO3(тв.) =2N2(г.) + 4H2O(пар) + O2(г.)
3. Термодинамика процессов горения. Тепловой баланс.
Температура горения: Принято характеризовать процессы горения четырьмя тем-
пературами горения
1. |
Теоретическая |
T Теор |
- определяется по теплоте сгорания стехиометрической (т.е. |
|
г |
||||
|
|
|
||
|
отвечающей уравнению реакции) смеси с учѐтом еѐ нагрева и диссоциации |
|||
|
продуктов горения без учѐта теплообмена с окружающей средой. |
|||
2. |
Калориметрическая T калор - определяется по теплоте сгорания стехиометриче- |
|||
|
|
|
г |
|
ской смеси с начальной температурой T 0 273K без учѐта теплообмена с окру-
жающей средой.
3.Адиабатическая Tгад - определяется по теплоте сгорания смеси произвольного состава без учѐта теплообмена с окружающей средой.
4.Действительная Tгдейств - реально наблюдающаяся (измеренная) температура го-
рения.
Соотношение между различными определениями температуры горения
T теор |
T калор |
T ад |
T действ |
г |
г |
г |
г |
Тепловой баланс процессов горения основан на определении тепла, поглощѐнного
продуктами горения. Уравнение теплового баланса имеет вид:
Qпг Qр Qисх Qпот , |
(1.1) |
где Qпг -теплота, поглощенная продуктами горения, Qр - теплота химической реакции,
Qисх - теплота, поступившая из внешних источников, Qпот - тепловые потери.

|
|
|
4 |
В свою очередь тепловые потери слагаются из следующих составляющих: |
|
||
Qпот Qисп Qнед |
Qизл |
Qдисс , |
(1.2) |
Qисп - теплота испарения (плавления) вещества, Qнед - потери теплоты за счѐт неполного |
|||
сгорания (недожога), Qизл - потери на излучение, |
Qдисс |
- потери на диссоциацию продуктов |
|
горения. Практически диссоциация продуктов горения вносит заметный вклад лишь при температуре выше 20000С.
Различают высшую и низшую теплоту сгорания. В первом случае вода, как продукт горения, берѐтся в жидком виде, во втором – в парообразном. Поскольку количество вы-
делившейся теплоты зависит от количества сгоревшего вещества, различают мольную те-
плоту сгорания и удельную теплоту сгорания. Т.е. теплоту, выделившеюся при сгорании 1
моля или килограмма горючего вещества.
Для расчѐта удельной теплоты сгорания (в кДж/кг) часто используют формулу Д.И.
Менделеева
Qр 339, 4 С 1257 H 108,9 O N S 25 9 H W , |
(1.3) |
где X - содержание элемента в составе горючего в %(масс.), W – влажность.
Общий подход к вычислению теплот реакций основан на химической термодина-
мике. Условимся считать положительными теплоту, полученную системой и работу, со-
вершѐнную системой. Тогда из первого начала термодинамики (закона сохранения энер-
гии) следует |
|
|
|
Q |
U |
W , |
(1.4) |
где Q – теплота, полученная системой, U - изменение внутренней энергии, W – работа, |
|||
совершѐнная системой. Для бесконечно малых изменений имеем |
|
||
Q |
dU |
W . |
(1.5) |
dU - полный дифференциал внутренней энергии (не зависит от пути протекания |
|||
процесса) Q, W - бесконечно малые количества теплоты и работы, которые, |
в общем |
||
случае, зависят от пути перехода системы из одного состояния в другое. |
|
||
Пусть система совершает только механическую работу расширения. |
|
||
W |
pdV . |
(1.6) |
|
Подставляя (1.6) в (1.5) получим |
|
|
|
Q |
dU |
pdV |
(1.7) |
При изохорном процессе V=const dV=0 и интегрируя (1.7) получим |
|
||
Qv |
|
U , |
(1.8) |
в изобарном процессе p=const интегрирование (1.7) и простые преобразования дают
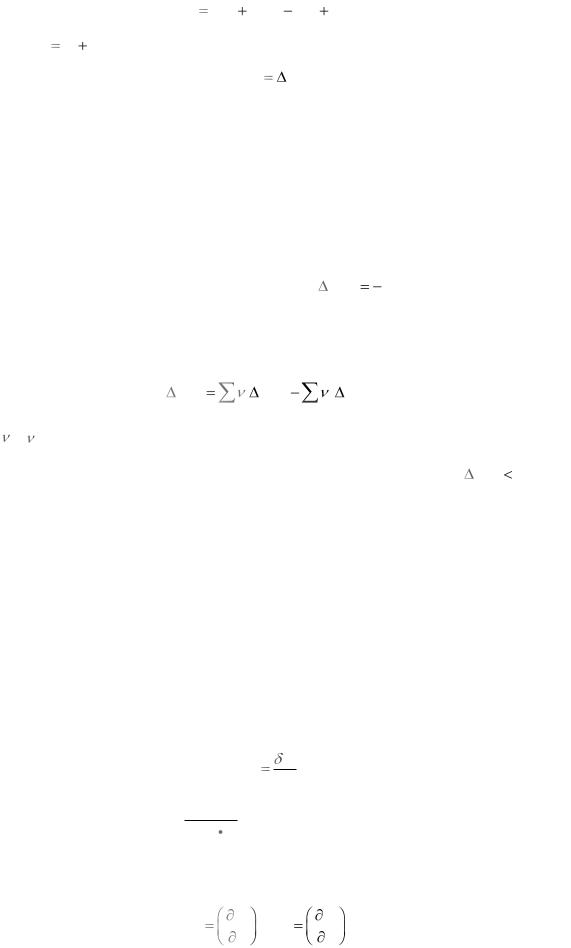
|
|
5 |
Qp U2 pV2 |
U1 pV1 . |
(1.9) |
Величину H U pV называют энтальпией (теплосодержанием) т.о. |
|
|
Qp |
H |
(1.10) |
Из (1.8) и (1.10) следует, что в изохорном и изобарном процессах теплота приобретает свойства функции состояния, т.е. не зависит от пути протекания процесса. Это положение получило название закона Г.И. Гесса. Начальным и конечным состоянием химической ре-
акции являются исходные вещества и продукты реакции. Энтальпии простых веществ, ус-
тойчивых при стандартных условиях (298К и 0,10113 МПа) приняты равными нулю. Для сложных веществ рассматривают изменение энтальпии при их образовании из элементов.
|
|
|
Ca(тв.) + С(тв.) + 1,5O2 = CaCO3 |
|
H 0 |
1206 |
кДж |
. |
|
|
|
||||
|
|
|
f |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
моль |
|
|
|
|
|
Правило вычисления теплот реакции по энтальпиям образовния веществ следует из |
||||||||||||||
закона Гесса. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
N |
|
M |
|
|
|
|
|
|
|
|
|
|
|
r |
H 0 |
i f |
H 0 |
j |
f |
H |
0 , |
|
|
|
|
(1.11) |
|
|
|
|
i |
|
j |
|
|
|
||||||
|
|
|
|
|
i |
|
j |
|
|
|
|
|
|
|
|
здесь |
i |
j |
стехиометрические коэффициенты продуктов реакции и исходных веществ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
соответственно. При этом в соответствии с соглашением о знаках если |
r |
H 0 |
0 то реак- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ция экзотермическая (выделяет тепло).
4.Теплоёмкость. Зависимость теплового эффекта реакции от температу-
ры.
Теплоѐмкостью – называют количество теплоты, необходимое для нагрева едини-
цы массы вещества на 1 К. Различают удельную и молярную теплоѐмкости, т.е. количество теплоты, необходимое для нагрева 1 кг. Или 1 моля вещества на 1 К.
Истинная молярная теплоѐмкость определяется следующим образом
Q
С (1.12) dT
Дж
где С – молярная теплоѐмкость, моль К .
Для теплоѐмкостей при постоянном объѐме и давлении (изохорной и изобарной) с
учѐтом (1.8) и (1.10) получаем
Cv |
U |
;Cp |
H |
. |
(1.13) |
|
|
|
|||||
T |
T |
|||||
|
V |
p |
|

6
Рассмотрим зависимость теплоты процесса от температуры при постоянном объѐме или давлении. Учитывая уравнения (1.13) получим
H
T p
H |
C |
; |
U |
U |
C |
,1 |
(1.14) |
|
|
|
|
|
|||||
|
|
|
|
|||||
T |
p |
|
T V |
T |
V |
|
|
|
p |
|
V |
|
|
||||
Уравнения (1.14) называют уравнениями Кирхгоффа.
Изменение теплоѐмкости в ходе реакции определяется выражением
N |
|
M |
|
Cp |
iCp,i (прод) |
jCp, j (исх) , |
(1.15) |
i |
|
j |
|
т.е. разностью между суммой теплоѐмкостей продуктов реакции и исходных веществ.
Из уравнения (1.14) следует, что если изменение теплоѐмкости в ходе реакции от-
рицательно (т.е. теплоѐмкость продуктов меньше теплоѐмкости исходных веществ) то и тепловой эффект реакции становится более отрицательным, реакция становится более эк-
зотермичной.
Сp |
0; |
d H |
0 . |
(1.16) |
|
dT |
|||||
|
|
|
|
||
Для вычисления теплового эффекта процесса при T2 (p=const) уравнение Кирхгоф- |
|||||
фа надо проинтегрировать. |
|
|
|
|
|
|
|
T2 |
|
|
|
HT |
HT |
Cp dT , |
(1.17) |
||
2 |
1 |
|
|
||
|
|
T1 |
|
|
|
Нужно иметь ввиду, что в интервале температур Т1 - Т2 |
не должно быть фазовых перехо- |
||||
дов веществ. |
|
|
|
|
|
Обычно Т1 выбирают 298К, тогда |
HT |
r H 0 - тепловой эффект реакции в стан- |
|||
|
1 |
|
|
||
дартных условиях, вычисляемый по (1.11).
Теплоѐмкость реальных веществ сложным образом зависит от температуры, поэто-
му для интегрирования уравнения Кирхгоффа используют следующие приближения: |
|
|||
1. |
Нулевое – теплоѐмкость продуктов равна теплоѐмкости исходных веществ, |
|||
|
т.е. Cp 0 и тепловой эффект реакции не зависит от температуры. |
|
||
2. |
Первого порядка - Cp |
a const , тогда |
|
|
|
HT |
HT |
a T2 T1 |
(1.18) |
|
2 |
1 |
|
|
1 Операторы |
и обладают свойством коммутативности, т.е. |
x |
x . Действительно, |
|
x2 x1 |
x2 |
x1 . |
|
|
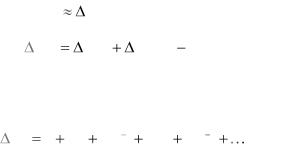
7
Или принимая во внимание a Cp298
H |
T r |
H 0 C |
p |
T 298 |
(1.19) |
|
|
2 |
|
||
|
2 |
|
|
|
|
3.Второго порядка. Зависимость теплоѐмкости от температуры аппроксими-
руется степенным рядом
Cp a bT b'T 1 cT 2 c'T 2 |
(1.20) |
