20. Направление выпуклости графика функции. Достаточное условие выпуклости

графика функции.

Направление выпуклости графика функции.

 Опр. 1. График функции имеет на интервалевыпуклость, направленную вниз, если он расположен не ниже любой касательной, проведённой на этом интервале.

 Опр.2. График функции имеет на интервалевыпуклость, направленную вверх, если он расположен не выше любой касательной, проведённой на этом интервале.

 Теор.1. (Достаточное условие выпуклости графика функции). Если функция имеет на интервалевторую производную, и() для, то её график имеет на этом интервале выпуклость, направленную вниз (вверх).

 Док-во. Пусть, для определённости, на. Пусть с - произвольная точка, докажем, что график функции лежит выше касательной, проведённой к нему в точке. Уравнение касательной:(- текущая точка касательной).

По формуле Тейлора 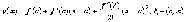. Вычитая из этого равенства предыдущее, получимна, т.е. точка графика функции действительно лежит выше точки графика касательной.

 Аналогично рассматривается случай на.

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );

если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .

21. Точки перегиба. Необходимое условие существования перегиба. Достаточное

условие существования перегиба.

Точка перегиба функции это точка ,в которой существует касательная к графику и существует такая окрестность точки , в которой график имеет разные направления выпуклости.

Необходимые условия наличия перегиба 

 либо не существует.

Достаточные условия наличия перегиба 

1. Если меняет знак при переходе через точкуx₀, то x₀ - точка перегиба.

2. Если 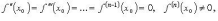то приn четном x₀ - точка перегиба, при n нечетном x₀ не является точкой перегиба.

22. Понятие о многочлене Тейлора. Формула Тейлора для функции одной переменной (без доказательства). Формула Маклорена для функций ,,.

Рассмотрим многочлен -й степени

Его можно представить в виде суммы степеней , взятых с некоторыми коэффициентами. Продифференцируем егораз по переменной, а затем найдем значения многочлена и его производных в точке:

Таким образом, получаем, что

Полученное выражение называется формулой Маклорена для многочлена 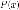степени.

Рассуждая аналогично, можно разложить многочлен по степеням разности, где- любое число. В этом случае будем иметь:

Это выражение называется формулой Тейлора для многочлена в окрестности точки.

Разложение функции e^x

Так как (e^x)' = e^x, то производная любого порядка функции e^x равна e^x. При x = 0 функцияe^x и ее производные любого порядка равны одному. Таким образом, формула Маклорена для функции e^x имеет вид

Отметим, что для любого вещественного числа x остаточный член

В самом деле, если x – фиксированное число, то, начиная с некоторого положительного целого числа N, для любого n > N имеем

Следовательно

так как q < 1, а величина является постоянной при любомn. Таким образом, значения функции e^x могут быть найдены приближенно по формуле:

Разложение функции cos x

Находим последовательно производные от f(x) = cos x.

При x = 0 получаем

Следовательно, формула Маклорена для функции cos x имеет вид

Так как , то

для любого фиксированного вещественного числа x. Таким образом, значения функции cosx могут быть найдены приближенно по формуле

Разложение функции sin x

Формула Маклорена для функции sin x находится аналогично формуле Маклорена для cos x

Причем

для любого фиксированного вещественного числа x.