11. Дифференцируемые функции. Необходимое и достаточное условие

дифференцируемости. Дифференциал. Непрерывность дифференцируемой

функции.

1) Дифференци́руемаяфу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.

2) Для того, чтобы функция f(x) была дифференцируема в точке x₀ необходимо и достаточно, чтобы у нее существовала производная в этой точке.

При этом

Δy = f(x0+Δx)-f(x0) = f '(x0)Δx+α(Δx)Δx,

где α(Δx) - бесконечно малая функция, при Δx→0.

3) Дифференциа́л (от лат. differentia — разность, различие) — линейная часть приращения функции.

4) Теорема 1. Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция fнепрерывна на (a, b).

Доказательство

Возьмем произвольное фиксированное число x (a,b).

По условию теоремы

Следовательно, в малой окрестности числа x₀ можно определить функцию α = α(Δx), стремящуюся к нулю при такую, что

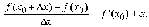
Но тогда и, следовательно, функция f непрерывна приx = x₀. Так как число x₀ – произвольное, то функция fнепрерывна на всем интервале (a, b).

Теорема доказана.

12. Производная функции в точке. Правила дифференцирования суммы,

произведения и частного.

1) Определение. Производной функции называетсяпредел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

.

2) Правила дифференцирования суммы, произведения и частного

Теорема Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы: 1) (u±v)/=u/±v/ , 2) (u·v)/=u/v+v/u , 3) (vu)=v2u/v−v/u .

Доказательство Из определения производной:

(u±v)/=limΔx→0Δx[u(x+Δx)±v(x+Δx)]−[u(x)±v(x)]= =limΔx→0Δx[u(x+Δx)−u(x)]±[v(x+Δx)−v(x)]=  .    

=limΔx→0Δxu(x+Δx)−u(x)±limΔx→0Δxv(x+Δx)−v(x)=u/±v/

(u·v)/=limΔx→0Δxu(x+Δx)·v(x+Δx)−u(x)·v(x)±v(x+Δx)·v(x)= limΔx→0Δxu(x+Δx)[v(x+Δx)−v(x)]+      

+limΔx→0Δxv(x)[u(x+Δx)−u(x)]=uv/+vu/.

(vu)/=limΔx→0Δxv(x+Δx)u(x+Δx)−v(x)u(x)=limΔx→0Δx·v(x+Δx)·v(x)u(x+Δx)·v(x)−u(x)·v(x+Δx)±u(x)·v(x)=v2u/v−v/u.

Теорема доказана.

13. Теорема Ферма.

Для любого натурального числа уравнение

не имеет натуральных решений ,и.

14. Теорема Ролля

  Теорема. Пусть функция  дифференцируема в открытом промежутке, на концах этого промежутка сохраняет непрерывность и принимает одинаковые значения:. Тогда существует точка, в которой производная функцииравна нулю:.

Рис. 3. Теорема Ролляустанавливает условия существования хотя бы одной точкиc, в которой касательная к графику функции параллельна оси 0x. Таких точек может быть несколько.

      Доказательство. Если  в промежутке, тово всех точках этого промежутка. Иначе наибольшее значениеM  функции  превышает ее наименьшее значениеm  в промежутке  . Поскольку на концах этого промежутка функцияпринимает одинаковые значения, то по крайней мере одно из значений,M  или  m, достигается во внутренней точке  c  промежутка  . Тогда по теореме Ферма.