
- •1. Окрестность точки на числовой прямой. Предел функции в точке. Предел в бесконечно удаленной точке. Геометрическая интерпретация предела.
- •2. Односторонние пределы. Теорема о существовании предела функции в точке.
- •3. Непрерывность функции в точке. Точки разрыва. Классификация точек разрыва.
- •3) Классификация точек разрыва функции
- •4. Предел функции в точке. Единственность предела.
- •5. Бесконечно малые функции в точке. Теоремы о бесконечно малых.
- •6. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •7. Теорема о предельном переходе под знаком неравенства. Теорема о сжатой
- •8. Теорема о сохранении знака функции. Теорема о связи функции, имеющей
- •9. Односторонняя непрерывность. Непрерывность функции на отрезке. Теоремы
- •10. Производная функция в точке. Геометрическая и механическая интерпретация.
- •11. Дифференцируемые функции. Необходимое и достаточное условие
- •12. Производная функции в точке. Правила дифференцирования суммы,
- •13. Теорема Ферма.
- •14. Теорема Ролля
- •15. Теорема Лагранжа
- •16. Теорема Коши
- •17. Правило Лопиталя
- •18. Экстремумы функции одной переменной. Необходимое условие экстремума.
- •19. Экстремумы функции одной переменной. Достаточное условие экстремума.
- •20. Направление выпуклости графика функции. Достаточное условие выпуклости
- •21. Точки перегиба. Необходимое условие существования перегиба. Достаточное
- •22. Понятие о многочлене Тейлора. Формула Тейлора для функции одной переменной (без доказательства). Формула Маклорена для функций ,,.
- •23. Первообразная и неопределенный интеграл. Их свойства.
- •24. Первообразная и неопределенный интеграл. Методы вычисления
- •Интегрирование методом подстановки.
- •Интегрирование по частям.
- •25. Дробно-рациональная функция. Типы простейших алгебраических дробей и их интегрирование.
- •26. Интегральная сумма Римана. Определенный интеграл Римана. Интегрируемые функции. Геометрическая интерпретация определенного интеграла.
6. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
1)
Пусть  и
и —
бесконечно малые при
—
бесконечно малые при .
1.
Если
.
1.
Если ,
то говорят, что
,
то говорят, что являетсябесконечно
малой высшего порядка по
сравнению с
являетсябесконечно
малой высшего порядка по
сравнению с  .
В этом случае пишут
.
В этом случае пишут .
2.
Если
.
2.
Если ,
где
,
где —число,
отличное от нуля, то говорят,
что
—число,
отличное от нуля, то говорят,
что и
и —бесконечно
малые одного и того же порядка.
В часности, если
—бесконечно
малые одного и того же порядка.
В часности, если  ,
то бесконечно малые
,
то бесконечно малые и
и называются
эквивалентными. Запись
называются
эквивалентными. Запись ~
~ означает,
что
означает,
что и
и —эквивалентные
бесконечно малые.
Если
—эквивалентные
бесконечно малые.
Если ,
то это означает, что
,
то это означает, что .
Таким образом,
.
Таким образом, является
бесконечно малой высшего порядка по
сравнению с
является
бесконечно малой высшего порядка по
сравнению с ,
т. е.
,
т. е. 3.
Если
3.
Если и
и —бесконечно
малые одного и того же порядка, причем
—бесконечно
малые одного и того же порядка, причем ,
то говорят, что бесконечно малая
,
то говорят, что бесконечно малая имеет
порядок
имеет
порядок по
сравнению с
по
сравнению с .
Отметим
некоторые свойства бесконечно малых
величин:
1o. Произведение
двух бесконечно малых есть бесконечно
малая высшего порядка по сравнению с
сомножителями,
т. е. если
.
Отметим
некоторые свойства бесконечно малых
величин:
1o. Произведение
двух бесконечно малых есть бесконечно
малая высшего порядка по сравнению с
сомножителями,
т. е. если  ,
то
,
то и
и .
2o. Бесконечно
малые
.
2o. Бесконечно
малые  и
и эквивалентны
тогда и только тогда, когда их
разность
эквивалентны
тогда и только тогда, когда их
разность является
бесконечно малой высшего порядка по
сравнению с
является
бесконечно малой высшего порядка по
сравнению с и
и ,
т. е. если
,
т. е. если  ,
,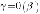 .
3o. Если
отношение двух бесконечно малых имеет
предел, то этот предел не изменится при
замене каждой из бесконечно малых
эквивалентной ей бесконечно малой,
т.е. если
.
3o. Если
отношение двух бесконечно малых имеет
предел, то этот предел не изменится при
замене каждой из бесконечно малых
эквивалентной ей бесконечно малой,
т.е. если
 ,
, ~
~ ,
,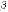 ~
~ ,
то
,
то .
.
2)
Б.м.
функции и
и называютсяэквивалентнымиилиравносильными
б.м. одного порядка при
называютсяэквивалентнымиилиравносильными
б.м. одного порядка при ,
если
,
если
Обозначают: при
при .
.
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть  -
бесконечно малая при
-
бесконечно малая при 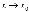 .
.

7. Теорема о предельном переходе под знаком неравенства. Теорема о сжатой
переменной (формулировка).
1) ТЕОРЕМА: (о предельном переходе в неравенстве.).
Пусть
при всех n выполняется неравенство  ,и
переменные
,и
переменные
 и
имеют пределы:
и
имеют пределы:
 ;
;
Тогда: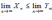 ,
т. е.
,
т. е. .
.
Теорема означает, что в неравенстве можно переходить к пределам, сохраняя знак неравенства.
Доказательство:
Предположим,
что 

Выделим
вокруг точек  и
и столь
малыеE –
окрестности, чтобы они не пересекались.
столь
малыеE –
окрестности, чтобы они не пересекались.
По
определению предела, начиная с некоторого
номера n, переменные  и
и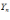 попадут
в своиE –
окрестности предельных точек.
попадут
в своиE –
окрестности предельных точек.
Это
означает, что
 ,
начиная с некоторого номера n, что
противоречит условию. Противоречие
доказывает теорему, ч. т. д.
,
начиная с некоторого номера n, что
противоречит условию. Противоречие
доказывает теорему, ч. т. д.
Замечание:
Если
при всех n выполняется 
 (строго),
то гарантировать строгого неравенства
в пределе нельзя (в общем случае),
гарантируется лишь нестрогое неравенство.
(строго),
то гарантировать строгого неравенства
в пределе нельзя (в общем случае),
гарантируется лишь нестрогое неравенство.
2) ТЕОРЕМА: (о сжатой переменной).
Пусть,
начиная с некоторого  ,
выполняются неравенства
,
выполняются неравенства ,
причем крайние переменные имеют
одинаковый конечный предел
,
причем крайние переменные имеют
одинаковый конечный предел ,
тогда переменная
,
тогда переменная также
имеет предел, причем тот же самый.
также
имеет предел, причем тот же самый.
8. Теорема о сохранении знака функции. Теорема о связи функции, имеющей
конечный предел, с бесконечно малой.
1) Теорема.
(Теорема о сохранении знака непрерывной
функции). Если
 ,
, ,
то
,
то .
.
Доказательство.
Достаточно доказать, что если
 ,
то и
,
то и .
Действительно, взяв
.
Действительно, взяв получаем по определению непрерывности
окрестность
получаем по определению непрерывности
окрестность
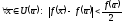
 .
.
2)
Теорема Для
того, чтобы функция
 имела предел в точкеaравный
А, необходимо и достаточно, чтобы имело
место представление :
имела предел в точкеaравный
А, необходимо и достаточно, чтобы имело
место представление : ,
где
,
где -
бесконечно малая функция в точкеa
.
-
бесконечно малая функция в точкеa
.
ДОК.
(1) Если
 ,
то функция
,
то функция б.м.ф.
Действительно,
б.м.ф.
Действительно,
 (2)
(2)

 .
.
