
- •1. Окрестность точки на числовой прямой. Предел функции в точке. Предел в бесконечно удаленной точке. Геометрическая интерпретация предела.
- •2. Односторонние пределы. Теорема о существовании предела функции в точке.
- •3. Непрерывность функции в точке. Точки разрыва. Классификация точек разрыва.
- •3) Классификация точек разрыва функции
- •4. Предел функции в точке. Единственность предела.
- •5. Бесконечно малые функции в точке. Теоремы о бесконечно малых.
- •6. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •7. Теорема о предельном переходе под знаком неравенства. Теорема о сжатой
- •8. Теорема о сохранении знака функции. Теорема о связи функции, имеющей
- •9. Односторонняя непрерывность. Непрерывность функции на отрезке. Теоремы
- •10. Производная функция в точке. Геометрическая и механическая интерпретация.
- •11. Дифференцируемые функции. Необходимое и достаточное условие
- •12. Производная функции в точке. Правила дифференцирования суммы,
- •13. Теорема Ферма.
- •14. Теорема Ролля
- •15. Теорема Лагранжа
- •16. Теорема Коши
- •17. Правило Лопиталя
- •18. Экстремумы функции одной переменной. Необходимое условие экстремума.
- •19. Экстремумы функции одной переменной. Достаточное условие экстремума.
- •20. Направление выпуклости графика функции. Достаточное условие выпуклости
- •21. Точки перегиба. Необходимое условие существования перегиба. Достаточное
- •22. Понятие о многочлене Тейлора. Формула Тейлора для функции одной переменной (без доказательства). Формула Маклорена для функций ,,.
- •23. Первообразная и неопределенный интеграл. Их свойства.
- •24. Первообразная и неопределенный интеграл. Методы вычисления
- •Интегрирование методом подстановки.
- •Интегрирование по частям.
- •25. Дробно-рациональная функция. Типы простейших алгебраических дробей и их интегрирование.
- •26. Интегральная сумма Римана. Определенный интеграл Римана. Интегрируемые функции. Геометрическая интерпретация определенного интеграла.
4. Предел функции в точке. Единственность предела.
1)Число  называетсяпределом
функции
называетсяпределом
функции  в
точке
в
точке  ,
если для
,
если для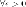
 такое,
что для
такое,
что для из
того, что
из
того, что следует,
что
следует,
что :
: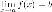 или
или при
при .
.
2) Теорема о единственности предела
Формулировка:
Если
функция 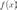 в
точке
в
точке имеет
предел, то этот предел единственный.
имеет
предел, то этот предел единственный.
Доказательство:
Докажем
методом от противного. Предположим,
что  ,
, ,
, .
Возьмём
.
Возьмём ,
по определению и свойству окрестности
найдётся такая проколотая
,
по определению и свойству окрестности
найдётся такая проколотая -окрестность
точки
-окрестность
точки (
( ),
в которой одновременно будут выполнятся
неравенства
),
в которой одновременно будут выполнятся
неравенства ,
, ,
тогда в точках этой же окрестности
,
тогда в точках этой же окрестности . Получили
противоречие
. Получили
противоречие .
Отсюда, функция
.
Отсюда, функция в
точке
в
точке имеет
единственный предел.
имеет
единственный предел.
5. Бесконечно малые функции в точке. Теоремы о бесконечно малых.
1)
Функция  называетсябесконечно
малой функцией (б.м.ф.) при
называетсябесконечно
малой функцией (б.м.ф.) при  (или
в точке
(или
в точке ),
если
),
если
2)Теорема 1. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.
Доказательство. Пусть  –
бесконечно малая последовательность.
Это означает, что для любого положительного
числа
–
бесконечно малая последовательность.
Это означает, что для любого положительного
числа существует
такой номерN,
что для всех номеров
существует
такой номерN,
что для всех номеров  выполняется
условие
выполняется
условие ,
гдеС –
любое действительное число. Тогда
,
гдеС –
любое действительное число. Тогда 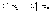 <
<
< 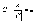 ,
а это и означает, что последовательность
,
а это и означает, что последовательность –
бесконечно малая.
–
бесконечно малая.
Теорема 2. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство. Пусть  и
и –
бесконечно малые последовательности.
Это означает, что для любого
числа
–
бесконечно малые последовательности.
Это означает, что для любого
числа существуют
такие номера
существуют
такие номера и
и ,
что для всех номеров
,
что для всех номеров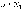 и
для всех номеров
и
для всех номеров выполняются
условия
выполняются
условия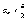 и
и соответственно.
Тогда для всех номеров
соответственно.
Тогда для всех номеров выполняется
условие
выполняется
условие
 ,
а это и означает, что последовательность
,
а это и означает, что последовательность –
бесконечно малая.
–
бесконечно малая.
Следствие 1. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Следствие 2. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 3. Бесконечно малая последовательность ограничена.
Доказательство. Пусть  –
бесконечно малая последовательность,ε>0
– некоторое
число, а N
– номер,
начиная с которого выполняется условие
–
бесконечно малая последовательность,ε>0
– некоторое
число, а N
– номер,
начиная с которого выполняется условие  .
Обозначим черезМ наибольшее
из следующих чисел
.
Обозначим черезМ наибольшее
из следующих чисел  .
Очевидно, что
.
Очевидно, что для
любого номераn,
а это и означает, что последовательность
{
для
любого номераn,
а это и означает, что последовательность
{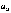 } –
ограничена.
} –
ограничена.
Теорема 4. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
Доказательство. Пусть  –
ограниченная, а
–
ограниченная, а –
бесконечно малая последовательности.
Это означает, что существует числоМ>0
такое, что для любого номера n выполняется
–
бесконечно малая последовательности.
Это означает, что существует числоМ>0
такое, что для любого номера n выполняется  ,
и для любого числа
,
и для любого числа существует
номерN такой,
что для всех номеров
существует
номерN такой,
что для всех номеров  выполняется
выполняется .
Тогда для всех номеров
.
Тогда для всех номеров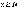 и
любогоε>0
выполняется
и
любогоε>0
выполняется  ,
а это и означает, что последовательность
,
а это и означает, что последовательность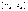 –
бесконечно малая.
–
бесконечно малая.
Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема
5. Если
элементы бесконечно малой
последовательности  равны
одному и тому же числуС,
то С=0.
равны
одному и тому же числуС,
то С=0.
Доказательство. Предположим,
что 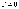 .
Для
.
Для существует
такой номерN,
что для всех номеров
существует
такой номерN,
что для всех номеров  выполняется
выполняется .
Так как
.
Так как ,
а
,
а ,
то последнее неравенство имеет вид
,
то последнее неравенство имеет вид ,
откуда
,
откуда .
Полученное противоречие показывает,
что предположение
.
Полученное противоречие показывает,
что предположение неверно,
следовательно,
неверно,
следовательно, .
.
Теорема
6. Если  –
бесконечно большая последовательность
то, начиная с некоторого номера n,
определена последовательность
–
бесконечно большая последовательность
то, начиная с некоторого номера n,
определена последовательность ,
которая является бесконечно малой. Если
не все элементы бесконечно малой
последовательности
,
которая является бесконечно малой. Если
не все элементы бесконечно малой
последовательности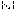 равны
нулю, то последовательность
равны
нулю, то последовательность бесконечно
большая.
бесконечно
большая.
Доказательство. Пусть –
бесконечно большая последовательность.
Это означает, что для любого положительного
числаМ можно
указать такой номер N,
что для всех номеров
–
бесконечно большая последовательность.
Это означает, что для любого положительного
числаМ можно
указать такой номер N,
что для всех номеров  выполняется
выполняется .
А это означает, что при
.
А это означает, что при все
элементы
все
элементы ,
а поэтому последовательность
,
а поэтому последовательность имеет
смысл с номераN.
Пусть
имеет
смысл с номераN.
Пусть  -
любое положительное число. Для
числа
-
любое положительное число. Для
числа можно
указать номер
можно
указать номер такой,
что дляn
такой,
что дляn Nвыполняется
Nвыполняется  .
Это и означает, что
.
Это и означает, что –
бесконечно малая. Доказательство второй
части теоремы проводится аналогично.
–
бесконечно малая. Доказательство второй
части теоремы проводится аналогично.
Рассмотрим теперь лемму, которая будет использоваться при доказательстве некоторых теорем.
Лемма. Для
того чтобы число а являлось
пределом последовательности  ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы имел
вид
имел
вид ,n=1,2,…,
где
,n=1,2,…,
где  есть
бесконечно малая последовательность.
есть
бесконечно малая последовательность.
Доказательство. Обозначим  .
Условие
.
Условие по
определению предела равносильно тому,
что для любого числа
по
определению предела равносильно тому,
что для любого числа существует
такой номерN,
что для всех номеров
существует
такой номерN,
что для всех номеров  выполняется
неравенство
выполняется
неравенство ,
то есть
,
то есть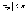 ,
а это и равносильно тому, что
,
а это и равносильно тому, что .
.
Эта лемма показывает особую роль бесконечно малых последовательностей при изучении предела последовательности. Перейдем теперь непосредственно к рассмотрению простейших свойств пределов числовых последовательностей.
