23. Первообразная и неопределенный интеграл. Их свойства.

П. 1. Первообразная и неопределенный интеграл

Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).

Обозначение

где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.

П.2. Свойства неопределенного интеграла

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

24. Первообразная и неопределенный интеграл. Методы вычисления

неопределенных интегралов: интегрирование по частям и замена переменной.

Методы интегрирования.

Интегрирование методом подстановки.

Суть метода заключается в том, что мы вводим новую переменную, выражаем подынтегральную функцию через эту переменную, в результате приходим к табличному (или более простому) виду интеграла.

Очень часто метод подстановки выручает при интегрировании тригонометрических функций и функций с радикалами.

Пример.

Найти неопределенный интеграл .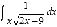

Решение.

Введем новую переменную . Выразим х через z:

Выполняем подстановку полученных выражений в исходный интеграл:

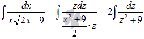
Из таблицы первообразных имеем .

Осталось вернуться к исходной переменной х:

Интегрирование по частям.

Интегрирование по частям основано на представлении подынтегрального выражения в виде произведения и последующем применении формулы . Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.

Пример.

Вычислить неопределенный интеграл .

Решение.

Пусть , тогда

Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.

Теперь применяем формулу интегрирования по частям: 

Последний интеграл вычислим по методу подведения под знак дифференциала.

Так как , то . Поэтому 

Следовательно,   где .

25. Дробно-рациональная функция. Типы простейших алгебраических дробей и их интегрирование.

Дробно-рациональная функция (рациональная дробь) определяется формулой

,

где и– целые числа,,, коэффициенты многочленов – действительные числа,,.

Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя() или неправильной в противном случае ().

Из неправильной рациональной дроби можно "исключить целую часть", т.е. представить неправильную рациональную дробь в виде суммы целой рациональной дроби (многочлена) и правильной рациональной дроби.

1  тип.  — заданные числа 2 тип.  — заданные числа 3 тип. 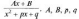— заданные числа Квадратный трехчленне имеет действительных корней. Интегрирование проводится путем выделения полного квадрата в знаменателе:и последующей заменойт.е.   Первый интеграл при помощи заменыприводится к табличному (ОК № 15, формула 2), второй является табличным (формула 15). Пример: 4 тип.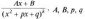— заданные числане имеет действительных корней. Пусть знаменатель правильной рациональной дроби может быть представлен в виде(множителей видаможет быть несколько), где— заданные числа  трехчленне имеет действительных корней. Тогдапредставляется в виде суммы простейших дробей 1—3 типов:   где— неизвестные коэффициенты, которые находятся путем приведения суммы справа к общему знаменателю и последующего приравнивания полученного числителя к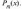Доказательство представлено в [3.С.354]. Примеры: 1) 2) 3) Два метода нахождения коэффициентов в разложении рассмотрим на примере. Пример: Поскольку(см. пример в п. 16.1.1), то Правильную рациональную дробь под интегралом представим в виде суммы простейших:  (16.1) Первый метод — метод неопределенных коэффициентов — заключается в приравнивании коэффициентов при одинаковых степенях х в (16.1): Второй метод — метод частных значений — заключается в подстановке значений х в (16.1), в первую очередь, корней знаменателя: Окончательно имеем