Квадратичные формы

Квадратичной формойf(х₁, х₂,...,х_n) от n переменных называют сумму, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятым с некоторым коэффициентом:f(х₁, х₂,...,х_n) =(a_ij=a_ji).

Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы. Это всегда симметрическаяматрица (т.е. матрица, симметричная относительно главной диагонали,a_ij=a_ji).

В матричной записи квадратичная форма имеет вид f(Х) = Х^ТAX, где

. В самом деле

Например, запишем в матричном виде квадратичную форму .

Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы - половинам соответствующих коэффициентов квадратичной формы. Поэтому

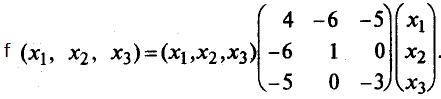
Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С - невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = Х^TАХ = (CY)^TA(CY) = (Y^TC^T)A(CY) =Y^T(C^TAC)Y.

Таким образом, при невырожденном линейном преобразовании С матрица квадратичной формы принимает вид: А^*=C^TAC.

Например, найдем квадратичную форму f(y₁, y₂), полученную из квадратичной формыf(х₁, х₂) = 2x₁²+ 4х₁х₂- 3х₂²линейным преобразованием .

Квадратичная форма называется канонической(имеетканонический вид), если все ее коэффициентыa_ij= 0 приi≠j, т.е.f(х₁, х₂,...,х_n) =a₁₁x₁²+a₂₂x₂² + … +a_nnx_n²=.

Ее матрица является диагональной.

Теорема(доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования.

Например, приведем к каноническому виду квадратичную форму f(х₁, х₂, х₃) = 2x₁²+ 4х₁х₂- 3х₂²– х₂х₃.

Для этого вначале выделим полный квадрат при переменной х₁:

f(х₁, х₂, х₃) = 2(x₁²+ 2х₁х₂+ х₂²) - 2х₂²- 3х₂²– х₂х₃= 2(x₁+ х₂)²- 5х₂²– х₂х₃.

Теперь выделяем полный квадрат при переменной х₂:

f(х₁, х₂, х₃) = 2(x₁+ х₂)²– 5(х₂²– 2* х₂*(1/10)х₃+ (1/100)х₃²) - (5/100)х₃²= = 2(x₁+ х₂)²– 5(х₂– (1/10)х₃)²- (1/20)х₃².

Тогда невырожденное линейное преобразование y₁= x₁+ х₂,y₂= х₂– (1/10)х₃и y₃= x₃приводит данную квадратичную форму к каноническому видуf(y₁,y₂,y₃) = 2y₁²- 5y₂²- (1/20)y₃².

Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами¹). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называютзаконом инерции квадратичных форм.

Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х₂:f(х₁, х₂, х₃) = 2x₁²+ 4х₁х₂- 3х₂²– х₂х₃= -3х₂²– х₂х₃+ 4х₁х₂+ 2x₁²= -3(х₂²– - 2* х₂((1/6) х₃+ (2/3)х₁) +((1/6) х₃+ (2/3)х₁) ²) – 3((1/6) х₃+ (2/3)х₁) ²+ 2x₁²= = -3(х₂– (1/6) х₃- (2/3)х₁)²– 3((1/6) х₃+ (2/3)х₁)²+ 2x₁²=f(y₁,y₂,y₃) = -3y₁²- -3y₂²+ 2y₃², гдеy₁= - (2/3)х₁+ х₂– (1/6) х₃,y₂= (2/3)х₁+ (1/6) х₃и y₃= x₁. Здесь положительный коэффициент 2 приy₃и два отрицательных коэффициента (-3) приy₁иy₂(а при использовании другого способа мы получили положительный коэффициент 2 приy₁и два отрицательных – (-5) приy₂и (-1/20) приy₃).

Также следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.

Квадратичную форму f(X) называютположительно(отрицательно)определенной, если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е.f(X) > 0 (отрицательна, т.е.f(X) < 0).

Например, квадратичная форма f₁(X) = x₁²+ х₂²- положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная формаf₂(X) = -x₁²+ 2x₁х₂- х₂²- отрицательно определенная, т.к. представляет ее можно представить в видеf₂(X) = -(x₁- х₂)².

В большинстве практических ситуации установить знакоопределенность квадратичной формы несколько сложнее, поэтому для этого используют одну из следующих теорем (сформулируем их без доказательств).

Теорема. Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все собственные значения ее матрицы положительны (отрицательны).

Теорема (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры матрицы этой формы положительны.

Главным (угловым) миноромk-го порядка матрицы Аn-го порядка называют определитель матрицы, составленный из первыхkстрок и столбцов матрицы А ().

Отметим, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, причем минор первого порядка должен быть отрицательным.

Например, исследуем на знакоопределенность квадратичную форму f(х₁, х₂) = 2x₁²+ 4х₁х₂+ 3х₂².

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (2 -)* *(3 -) – 4 = (6 - 2- 3+²) – 4 =²- 5+ 2 = 0;D= 25 – 8 = 17;. Следовательно, квадратичная форма – положительно определенная.

Способ 2. Главный минор первого порядка матрицы А ₁=a₁₁= 2 > 0. Главный минор второго порядка₂== 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – положительно определенная.

Исследуем на знакоопределенность другую квадратичную форму, f(х₁, х₂) = -2x₁²+ 4х₁х₂- 3х₂².

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (-2 -)* *(-3 -) – 4 = (6 + 2+ 3+²) – 4 =²+ 5+ 2 = 0;D= 25 – 8 = 17;. Следовательно, квадратичная форма – отрицательно определенная.

Способ 2. Главный минор первого порядка матрицы А ₁=a₁₁= = -2 < 0. Главный минор второго порядка₂== 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – отрицательно определенная (знаки главных миноров чередуются, начиная с минуса).

И в качестве еще одного примера исследуем на знакоопределенность квадратичную форму f(х₁, х₂) = 2x₁²+ 4х₁х₂- 3х₂².

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (2 -)* *(-3 -) – 4 = (-6 - 2+ 3+²) – 4 =²+- 10 = 0;D= 1 + 40 = 41;. Одно из этих чисел отрицательно, а другое – положительно. Знаки собственных значений разные. Следовательно, квадратичная форма не может быть ни отрицательно, ни положительно определенной, т.е. эта квадратичная форма не является знакоопределенной (может принимать значения любого знака).

Способ 2. Главный минор первого порядка матрицы А ₁=a₁₁= 2 > 0. Главный минор второго порядка₂== -6 – 4 = -10 < 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).